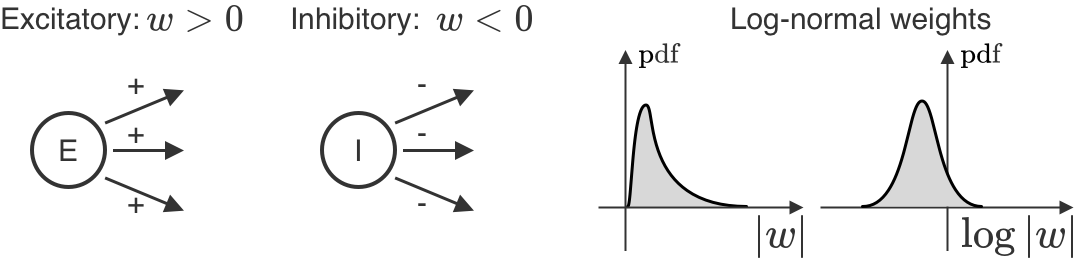
Contrairement à l’intelligence artificielle (IA), nous ne connaissons pas les règles d’apprentissage employées par le cerveau. Cependant, nous en savons beaucoup sur les propriétés neuronales qui dépendent des règles d’apprentissage. Nous nous concentrons ici sur l’une de ces propriétés : la distribution des coefficients synaptiques, c’est-à-dire la distribution des connexions entre les paires de neurones. Pour les neurones biologiques individuels, tous les coefficients sortants sont du même signe : soit positif (excitateur), soit négatif (inhibiteur). En outre, ils ne changent pas de signe au cours de l’apprentissage. Pour l’ensemble des neurones, ces coefficients sont également log-normaux, ce qui signifie que si l’on prend le logarithme des coefficients et que l’on trace un histogramme, celui-ci aura l’air gaussien. Il est important de noter que les modèles d’IA ne font jamais état de l’une ou l’autre de ces observations. Nous montrons que ces faits peuvent à eux seuls nous en apprendre beaucoup sur les règles d’apprentissage que notre cerveau pourrait employer – et sur la manière dont il diffère de l’apprentissage en IA.
Introduction
L’une des façons d’envisager l’apprentissage dans le cerveau est de le comparer à l’apprentissage de type IA : pour s’améliorer dans une tâche, il faut modifier la façon dont on traite les intrants pertinents en changeant les paramètres du réseau, c.-à-d. les coefficients synaptiques. En IA, cela suppose de choisir une fonction de perte qui quantifie la faiblesse de votre performance, puis de suivre l’anti-gradient de cette fonction de perte pour réduire de plus en plus la perte. En IA, cela se fait généralement par descente de gradient sur les paramètres du réseau, ou par rétropropagation. Si nous prenions cette idée au pied de la lettre, nous dirions que le cerveau devrait se contenter de faire de la rétropropagation. Mais il ne faut pas le prendre dans son sens littéral : de nombreuses caractéristiques de l’algorithme de rétropropagation ne sont pas très cohérentes avec le cerveau. De plus, « suivre l’anti-gradient » est cohérent avec une multitude d’algorithmes – en fin de compte, il suffit de s’améliorer dans la tâche à accomplir. Pour déterminer quels algorithmes d’apprentissage sont les plus cohérents avec le cerveau, nous nous concentrons sur l’approche de la descente en miroir – une généralisation de la descente de gradient – et nous montrons que différentes instances de descente en miroir sont liées à différentes distributions des coefficients synaptiques. Dans le cerveau, les distributions des coefficients synaptiques sont très limitées : les neurones ont soit uniquement des coefficients positifs (excitateurs), soit uniquement des coefficients négatifs (inhibiteurs), et les coefficients sont distribués de manière log-normale (voir la figure). Nous montrons qu’un type particulier de descente en miroir, appelé gradient exponentiel, satisfait à ces deux contraintes de coefficients.
Méthodologie
Nous voulons établir un lien entre ce que nous observons dans le cerveau – la séparation excitateur/inhibiteur (E/I) et les coefficients log-normaux – et les mécanismes d’apprentissage. Notre idée centrale est la « géométrie synaptique », c.-à-d. ce qui constitue un grand ou un petit changement. Dans le cas de la descente de gradient, nous disposons d’une méthode très intuitive pour mesurer les changements : il suffit de tracer une ligne droite entre un ensemble de coefficients et un autre, et de dire qu’une ligne plus courte correspond à un changement moins important. Toutefois, certains petits changements sont impossibles dans le cerveau : une minuscule synapse excitatrice ne pourrait pas se transformer en une minuscule synapse inhibitrice. La « géométrie synaptique » du cerveau devrait donc considérer ces changements comme infiniment grands et tenir compte des distributions log-normales.
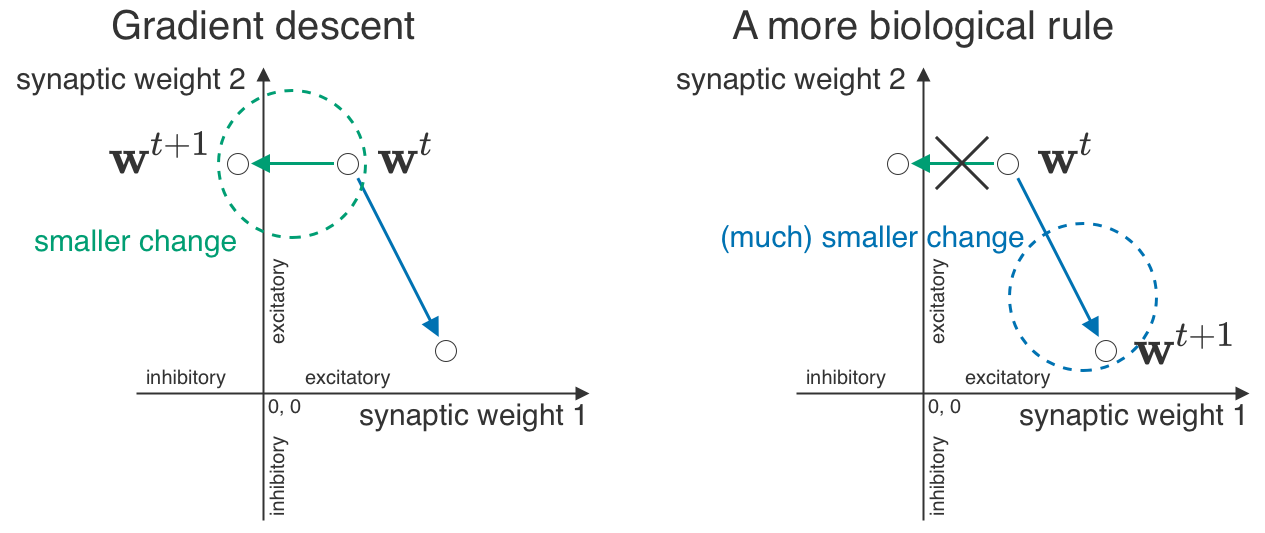
Revenons un instant (mais pas trop longtemps!) à la descente de gradient. Son idée maîtresse est simple : les gradients vous indiquent la direction de la croissance la plus rapide, de sorte que si vous allez dans la direction opposée (anti-gradient), vous pouvez réduire au minimum votre fonction de perte. Mais vous n’êtes pas contraint de vous contenter d’ajouter l’anti-gradient à vos paramètres – vous pouvez trouver des façons plus créatives de l’appliquer.
L’approche de la descente en miroir vous offre un moyen fondé sur des principes de choisir ces moyens créatifs (introduits à l’origine par Nemirovskij et Yudin en 1983 [1]; très bien expliqué dans [2, chapitre 4]). En bref, vous avez besoin de deux éléments : le gradient et une carte entre les paramètres (c.-à-d. les poids synaptiques) – l’espace primal – et un autre espace, l’espace dual. Par exemple, si tous vos coefficients sont positifs, le logarithme pourrait être l’une de ces cartes. Ensuite, dans la descente de gradient, vous ajoutez l’anti-gradient à vos paramètres dans l’espace primal. Dans la descente en miroir, vous faites la même chose, mais dans l’espace dual. Après avoir ajouté l’anti-gradient, nous retransformons le nouveau coefficient dual dans l’espace primal où fonctionne votre réseau (voir la figure). Mais à quoi bon? Cela fonctionne mieux pour certains problèmes. Cela peut même mieux fonctionner pour les réseaux profonds [3]!
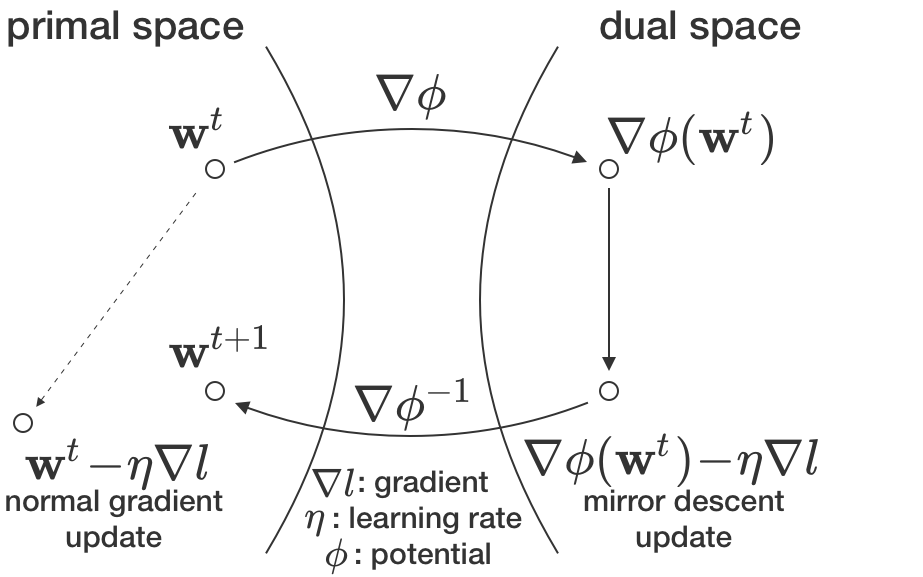
Dans le cas qui nous concerne, la carte utilisée dans la descente en miroir est ce qui rend formelle l’idée quelque peu abstraite de la géométrie synaptique. Soyons encore plus précis : si vous avez des coefficients positifs, vous pouvez prendre le logarithme de ces coefficients (pour passer à l’espace dual), appliquer le gradient dans l’espace logarithmique, puis prendre l’exposant du résultat (pour revenir à l’espace primal). Cet algorithme est connu sous le nom de gradient exponentiel [4], et 1) il maintient les coefficients positifs et 2) il conduit à des distributions de coefficients log-normales. La première propriété est toujours valable; la seconde implique une sorte de comportement de type théorème central limite des changements dans l’espace logarithmique. Nous démontrons que pour un apprentissage de type régression linéaire (p. ex., le régime NTK [5] ou l’affinage), le changement total dans l’espace logarithmique semble en effet gaussien. Cela implique des coefficients finaux log-normaux lorsque les coefficients initiaux sont également log-normaux. D’autres cartes affichent le même comportement, mais dans un espace différent de coefficients transformés.
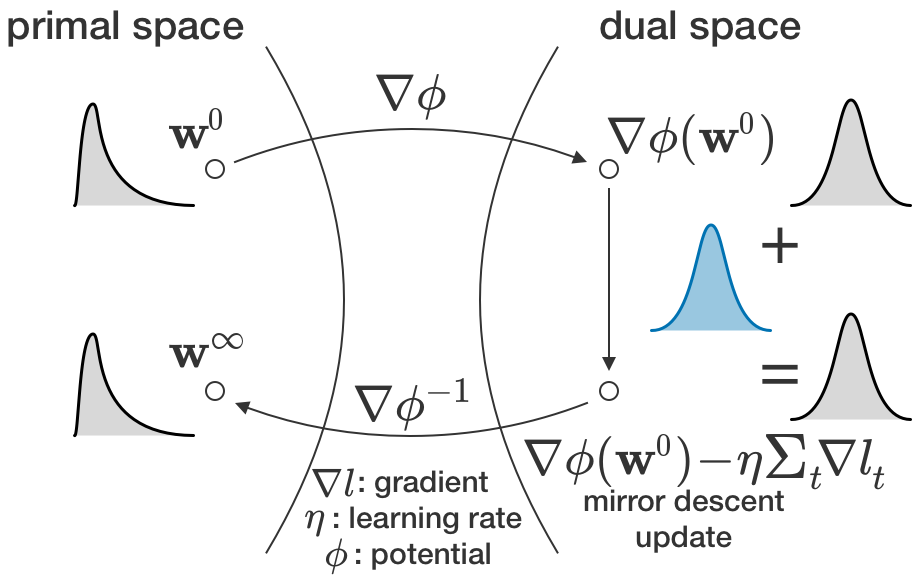
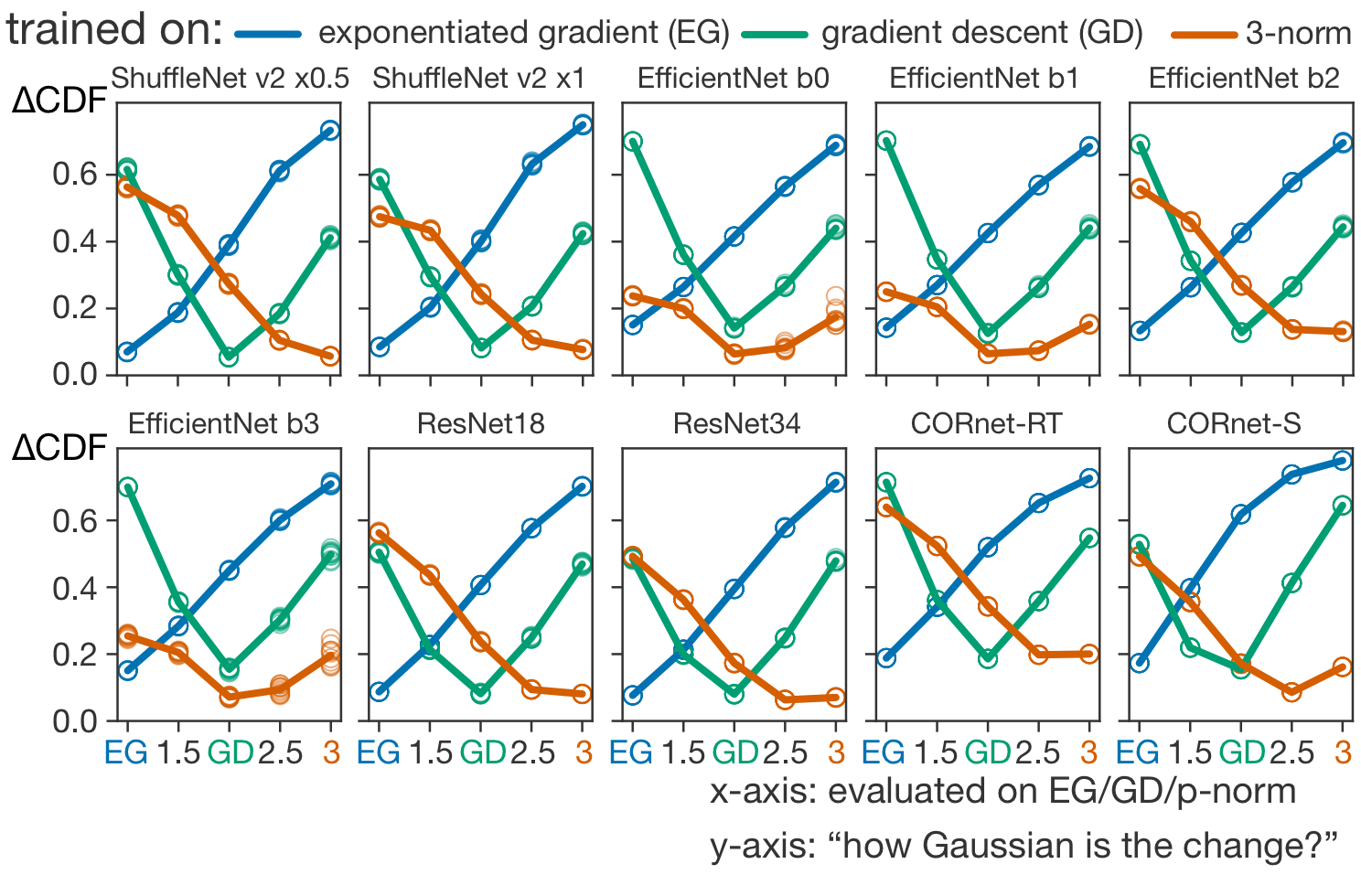
Si nous connaissons les coefficients initiaux et les coefficients finaux, pour la bonne carte, le changement aura l’air gaussien. Dans le cas d’une carte erronée, ce n’est pas le cas. Nous pouvons donc déterminer quelle carte a été utilisée pour l’apprentissage en fonction du caractère gaussien des changements. Nous ne disposons pas (encore) de telles données pour le cerveau, mais nous pouvons tout de même mettre notre théorie à l’épreuve avec les réseaux profonds. (Remarque importante : il est essentiel d’examiner les changements liés à l’apprentissage plutôt que les coefficients finaux. La log-normalité ne doit pas découler du tout de l’apprentissage). Nous avons utilisé des réseaux profonds pré-entraînés et les avons affinés à l’aide de différentes cartes pour voir si nous pouvons correctement deviner la « véritable cartographie » à partir du caractère gaussien des changements de coefficients. Il s’avère que c’est possible, même pour les réseaux récurrents (CORnets [6], dans la figure ci-dessous) – et de manière plus fiable pour l’algorithme du gradient exponentiel qui, comme nous l’avons vu plus haut, préserve la séparation E/I et la log-normalité.
Conclusion
Dans cet article, nous avons établi un lien entre les distributions des coefficients synaptiques et les algorithmes d’apprentissage sous-jacents. Plus précisément, nous avons montré que différentes instances du cadre de la descente en miroir produisent des distributions de coefficients différentes, et que les distributions log-normales observées de manière expérimentale sont cohérentes avec l’algorithme du gradient exponentiel.
Nous avons déjà fait allusion au besoin d’expériences supplémentaires pour mettre à l’épreuve cette théorie. Nous devons savoir comment chaque coefficient synaptique change. Nous avons également vu qu’aller au-delà de la descente de gradient pourrait s’avérer une bonne idée en IA [3]. Mais qu’est-ce que cela signifie pour l’intégration de l’IA aux neurosciences?
Même si une règle d’apprentissage (pour simplifier, la descente de gradient/rétropropagation) n’est pas compatible avec des coefficients log-normaux, elle partage la plupart de la « machinerie », c’est-à-dire le calcul du gradient entre les neurones, avec la version exponentielle de la même règle. Ce qui, à son tour, est compatible avec la log-normalité et devrait également fonctionner correctement pour l’apprentissage. Bien que notre théorie soit développée pour la rétropropagation (ou ses approximations), l’idée générale des changements d’apparence gaussienne peut s’appliquer à d’autres règles d’apprentissage. Après tout, si nous additionnons les mises à jour de coefficients dans un certain espace, elles y auront une apparence gaussienne, et c’est tout ce dont nous avons besoin.
Publié en tant que "conference paper" à ICLR 2024 : https://arxiv.org/pdf/2305.19394.pdf
Références
[1] Arkadij Semenovič Nemirovskij and David Borisovich Yudin. Problem complexity and method
efficiency in optimization. Wiley-Interscience, 1983.
[2] Sébastien Bubeck, Convex optimization: Algorithms and complexity, Foundations and Trends® in Machine Learning, 2015.
[3] Haoyuan Sun, Khashayar Gatmiry, Kwangjun Ahn, and Navid Azizan, A Unified Approach to Controlling Implicit Regularization via Mirror Descent, Journal of Machine Learning Research, 2023.
[4] Jyrki Kivinen and Manfred K Warmuth, Exponentiated gradient versus gradient descent for linear
predictors, Information and Computation, 1997.
[5] Arthur Jacot, Franck Gabriel, and Clément Hongler, Neural tangent kernel: Convergence and generalization in neural networks, Advances in Neural Information Processing Systems, 2018.
[6] Jonas Kubilius, Martin Schrimpf, Ha Hong, Najib J. Majaj, Rishi Rajalingham, Elias B. Issa, Kohitij
Kar, Pouya Bashivan, Jonathan Prescott-Roy, Kailyn Schmidt, Aran Nayebi, Daniel Bear, Daniel
L. K. Yamins, and James J. DiCarlo, Brain-Like Object Recognition with High-Performing Shal-
low Recurrent ANNs, Advances in Neural Information Processing Systems, 2019