Unlike in AI, we do not know which learning rules are used by the brain. However, we know a lot about neural properties that depend on the learning rule. Here we focus on one of these properties – the distribution of synaptic weights, i.e. the distribution of the connections between pairs of neurons. For individual biological neurons, all of their outgoing weights are of the same sign: either positive (excitatory), or negative (inhibitory). Moreover, they do not change signs over learning. Across neurons, these weights are also log-normal, meaning that if we take the logarithm of the weights and plot a histogram, it would look Gaussian. Importantly, we never see either of these observations in AI models. We show that these facts alone can tell us a lot about the learning rules our brain might employ – and how it differs from learning in AI.
Introduction
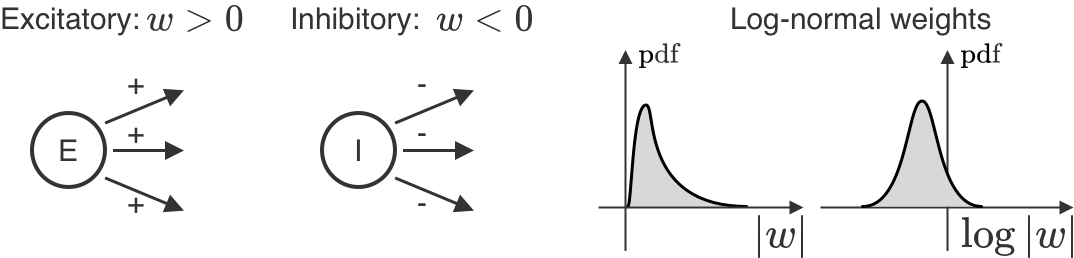
One way to think about learning in the brain is by comparison to AI-style learning: to get better at a task you need to change how you process task-relevant inputs – by changing network parameters, i.e. synaptic weights. In AI, this means choosing a loss function that quantifies how badly you are performing, and then following the anti-gradient of that loss function to make the loss smaller and smaller. In AI, this is usually done via gradient descent over network parameters, or backprop. If we took this idea literally, we’d say the brain should just do backprop. But we shouldn’t take it literally: many features of backprop as an algorithm are not very consistent with the brain, and moreover “following the anti-gradient” is consistent with a plethora of algorithms – in the end, you just need to improve on the task. To study what learning algorithms are more consistent with the brain, we concentrate on the mirror descent framework – a generalization of gradient descent – and show that different instances of mirror descent are linked to different synaptic weight distributions. In the brain, synaptic weight distributions are very constrained: neurons have either only positive (excitatory) or only negative (inhibitory) weights, and the weights are distributed log-normally (see the figure). We show that one specific instance of mirror descent, called exponentiated gradient, satisfies both of these weight constraints.
Development
We want to connect what we observe in the brain – the excitatory/inhibitory (E/I) separation and log-normal weights – to learning mechanisms. Our core idea is “synaptic geometry”, i.e. what constitutes a large vs. small change. For gradient descent, we have a very intuitive way to measure changes: take a straight line from one set of weights to another one, and say that a shorter line corresponds to a smaller change. But in the brain, some small changes are impossible – a tiny excitatory synapse wouldn’t be able to become a tiny inhibitory one. So the “synaptic geometry” of the brain should treat those changes as infinitely large, and also somehow account for the log-normal distributions.
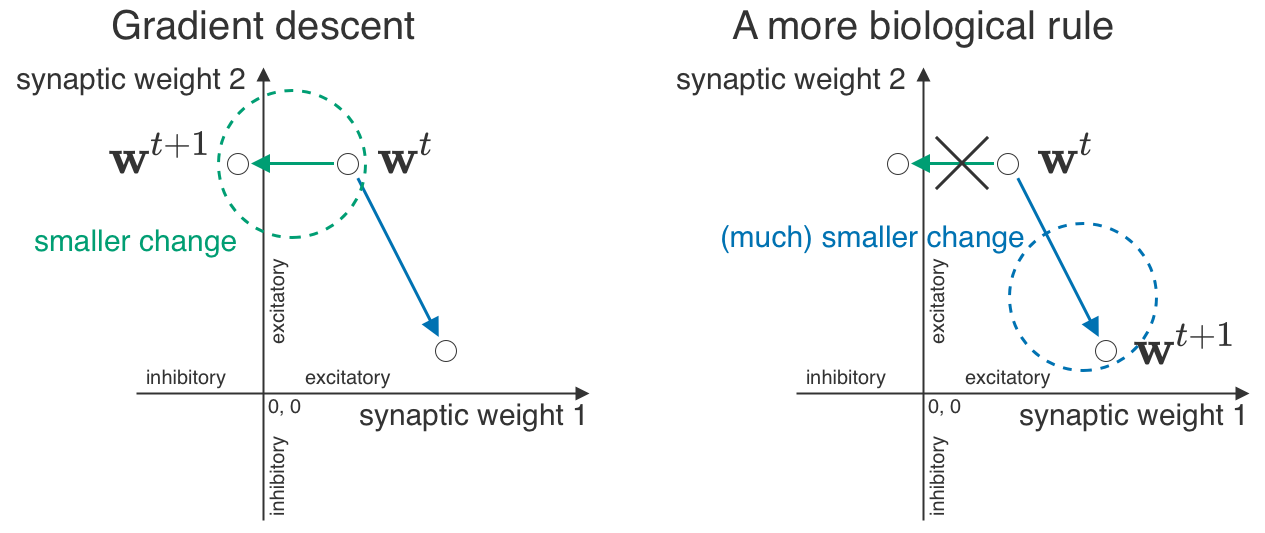
Let’s go back to gradient descent for a moment (but not for long!). Its core idea is simple: gradients tell you the direction of fastest growth, so if you go in the opposite direction (anti-gradient), you can minimize your loss function. But you don’t have to just add the anti-gradient to your parameters – you can find more creative ways to apply it.
The mirror descent framework gives you a principled way to choose those creative ways (originally introduced by Nemirovskij & Yudin in 1983 [1]; very well explained in [2, Chapter 4]). Briefly, you need two components: the gradient and a map between the parameters (i.e. synaptic weights) – the primal space – and some other dual space. For instance, if all your weights are positive, the logarithm could be one such map. Moving on, in gradient descent, you add the anti-gradient to your parameters in the primal space. In mirror descent, you do the same thing – but in the dual space. After adding the anti-gradient, we transform the new dual weight back to the primal space where your network operates (see the figure). But why bother? It works better for some problems. It can even work better for deep networks [3]!
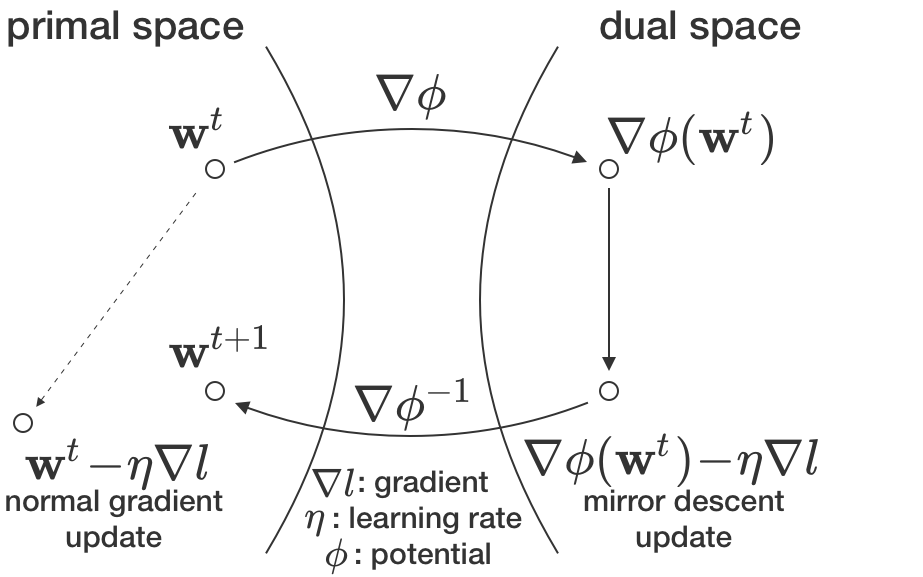
In our case, the map used in mirror descent is what makes the somewhat abstract idea of synaptic geometry formal. Let’s be even more specific: if you have positive weights, you can take the log of those weights (thus moving to the dual space), apply the gradient in the log space, and then take the exponent of the result (to move back to the primal space). This algorithm is known as exponentiated gradient [4], and it (1) keeps positive weights positive and (2) leads to log-normal weight distributions. The first property always holds; the second implies some sort of central limit theorem-style behavior of changes in the log space. We show that for linear regression-like learning (e.g. the NTK regime [5] or finetuning), the total change in the log space would indeed look Gaussian. This implies log-normal final weights when the initial are also log-normal. Other mappings show the same behavior, but in a different space of transformed weights.
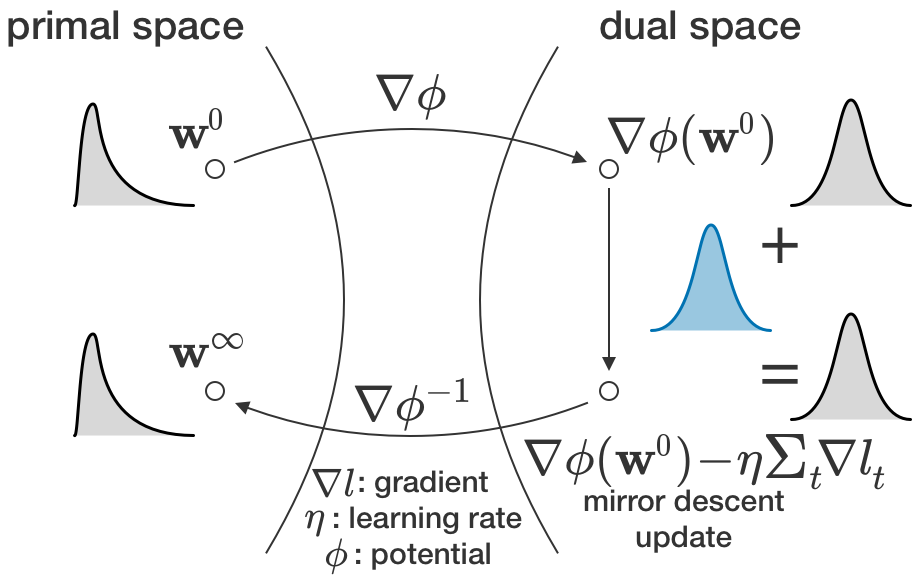
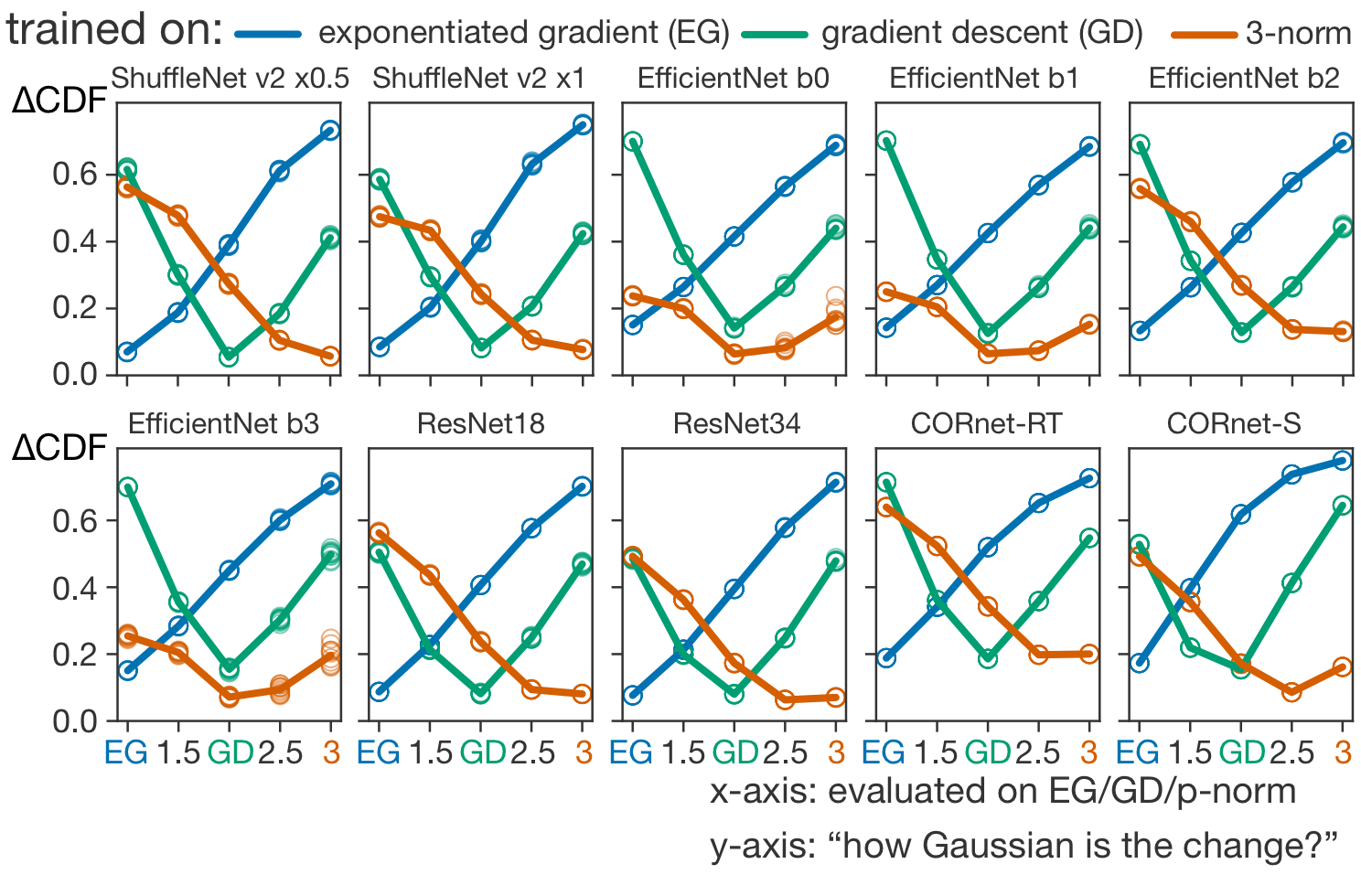
If we know the initial weights and the final weights, for the right map the change will look Gaussian. For a wrong one, it won’t, so we can determine what map was used for training based on how Gaussian the changes are. We don’t have such data for the brain (yet), but we can still test our theory with deep networks. (An important note: looking at learning-driven changes rather than just final weights is crucial. Log-normality doesn’t have to follow from learning at all.) We took pre-trained deep networks, and finetuned them with different maps to see if we can correctly guess the “true mapping” from Gaussianity of weight changes. Turns out that we can, even for recurrent networks (CORnets [6] on the plot) – and most reliably for the exponentiated gradient algorithm that, as we’ve discussed above, preserves the E/I separation and log-normality.
Conclusion
In this work, we connected synaptic weight distributions to the underlying learning algorithms. Specifically, we showed that different instances of the mirror descent framework produce different weight distributions, and the experimentally observed log-normal distributions are consistent with the exponentiated gradient algorithm.
We’ve already hinted at the need for more experiments to test this theory – we need to know how every synaptic weight changes; we’ve also seen that going beyond gradient descent might be a good idea in AI [3]. But what does it mean for NeuroAI?
Even if a learning rule (for simplicity, gradient descent/backprop) is not consistent with log-normal weights, it shares most of the “machinery”, i.e. gradient computation across neurons, with the exponentiated version of the same rule. Which, in turn, is consistent with log-normality, and is also expected to work well for learning. While our theory is developed for backprop (or its approximations), the general idea of Gaussian-looking changes might apply to other learning rules – after all, if we sum weight updates in some space, they’ll look somewhat Gaussian there, and that’s all we need.
Paper Link : https://arxiv.org/pdf/2305.19394.pdf
References
[1] Arkadij Semenovič Nemirovskij and David Borisovich Yudin. Problem complexity and method
efficiency in optimization. Wiley-Interscience, 1983.
[2] Sébastien Bubeck, Convex optimization: Algorithms and complexity, Foundations and Trends® in Machine Learning, 2015.
[3] Haoyuan Sun, Khashayar Gatmiry, Kwangjun Ahn, and Navid Azizan, A Unified Approach to Controlling Implicit Regularization via Mirror Descent, Journal of Machine Learning Research, 2023.
[4] Jyrki Kivinen and Manfred K Warmuth, Exponentiated gradient versus gradient descent for linear
predictors, Information and Computation, 1997.
[5] Arthur Jacot, Franck Gabriel, and Clément Hongler, Neural tangent kernel: Convergence and generalization in neural networks, Advances in Neural Information Processing Systems, 2018.
[6] Jonas Kubilius, Martin Schrimpf, Ha Hong, Najib J. Majaj, Rishi Rajalingham, Elias B. Issa, Kohitij
Kar, Pouya Bashivan, Jonathan Prescott-Roy, Kailyn Schmidt, Aran Nayebi, Daniel Bear, Daniel
L. K. Yamins, and James J. DiCarlo, Brain-Like Object Recognition with High-Performing Shal-
low Recurrent ANNs, Advances in Neural Information Processing Systems, 2019