Note de la rédaction : Présenté à ICLR 2022
Le bruit sur des estimations de valeurs utilisées pour superviser l’évaluation et l’optimisation des politiques peut nuire à l’efficience en matière d’échantillons dans le cadre des algorithmes d’apprentissage par renforcement (« reinforcement learning » ou RL) profond sans modèles. Comme ce type de bruit est hétéroscédastique, ses effets peuvent être atténués en utilisant des pondérations basées sur l’incertitude dans le processus d’optimisation. Les méthodes existantes reposent sur des ensembles échantillonnés qui ne saisissent pas tous les aspects de l’incertitude. Nous fournissons une analyse systématique des sources d’incertitude dans la supervision bruitée qui se produit en RL, et nous introduisons le RL à la pondération par l’inverse de la variance – un cadre bayésien qui combine les ensembles probabilistes et la pondération par l’inverse de la variance dans le lot. Nous proposons une méthode par laquelle deux méthodes complémentaires d’estimation de l’incertitude tiennent compte à la fois de l’incertitude de la valeur Q et de la stochasticité de l’environnement pour mieux atténuer les impacts négatifs de la supervision bruitée. Ainsi, nos résultats démontrent une amélioration significative en termes d’efficience en matière d’échantillons sur des tâches de contrôle discrètes et continues.
Bruit hétéroscédastique sur la cible
Pour la majorité des algorithmes du RL profond sans modèle, tels que DQN (Mnih et al., 2013) et SAC (Haarnoja et al., 2018), une politique \( π \) est évaluée en fonction de la paire état-action (\( s,a \)). Pour apprendre à évaluer cette politique, un approximateur de fonction neuronal est entraîné en utilisant la supervision d’une cible \( T \).
Afin d’obtenir cette cible, l’agent enregistre :
- La récompense \( r \) obtenue et ;
- l’état \( s’ \) atteint après avoir effectué l’action \( a \) à l’état \( s \).
- Ensuite, l’agent envisage quelle action \( a’ \) sera fournie par la politique à \( s’ \).
- Il utilise ensuite l’évaluation actuelle (et imparfaite) de la politique pour obtenir la valeur Q à (\(s’,a’\)).
- La cible \( T \) est calculée par l’équation \(T(s,a)=r+\gamma \bar{Q}(s′,a′)\).
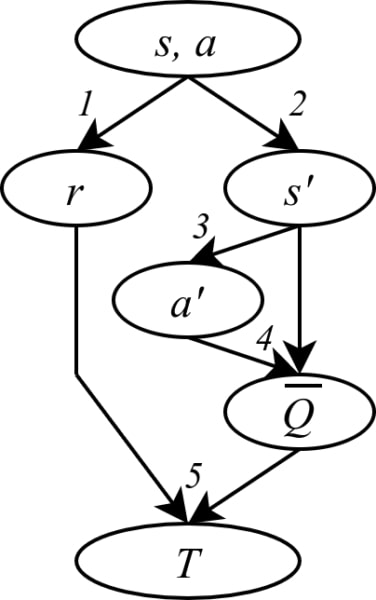
Les étapes 1, 2 et 3 peuvent être stochastiques, et l’étape 4 repose sur l’évaluation actuelle (et incertaine) de la valeur Q. Ces-dernières créent du bruit sur les étiquettes de la tâche de supervision : apprendre à prédire la valeur de la politique. La supervision de données bruitées ralentit le processus d’apprentissage.
L’idée principale derrière ce projet est que le bruit sur la cible est hétéroscédastique, c’est-à-dire qu’il n’est pas toujours échantillonné à partir de la même distribution. Si la variance de cette distribution est connue, il est possible d’atténuer les effets du bruit sur la supervision en appliquant un schéma de pondération qui réduit l’importance des échantillons à haute variance, et donc d’améliorer l’efficience en matière d’échantillons des algorithmes de RL profond.
Les deux principales contributions de l’apprentissage par renforcement à variance inverse (IV-RL) sont donc l’évaluation de la variance de la distribution visée et l’utilisation du schéma de pondération approprié.
Évaluer la variance de la cible
Nous évaluons la variance de la cible de deux manières. Tout d’abord, nous utilisons des réseaux de variance, entraînés en utilisant la fonction de perte de vraisemblance logarithmique négative (NLL).
\( L_{NLL}(x,y,\theta)=\frac{|f(x,\theta)-y|^2}{\sigma^2}+\ln(\sigma^2) \)
En apprentissage supervisé, NLL permet au réseau de prédire la variance des étiquettes pour une entrée donnée. Par exemple, si nous avons plusieurs étiquettes pour la même entrée \((s,a)\), la prédiction du réseau tendra vers \(\mu(s,a)\), la moyenne des étiquettes, et la prédiction de la variance établie par le réseau constitueront la variance de ces étiquettes.
Nous utilisons des réseaux de variance avec NLL pour estimer la variance dans la cible considérant la stochasticité des étapes 1, 2 et 3. Pour mieux comprendre le processus, imaginez pour un instant que la valeur de \(\bar{Q}(s′,a′)\) utilisé sur la cible est toujours la même compte tenu de \((s’, a’)\). Dans ce cas, pour une paire \((s,a)\) donnée, le fait d’avoir différentes cibles \( T \) sera dû au fait d’obtenir différentes valeurs de \(r\), \(s′\) et \(a′\). La variance indiquée par NLL saisit donc l’effet de la stochasticité de la récompense (1), des dynamiques liées à l’environnement (2), et de la politique (3).
Nous souhaitons aussi estimer l’incertitude prédictive de \(\bar{Q}(s′,a′)\) qui est estimée lors de l’étape 4. Cette valeur est bruitée en raison du manque d’expérience. Par exemple, au début du processus d’entraînement, l’estimateur de valeur ne connaît aucunement la valeur réelle de \((s’,a’)\). Ici, nous utilisons des ensembles de variance (Lakshmiranayanan et al., 2016) : au lieu d’un réseau de variance unique, nous entraînons séparément 5 réseaux de variance, avec des conditions initiales et des ensembles d’entraînement qui varient. Chaque réseau prédit une moyenne et une variance pour \(\bar{Q}(s′,a′)\). La variance de \(\bar{Q}(s′,a′)\) est alors obtenue en calculant la variance du mélange gaussien qui en résulte. On considère ici que les réseaux ne convergeront dans leurs prédictions que s’ils ont été suffisamment entraînés sur l’environnement \((s’,a’)\). Sinon, leurs prédictions divergeront, ce qui produira une variance plus élevée.
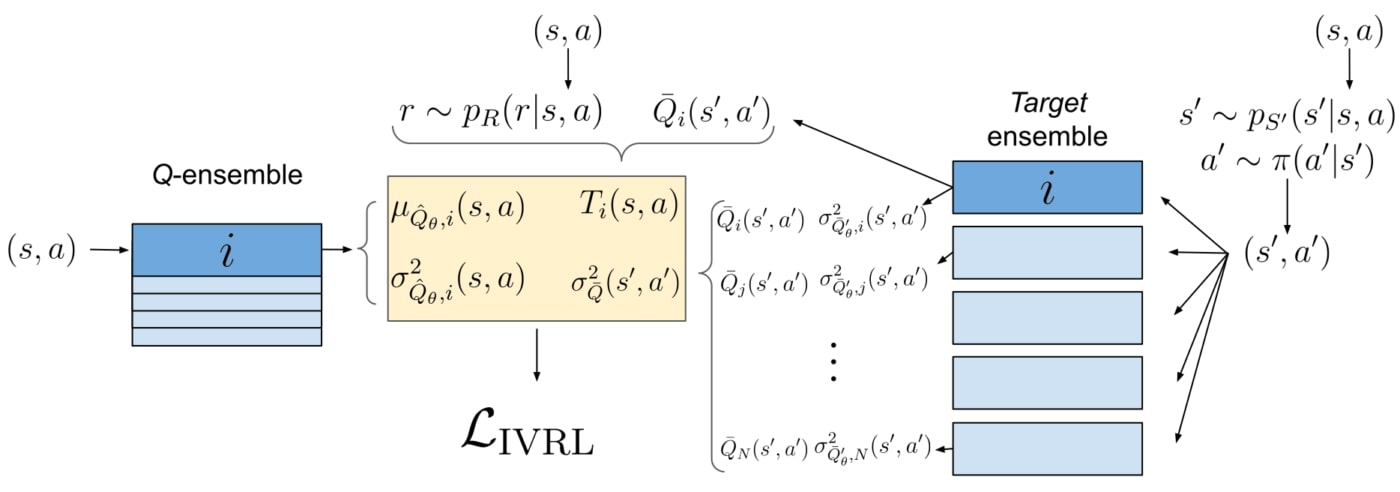
Schéma de pondération et la fonction objectif
Une fois ces deux mesures de variance obtenues pour une même cible, comment pouvons-nous les appliquer pour atténuer l’effet du bruit? Lorsque la variance est connue dans une régression hétéroscédastique, nous pouvons intégrer des poids dans la fonction objectif pour réduire l’impact des étiquettes hautement bruitées tout en augmentant la confiance des étiquettes à faible bruit. Pour la régression linéaire, les poids optimaux sont l’inverse de la variance. Il est plus difficile de prouver qu’ils sont optimaux en ce qui concerne l’optimisation de réseaux neuronaux mais nous pouvons suivre le même principe.
Dans la formulation NLL pour les réseaux de variance, l’erreur est déjà divisée par la variance prédite. Dans notre étude, nous montrons que l’usage simple des réseaux de variance dans l’ensemble mène à des améliorations significatives de l’efficacité de l’échantillon et des performances d’apprentissage.
Pour tenir compte de l’incertitude prédictive, nous utilisons un schéma de pondération appelé Batch Inverse-Variance (BIV) (Mai et al., 2021). Les poids de la variance inverse sont normalisés sur le mini-lot et un hyperparamètre permet de contrôler l’intensité du schéma de pondération à travers la taille effective du lot. Cela permet d’obtenir une certaine robustesse, d’autant plus que les méthodes d’estimation de la variance que nous utilisons ne fonctionnent pas toujours sans heurts : la variance peut être fortement sous-estimée ou surestimée. Nous constatons à nouveau que l’utilisation de BIV avec des ensembles (sans ensembles de variance) améliore l’efficacité de l’échantillon.
Nous combinons les deux dans une fonction multi-objectif, aboutissant à des performances nettement plus efficaces que lorsque l’on ne considère que l’une ou l’autre des prédictions d’incertitude.
Cadre et travaux existants
Nous appliquons l’apprentissage par renforcement à variance inverse (IV-RL) sur DQN et SAC. Cette implémentation nécessite la prise de plusieurs décisions de conception. De plus, les ensembles peuvent également être utilisés pour des stratégies d’exploration tenant compte de l’incertitude, que nous avons utilisées bien que nous ne les ayons pas développées nous-mêmes. Nous construisons notre structure IV-RL en nous basant sur des travaux existants, notamment : BootstrapDQN (Osband et al., 2016), Randomized Prior Functions (Osband et al., 2018) et SUNRISE (Lee et al., 2020). UWAC (Wu et al., 2021) est aussi un article très intéressant dans la même lignée que IV-RL, bien qu’il se penche sur un problème légèrement différent relié à l’apprentissage par renforcement par lots, sous l’angle de la détection d’échantillons hors distribution.
Résultats
IV-RL démontre une amélioration significative de l’efficience en matière d’échantillons et de la performance d’apprentissage lorsqu’appliqué à DQN et SAC, comme le démontre la figure ci-dessous.
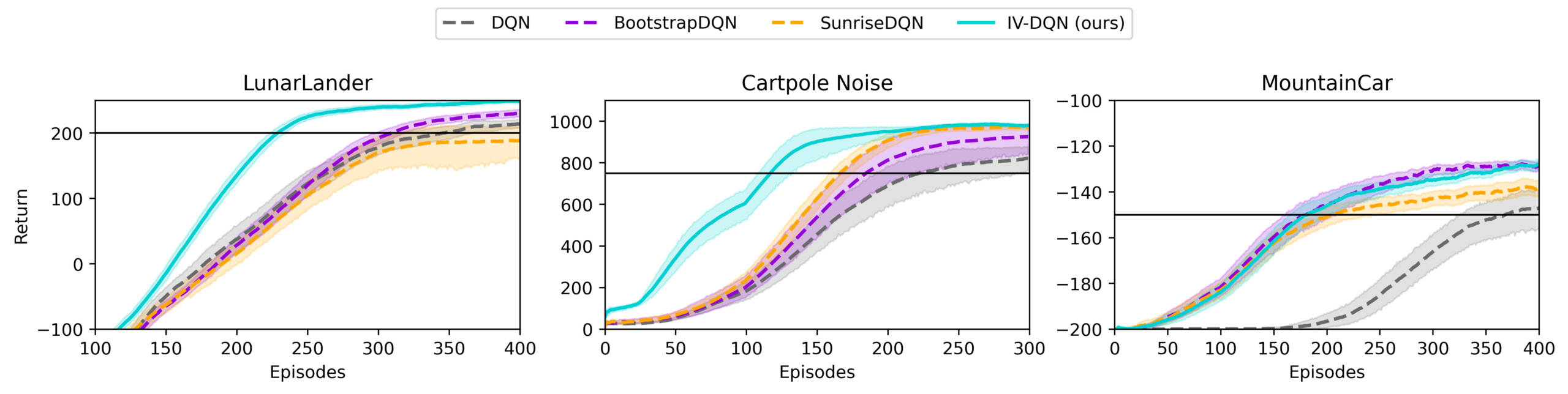
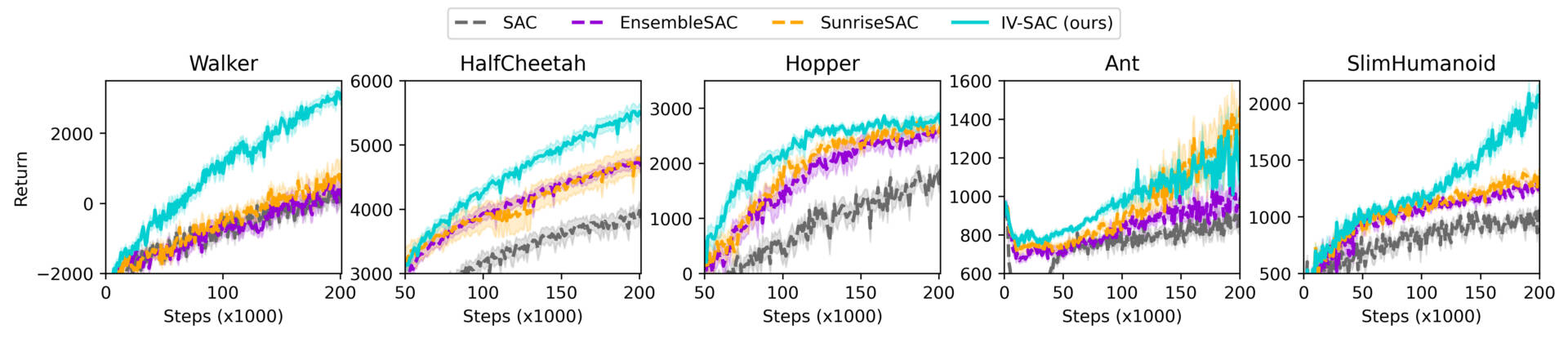
La publication et les contenus additionnels comprennent plus de résultats, y compris des études sur l’ablation, sur l’influence de certains hyperparamètres, des graphiques d’estimation de la variance et les performances d’autres structures et d’autres schémas de pondération.
Signification et perspectives d’avenir
En IV-RL, l’équation de Bellman est observée sous l’angle de la régression bruitée et hétéroscédastique. Cela conduit aux défis de l’estimation de la variance cible et de son utilisation pour réduire l’effet du bruit. Les améliorations significatives démontrées dans les résultats prouvent que cet angle d’analyse est une piste qui pourrait aider le domaine de l’apprentissage par renforcement profond à surmonter le défi de l’efficience en matière d’échantillons.
Ces idées sont difficiles à implémenter. Les techniques d’estimation de variance utilisées en IV-RL sont délicates et capricieuses. Elles sont sujettes à une dynamique d’apprentissage contre-intuitive et l’échelle des variances prédites n’est pas calibrée. Pour les intégrer aux algorithmes IV-RL, nous avons dû entreprendre plusieurs étapes pour solidifier le processus en cas de de surestimation ou sous estimation des valeurs de la variance – parfois, en ajustant le pouvoir discriminant des poids (en utilisant \(\xi\) en BIV), ou en sacrifiant un peu d’efficacité de calcul (en utilisant des ensembles).
De plus, puisque la formulation NLL utilise déjà les pondérations à variance inverse, les deux variances estimées ne peuvent pas être additionnées l’une à l’autre dans une fonction de perte à un seul objectif, ce qui aurait logiquement été le cas en suivant notre analyse théorique. Il pourrait s’agir d’une piste d’amélioration de l’algorithme. IV-RL prouve que le fait de tenir compte de l’incertitude de la cible dans l’équation de Bellman est une avenue très prometteuse pour améliorer l’efficience en matière d’échantillons en apprentissage par renforcement profond. Il s’agit d’un algorithme fonctionnel, efficient au plan de l’échantillonnage, qui peut être utilisé tel quel. C’est aussi une démonstration de principe qui peut être améliorée : nous invitons fortement à entreprendre de nouveaux travaux en ce sens, tout comme à adapter l’idée à d’autres algorithmes et sous domaines de l’apprentissage par renforcement profond.
Publication officielle: https://openreview.net/pdf?id=vrW3tvDfOJQ
ArXiv: https://arxiv.org/abs/2201.01666
Code source sur Github: https://github.com/montrealrobotics/iv_rl
Références
Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Alex Graves, Ioannis Antonoglou, Daan Wierstra, and Martin Riedmiller. Playing Atari with deep reinforcement learning. NIPS, pp. 9, 2013.
Ian Osband, Charles Blundell, Alexander Pritzel, and Benjamin Van Roy. Deep exploration via bootstrapped DQN. arXiv:1602.04621, Jul 2016.
Ian Osband, John Aslanides, and Albin Cassirer. Randomized prior functions for deep reinforcement learning. In Advances in Neural Information Processing Systems, volume 31. Curran Associates, Inc., 2018
Tuomas Haarnoja, Aurick Zhou, Pieter Abbeel, and Sergey Levine. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. arXiv:1801.01290, 2018.
Kimin Lee, Michael Laskin, Aravind Srinivas, and Pieter Abbeel. SUNRISE: A simple unified framework for ensemble learning in deep reinforcement learning. arXiv:2007.04938, Jul 2020.
Yue Wu, Shuangfei Zhai, Nitish Srivastava, Joshua Susskind, Jian Zhang, Ruslan Salakhutdinov, and Hanlin Goh. Uncertainty weighted actor-critic for offline reinforcement learning. arXiv:2105.08140, May 2021.
Vincent Mai, Waleed Khamies, and Liam Paull. Batch inverse-variance weighting: Deep heteroscedastic regression. arXiv:2107.04497, Jul 2021.