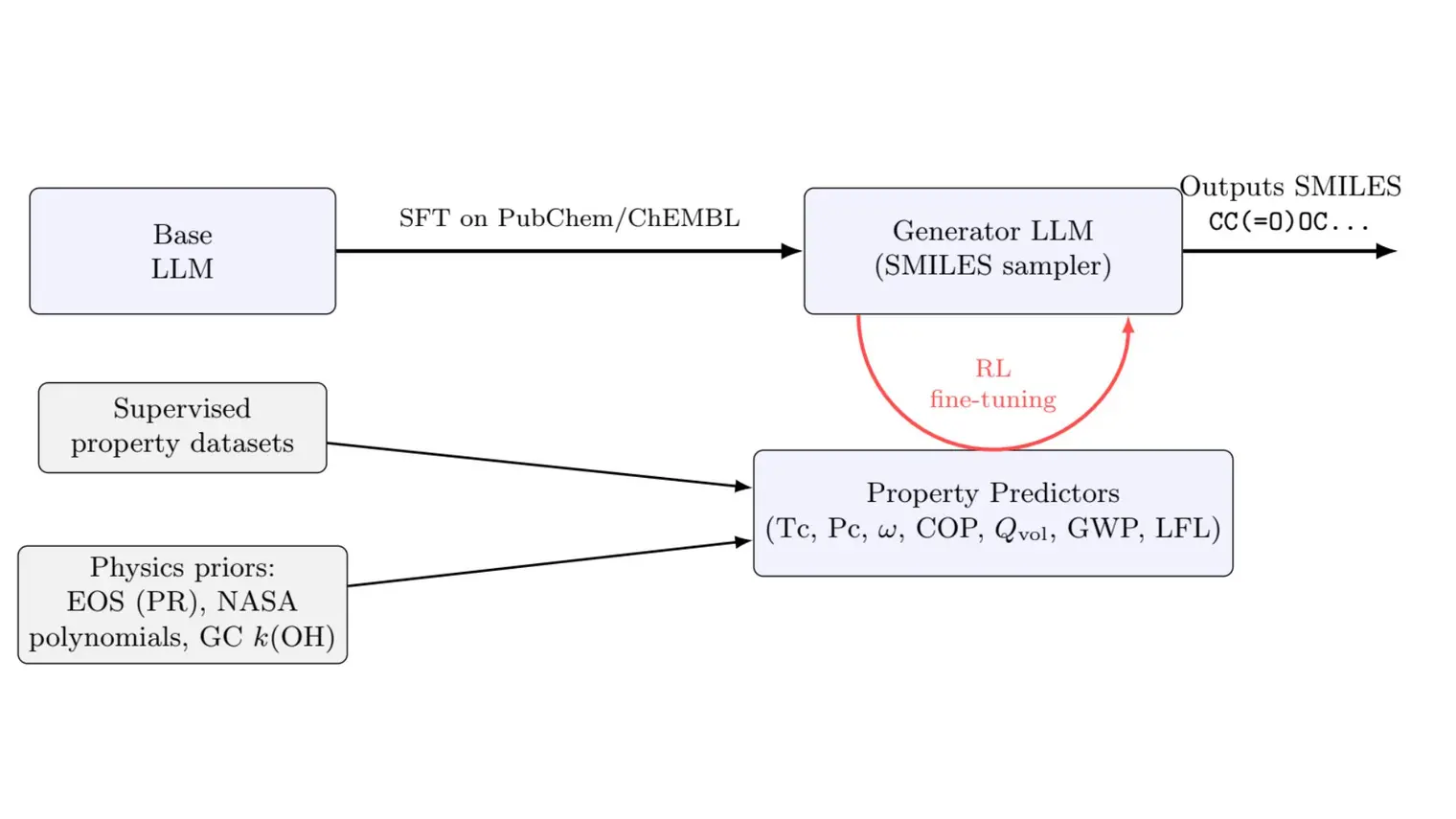
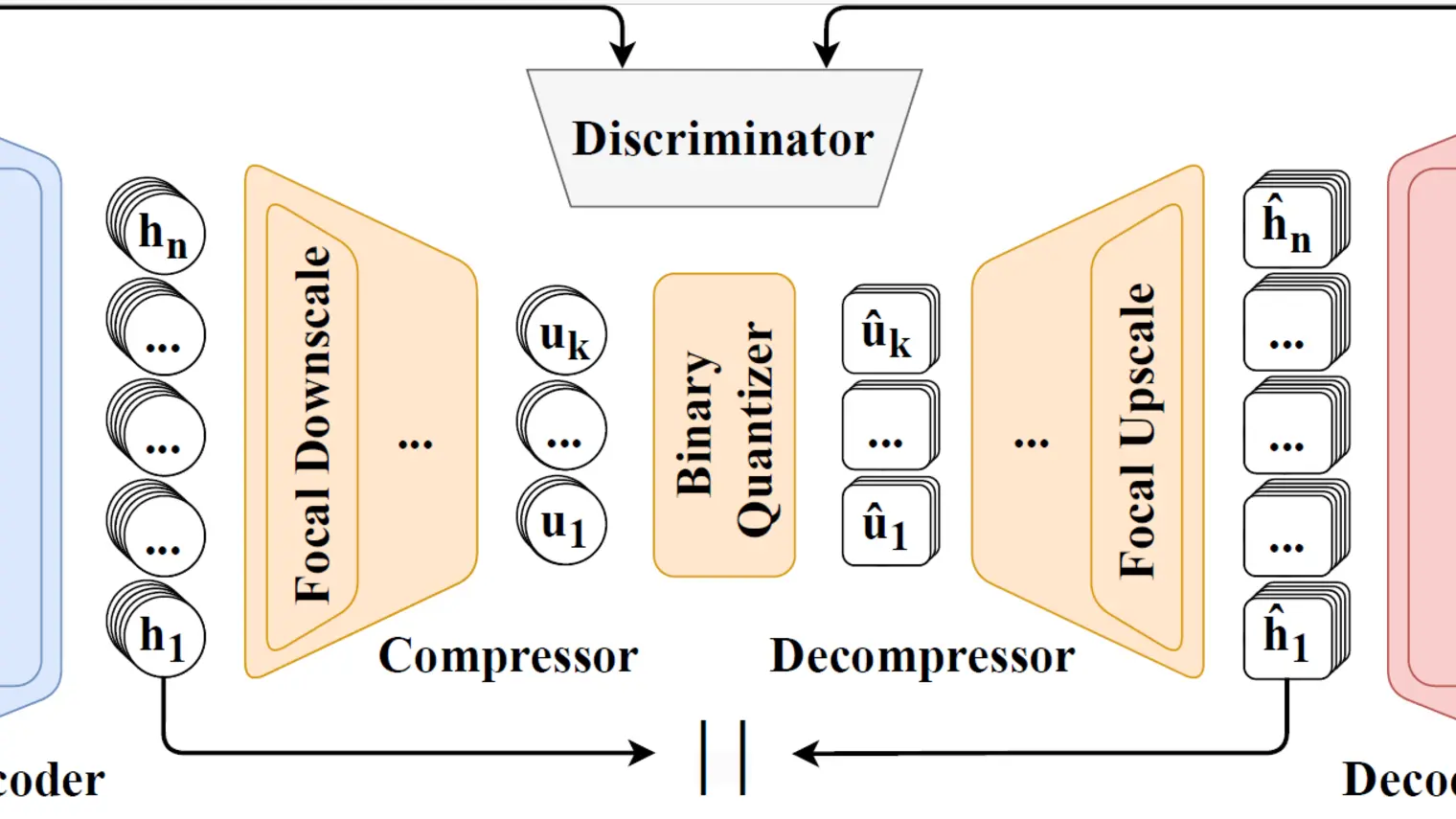
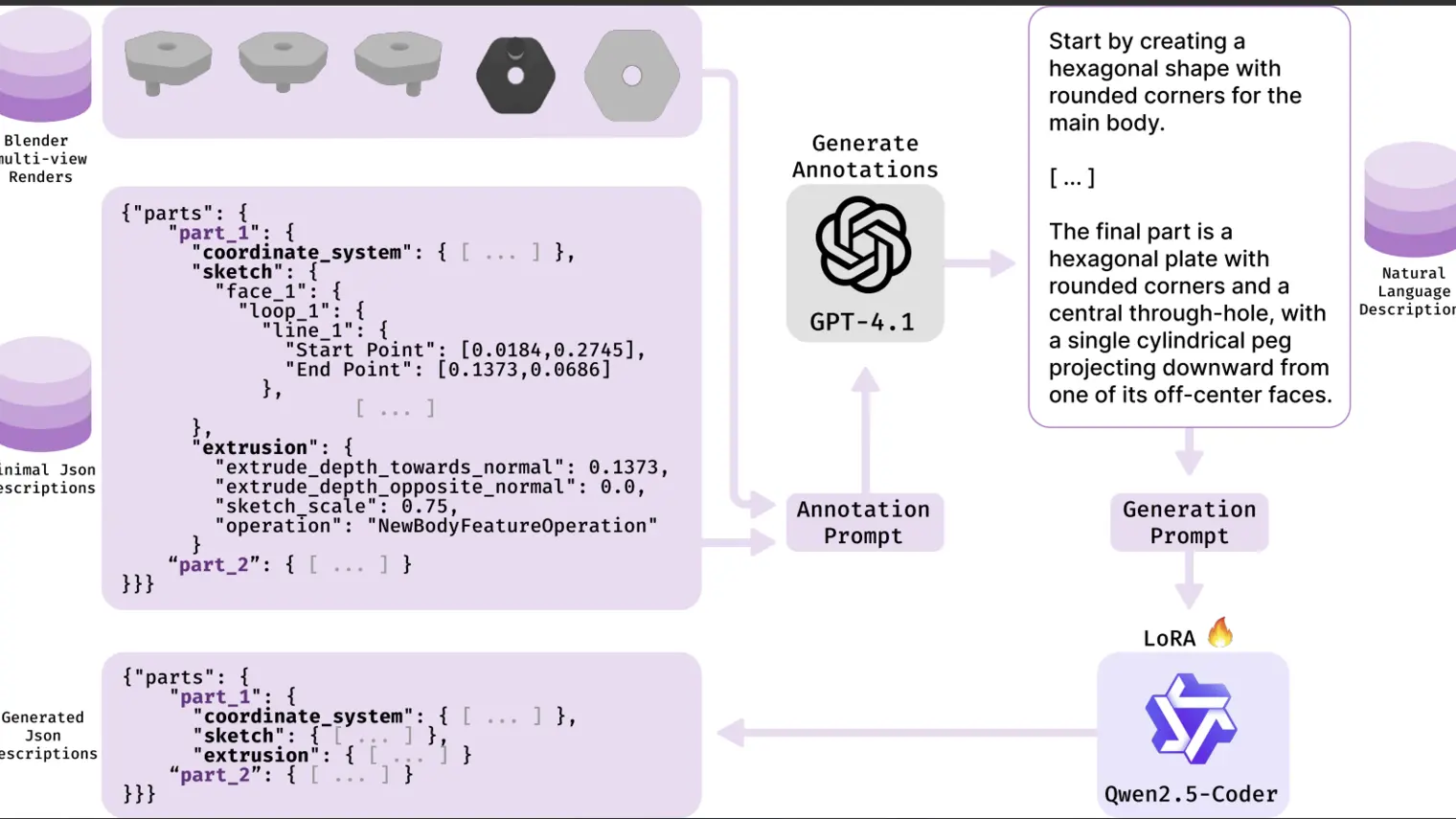
Imaginez un scénario futuriste dans lequel une équipe de chefs robotiques travaillent ensemble pour préparer des omelettes. Bien qu’il soit souhaitable que ces robots utilisent les modèles les plus puissants et fiables possibles, il est également impératif qu'ils suivent le rythme d'un monde en constante évolution. Les ingrédients doivent être ajoutés au bon moment et l'omelette doit être surveillée afin que tout cuise uniformément. Si les robots n'agissent pas assez vite, l'omelette brûlera à coup sûr. Ils doivent également faire face à l'incertitude concernant les actions de leur partenaire et s'adapter en conséquence.
L'apprentissage par renforcement en temps réel
En apprentissage par renforcement (RL), il est généralement supposé que l'agent interagit avec l'environnement dans un jeu au tour par tour idéalisé. On suppose que l'environnement se « met en pause » pendant que l'agent calcule ses actions et apprend de ses expériences. De même, on suppose que l'agent se « met en pause » pendant que l'environnement passe à son état suivant.
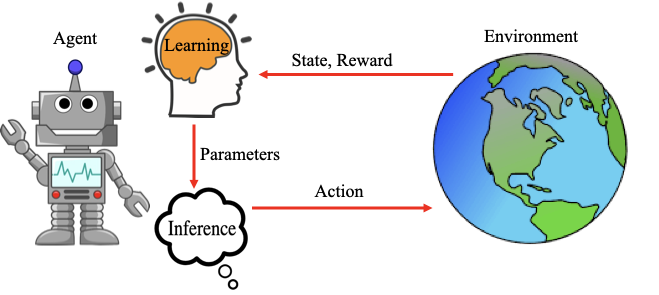
Le diagramme ci-dessous met en évidence deux difficultés majeures dans les environnements en temps réel et qui ne sont pas rencontrées dans les conceptions standard du RL au tour par tour. La première est que l'agent peut ne pas agir à chaque étape de l'environnement en raison de temps d'inférence d'action élevés. Cela conduit à une nouvelle source de sous-optimalité expérimentée par les agents que nous appelons le regret d'inaction. La deuxième difficulté soulignée est que les actions sont calculées à partir d'états obsolètes, ce qui entraîne des actions ayant un impact retardé sur l'environnement. Cela conduit à une autre nouvelle source de sous-optimalité, particulièrement proéminente dans les environnements stochastiques, que nous appelons le regret de délai. Ce billet de blogue résume deux articles complémentaires de notre laboratoire à Mila présentés à ICLR 2025. Le premier présente une solution pour minimiser le regret d'inaction et le second présente une solution pour minimiser le regret de délai.
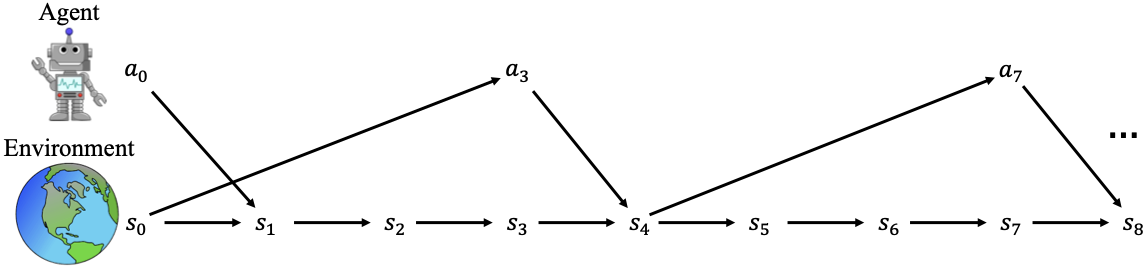
Minimiser l'inaction : inférence échelonnée
Dans le premier article, nous sommes partis du constat que le niveau d'inaction augmente à mesure que le nombre de paramètres du modèle augmente dans le paradigme d'interaction RL standard au tour par tour. La communauté RL doit alors envisager de nouveaux cadres de déploiement pour permettre le RL à l'échelle des modèles de fondation dans le monde réel. À cette fin, nous proposons un cadre pour l'inférence et l'apprentissage asynchrones multi-processus.
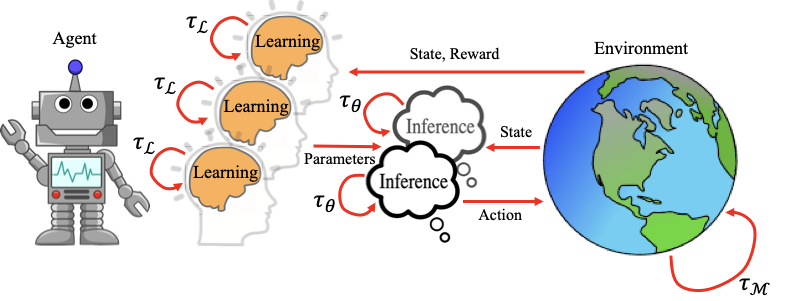
Dans ce cadre, nous permettons à l'agent d'utiliser au maximum sa capacité de calcul disponible pour effectuer des inférences et un apprentissage asynchrones. Plus précisément, nous proposons deux algorithmes dans notre article pour échelonner les processus d'inférence. L'idée de base est que nous voulons décaler de manière adaptative les processus d'inférence parallèles afin qu'ils prennent des actions dans l'environnement à des intervalles réguliers plus rapides. Nous démontrons qu'avec l'un ou l'autre de nos algorithmes, il est possible de déployer un modèle arbitrairement grand avec un temps d'inférence arbitrairement grand de telle sorte qu'il agisse à chaque étape de l'environnement et élimine le regret d'inaction si une puissance de calcul suffisante est disponible.
Expériences en temps réel
Nous avons mis notre nouveau cadre à l'épreuve sur des simulations en temps réel de Game Boy et d'Atari qui sont synchronisées avec leur fréquence d'affichage et les protocoles d'interaction des humains lorsqu'ils jouent à ces jeux sur leurs consoles. Ci-dessous, nous mettons en évidence la performance supérieure de l'inférence et de l'apprentissage asynchrones pour attraper avec succès des Pokémon dans Pokémon Bleu en utilisant un modèle avec 100 millions de paramètres. Notez que l'agent doit non seulement agir rapidement, mais aussi s'adapter constamment à de nouveaux scénarios pour progresser.
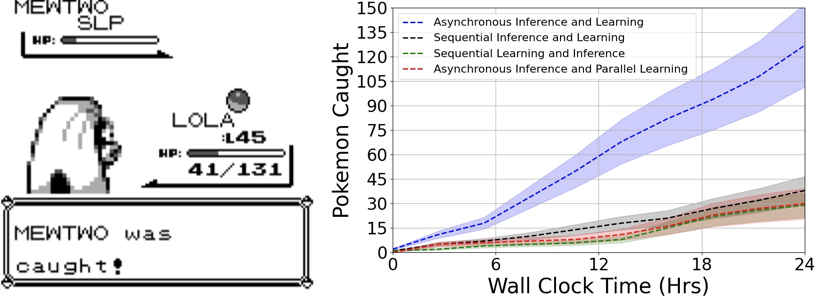
Dans notre article, nous mettons également en évidence la performance de notre cadre dans les jeux en temps réel qui privilégient le temps de réaction comme Tetris. Nous montrons que la performance se dégrade beaucoup plus lentement pour les plus grandes tailles de modèles lorsque l'on utilise l'inférence et l'apprentissage asynchrones. Pourtant, le fait que la performance se dégrade pour les grands modèles est dû au fait que le regret de délai n'est toujours pas résolu.
Minimiser l'inaction et le délai avec un seul réseau neuronal
Notre deuxième article présente une solution architecturale pour minimiser l'inaction et le délai lors du déploiement d'un réseau neuronal dans des environnements en temps réel, où l'inférence échelonnée n'est pas une option. Le calcul séquentiel met en évidence les inefficacités des réseaux profonds, où chaque couche prend approximativement le même temps à s'exécuter. En conséquence, la latence totale augmente proportionnellement à la profondeur du réseau, entraînant des réponses lentes.
Cette limitation est similaire à celle des premières architectures CPU, où les instructions étaient traitées les unes après les autres, ce qui entraînait une sous-utilisation des ressources et un temps d'exécution accru. Les CPU modernes résolvent ce problème avec le pipelining, une technique qui permet d'exécuter différentes étapes de plusieurs instructions en parallèle. Inspirés par ce principe, nous introduisons le calcul parallèle dans les réseaux neuronaux. En calculant toutes les couches à la fois, nous réduisons le regret d'inaction.
Pour réduire davantage le délai, nous introduisons des connexions de saut temporel qui permettent aux nouvelles observations d'atteindre plus rapidement les couches plus profondes, sans avoir à passer par chaque couche précédente.
Notre contribution clé est la combinaison du calcul parallèle et des connexions de saut temporel pour réduire les regrets d'inaction et de délai dans les systèmes en temps réel.
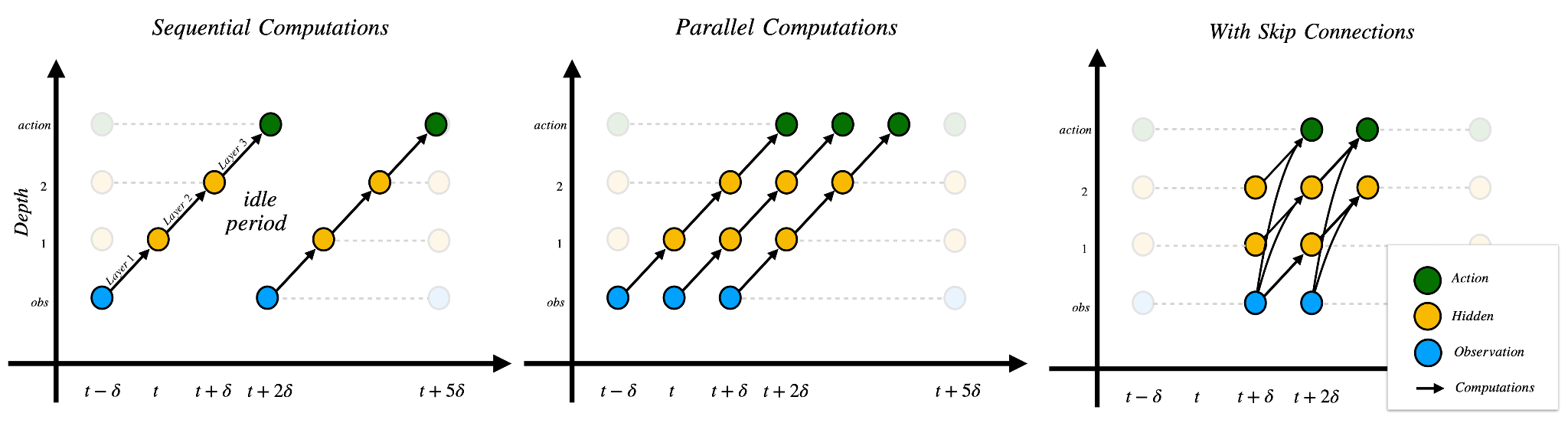
La figure ci-dessous l'illustre. L'axe des ordonnées représente la profondeur de la couche, en commençant par l'observation initiale, suivie des représentations de la première et de la deuxième couche, et se terminant par la sortie d'action, tandis que l'axe des abscisses encode le temps. Une flèche représente donc le calcul d'une couche, qui consomme δ secondes.
Dans la ligne de base (à gauche), une nouvelle observation doit traverser la profondeur N complète séquentiellement, de sorte que l'action devient disponible après Nδ secondes. Le calcul parallèle des couches (au centre) réduit le regret d'inaction en augmentant le débit d'une inférence toutes les Nδ à une inférence toutes les δ. Enfin, les connexions de saut temporel (à droite) réduisent le délai total de Nδ à δ en permettant à la plus récente observation d'atteindre la sortie après un seul δ. Conceptuellement, cela résout le délai en échangeant l'expressivité du réseau avec la nécessité d'incorporer les informations récentes et sensibles au temps dans la plus grande mesure possible.
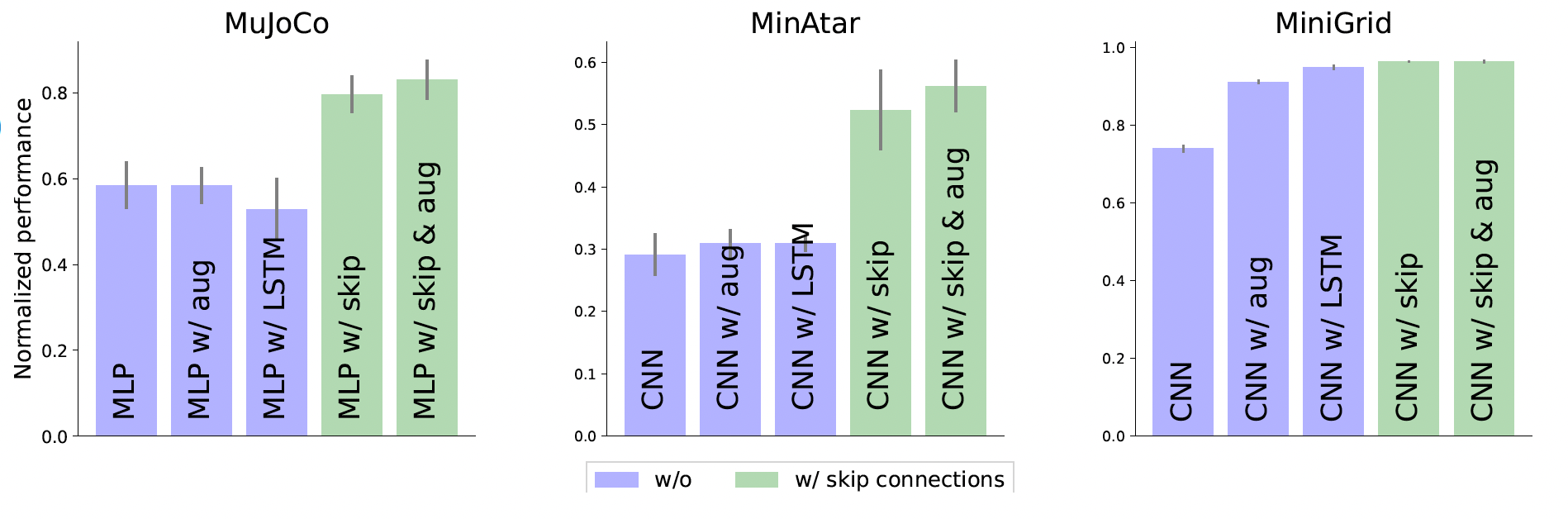
De plus, l'augmentation des entrées avec des actions/états passés restaure la propriété markovienne, améliorant la stabilité de l'apprentissage même en présence de délai. Cela réduit à la fois le délai et le regret lié à l'optimisation, comme le montrent nos résultats. Les colonnes les plus à droite de la figure ci-dessous correspondent à notre meilleure configuration : utilisant le calcul parallèle, les connexions de saut temporel et l'augmentation d'état.
Combiner les deux
L'inférence asynchrone échelonnée et les connexions de saut temporel sont orthogonales, mais complémentaires. Tandis que les connexions de saut temporel réduisent le délai entre l'observation et l'action au sein d'un modèle, l'inférence échelonnée garantit que les actions sont délivrées de manière cohérente même avec des modèles volumineux. Ensemble, elles découplent la taille du modèle de la latence d'interaction, permettant le déploiement d'agents expressifs à faible latence dans des environnements en temps réel. Cela a de fortes implications pour les domaines à enjeux élevés comme la robotique, les véhicules autonomes et les opérations financières, où la réactivité est essentielle. En permettant aux grands modèles d'agir à des fréquences élevées sans compromettre l'expressivité, ces méthodes marquent une étape vers la mise en pratique de l'apprentissage par renforcement pour les applications du monde réel, sensibles à la latence.