* Le contenu de cet article sera présenté sous forme de communication orale à ICLR 2024.
Objet
Nos univers tridimensionnels sont truffés de formes sans épaisseur comme les t-shirts et les drapeaux. En graphisme, ces objets sont généralement modélisés sous forme de « maillages non étanches », des surfaces délimitées d’une infinie minceur qui sont discrétisées au moyen de polygones. Ce sont ces maillages qui permettent d’obtenir un rendu réaliste simulant les lois de la physique. Aussi importantes soient-elles, la création et la génération de maillages non étanches de bonne qualité constituent un processus long et fastidieux pour les artistes et les concepteurs graphiques. Peut-on par conséquent trouver une méthode de représentation qui facilite la reconstruction et la génération de maillages non étanches?
Dans cet article, nous proposons une approche de représentation générique qui permet de paramétrer des maillages quelconques et qui débouche sur : 1) un procédé de reconstruction efficace des maillages non étanches à partir d’images multivues; 2) le premier modèle de diffusion permettant de générer des maillages non étanches de haute qualité.
Représentation
Paramétrage des maillages étanches
Commençons par voir une méthode bien connue de paramétrage des maillages étanches, ces maillages de surfaces d’un volume dont on peut distinguer l’intérieur et l’extérieur. Imaginons que nous avons une forme continue. Pour chaque point dans l’espace, nous pouvons mesurer la fonction de distance signée, dans laquelle la magnitude indique la distance par rapport à la surface et le signe indique sa position (à l’intérieur ou à l’extérieur du volume). Si l’on mesure la fonction de distance signée de chaque point dans l’espace, on obtient un champ scalaire continu appelé « champ de distance signé » (CDS).

Sans surprise, c’est à la surface de l’objet que les valeurs du CDS égalent zéro. La manière la plus simple d’extraire un maillage consiste à discrétiser l’espace à l’aide d’une grille, en supposant que les valeurs du CDS peuvent être interpolées linéairement dans chacune de ses cellules. Ainsi, tous les niveaux zéro correspondent à des polygones planaires pouvant être déterminés à l’aide d’une méthode simple : le fractionnement en deux parties. Si l’on utilise une grille tétraédrique, cet algorithme porte alors le nom de « Marching Tetrahedra ». Comme la formule d’interpolation est une fonction continue qui est presque toujours dérivable, elle constitue une représentation valable des maillages étanches.
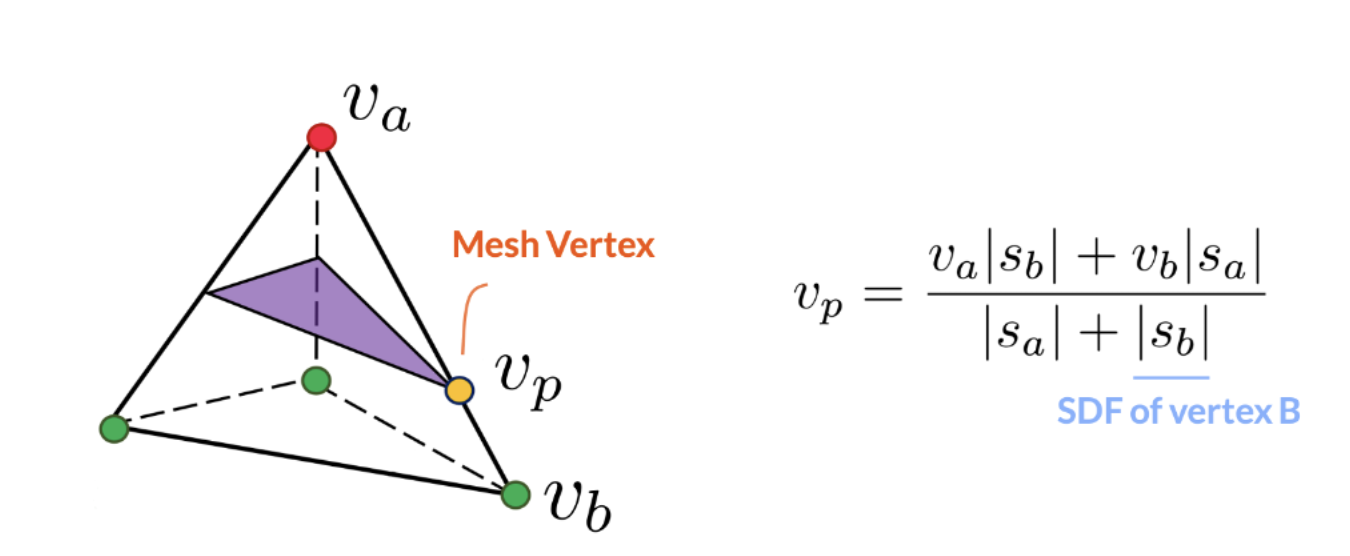
Des maillages étanches aux maillages non étanches
En l’absence de distinction entre l’intérieur et l’extérieur, les maillages non étanches ne comportent que des « champs de distance non signés » (CDNS), c’est-à-dire des CDS dépourvus de signes. Comme les CDNS sont invariablement non négatifs, la méthode de fractionnement en deux parties ne s’applique plus. Il existe bien entendu des solutions de rechange, mais aucune n’aboutit à une reconstruction satisfaisante fondée sur les lois de la physique. Aucune ne permet non plus de générer les maillages non étanches d’une grande fidélité dont dépend la représentation d’objets comme les vêtements. Existe-t-il alors un moyen d’appliquer la méthode de fractionnement en deux parties aux maillages non étanches?
Pour répondre à cette question, observons un phénomène très simple, à savoir le principe selon lequel tout disque peut être déformé pour épouser une sphère, un peu comme les continents qui recouvrent la planète Terre. Imaginons maintenant que nous voulons extraire la forme de « fantôme » d’un modèle sphérique 2D à maillage étanche. Nous pouvons définir un CDS sur une sphère (« CDSs »), soit essentiellement le champ de distance signé mesuré à partir de la courbe la plus courte de la sphère jusqu’au contour de la forme non étanche. Une fois que nous avons trouvé l’isoligne où les valeurs du CDSs égalent zéro, nous pouvons retrancher la région bleue de l’illustration et obtenir (différentiellement) le maillage non étanche. Cette règle d’extraction s’apparente au fonctionnement du « Marching Tetrahedra » dans un espace tridimensionnel.
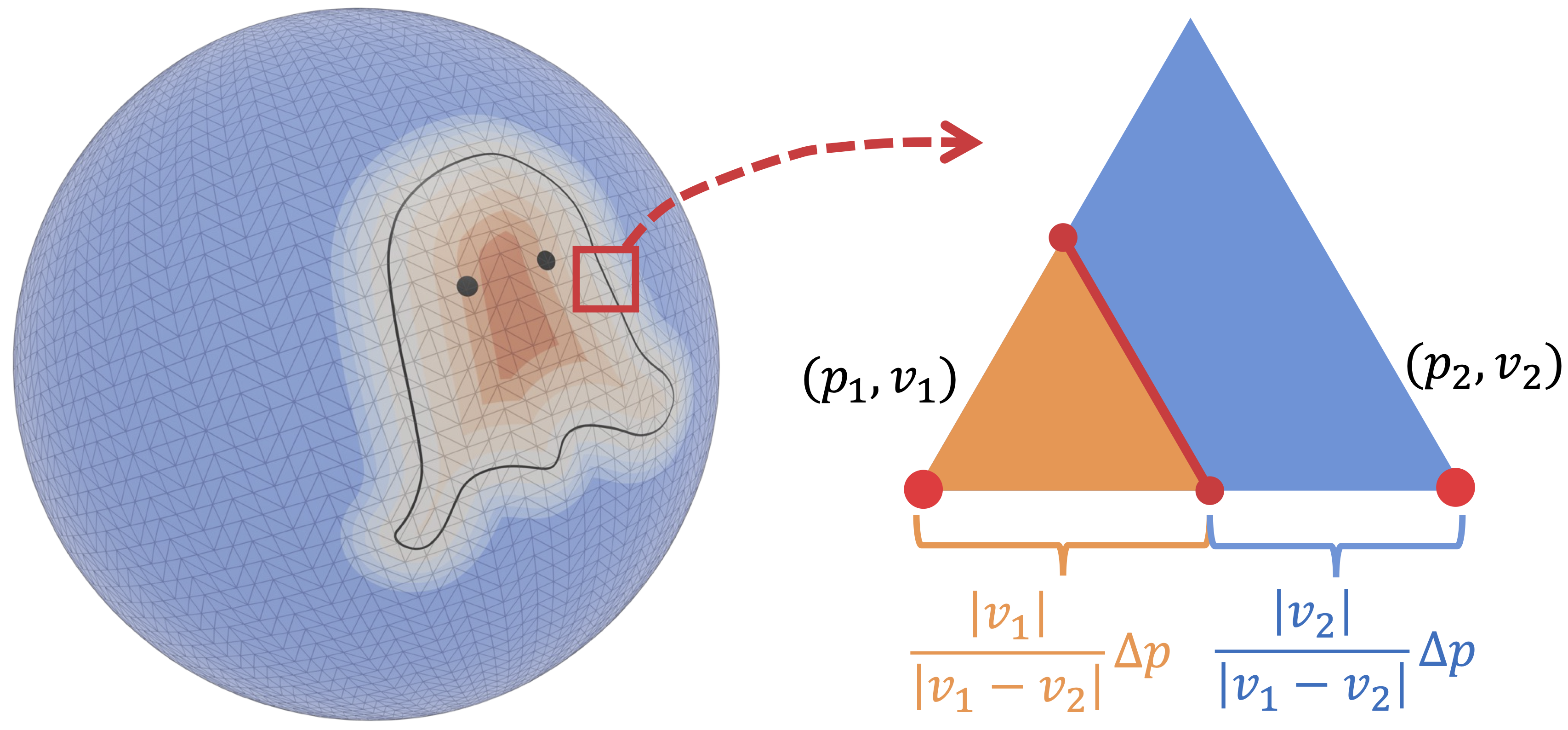
Cet exemple simple peut être étendu aux cas qui exigent d’extraire la surface non étanche de modèles étanches généraux et assimilables, représentés par des grilles tétraédriques de valeurs de CDS (ce que nous avons montré dans la section précédente). Dans un tel cas, nous pouvons définir des « CDSs généralisés » à partir de la grille tétraédrique (où sont enregistrées les valeurs de CDS), qui sont ensuite projetés sur le modèle étanche assimilé. Cette règle d’extraction peut être appliquée en répertoriant tous les cas de figure qui comportent des signes CDS et CDSs différents. Nous appellerons notre représentation « G-Shell », abréviation de « Ghost on the Shell », d’après la série de mangas Ghost in the Shell.
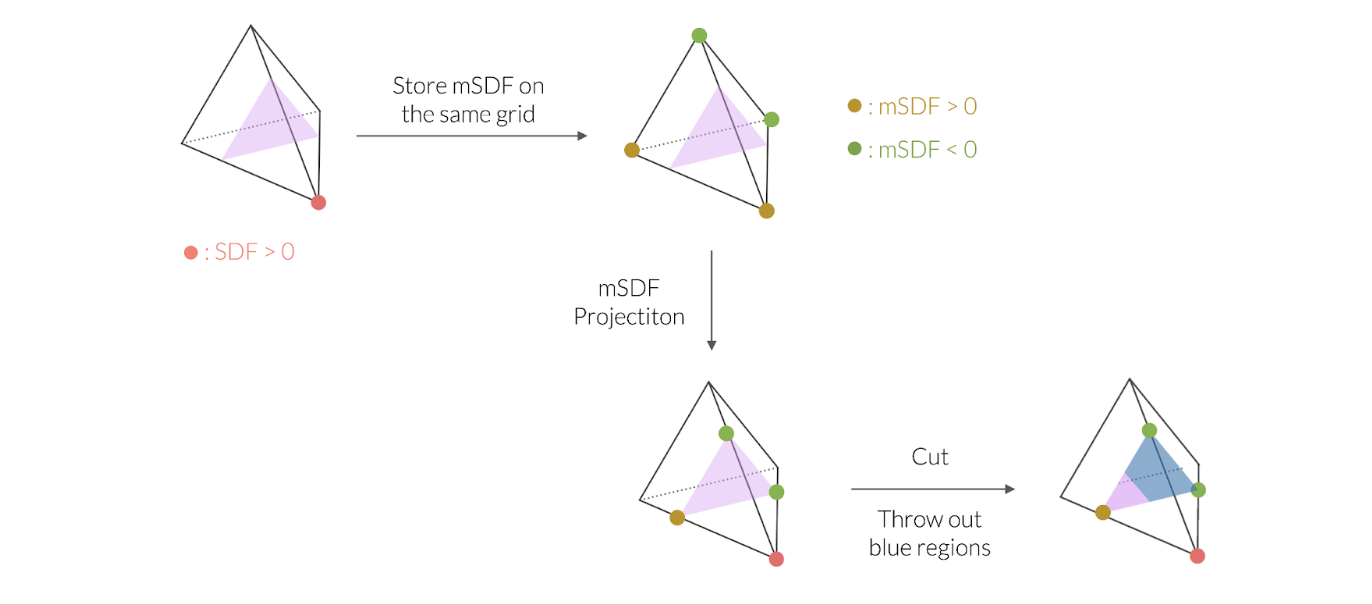
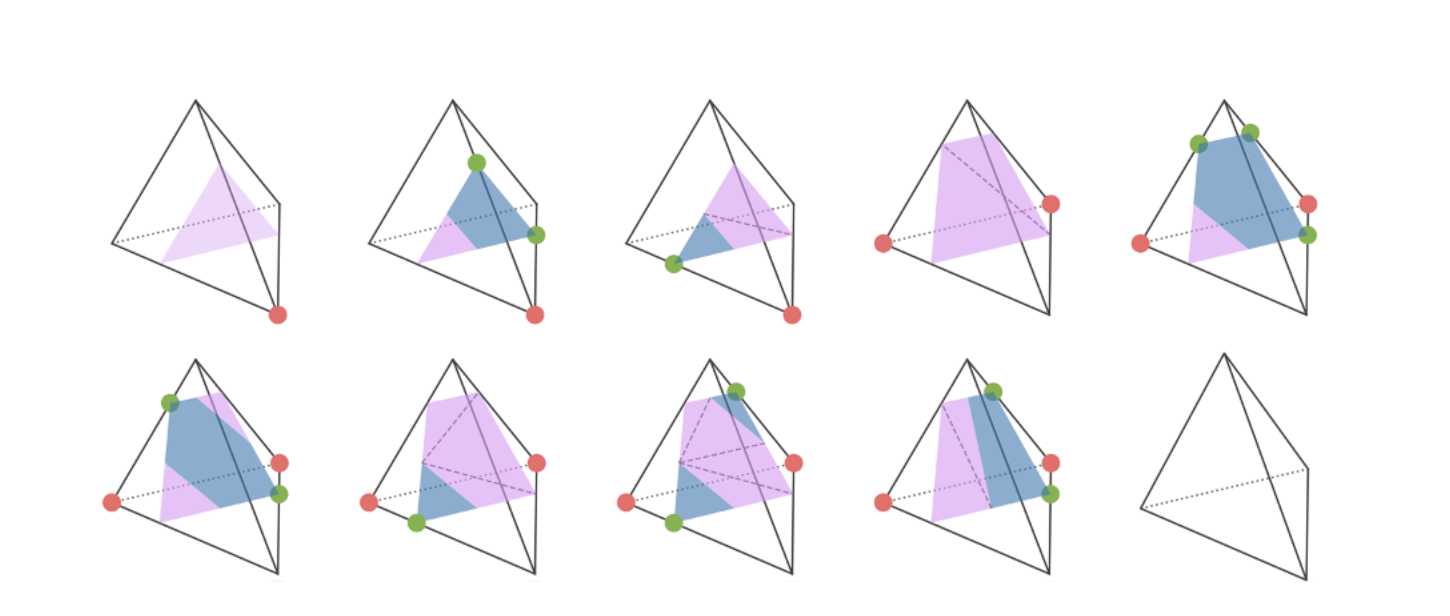
Vers une meilleure topologie de maillage
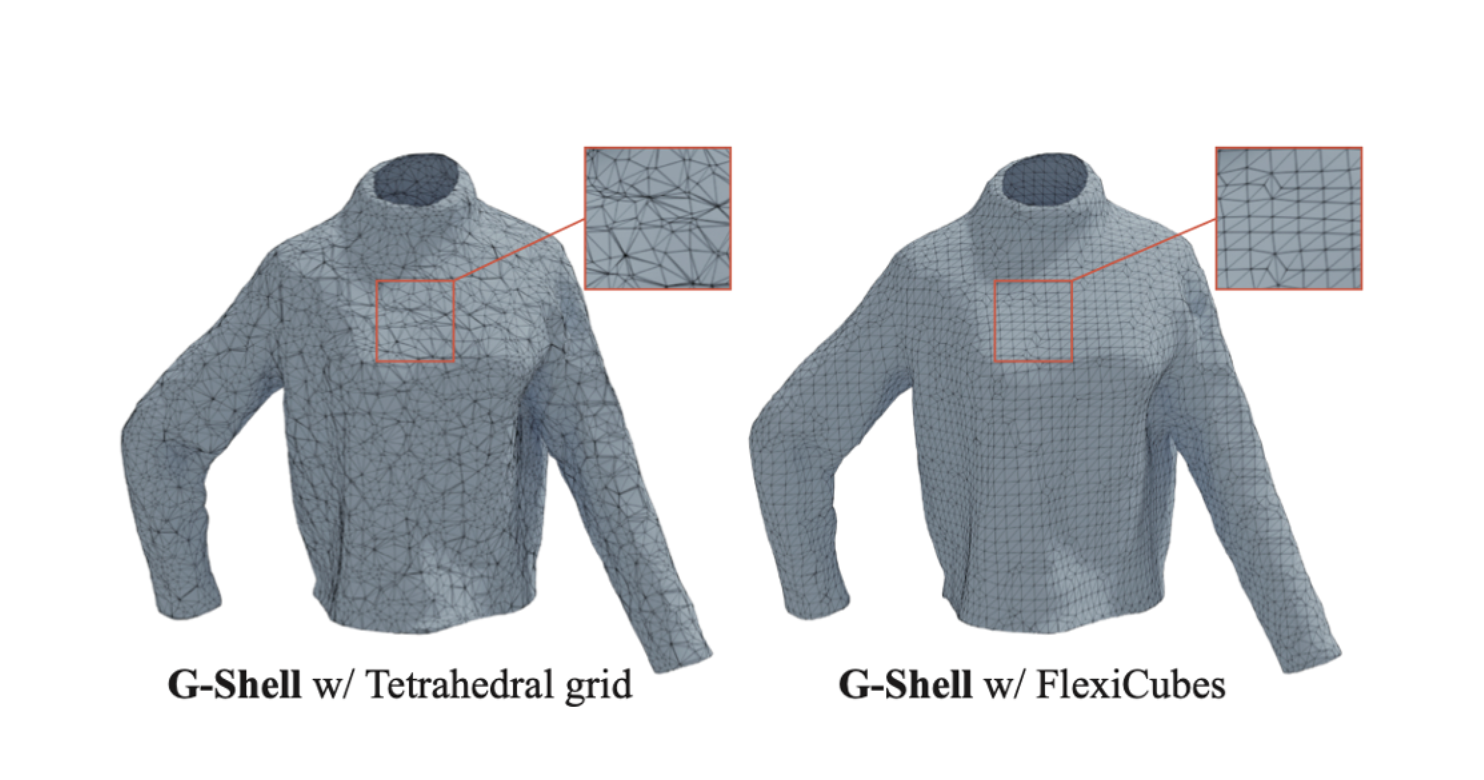
Au lieu d’appliquer naïvement les grilles tétraédriques, nous pouvons obtenir une topologie de maillage nettement supérieure en combinant la représentation G-Shell et une méthode d’extraction récente appelée « FlexiCubes » qui permet d’obtenir des maillages avec triangles de taille régulière.
Reconstruction
Avec la représentation G-Shell, il est presque facile de reconstruire les images à l’aide d’un moteur de rendu de maillage dérivable. Il suffit alors d’une simple supervision des images pour optimiser le maillage. Il y a toutefois deux ombres au tableau.
Moteur de rendu sensible à l’occlusion
L’occlusion est le phénomène qui fait en sorte que la face interne des formes (p. ex., une robe longue) est assombrie. Les moteurs de rendu doivent en tenir compte pour pouvoir restituer la topologie des formes. C’est pourquoi nous utilisons une méthode de reconstruction appelée « Nvdiffrec ». Selon cette méthode, le moteur de rendu reproduit le tracé des rayons lumineux et détermine s’ils sont occultés ou non afin de représenter fidèlement les jeux d’ombre et de lumière.
Régularisation
Il arrive qu’un trou n’apparaisse pas sur les masques de segmentation binaires. Si la forme complète est définie de telle manière que le trou est comblé, aucun signal existe permettant de superviser le processus d’optimisation puisque seuls les contours dans l’image présentent un dégradé de valeurs de CDSs. Pour corriger ce problème, nous introduisons une technique de régularisation de la fonction de perte afin que les valeurs de CDSs passent en zone négative (rappelons que les parties éliminées ont des valeurs de CDSs négatives). Cependant, nous ne voulons pas que cet ajustement influence les autres signaux de supervision. C’est pourquoi nous intégrons également une force contraire pour éviter que les valeurs de CDSs en bordure du maillage ne diminuent.
Résultats empiriques
Notre méthode, qui combine le moteur de rendu Nvdiffrec et notre représentation G-Shell, permet de reconstruire fidèlement des formes non étanches (en obtenant seulement les trous voulus) à partir d’images multivues (rendues avec des effets d’éclairage réalistes) et de masques binaires. En comparaison, les méthodes de référence génèrent des surfaces bruitées ou omettent certains trous (l’extrémité des manches, par exemple). C’est la première fois qu’on arrive à reconstruire une géométrie non étanche en même temps que les effets d’éclairage et la surface des matériaux.

Génération
Comme nous enregistrons les valeurs de CDS et CDSs dans une grille tétraédrique ordinaire (déformable) de taille fixe, nous parvenons à créer le premier modèle de diffusion générant des maillages non étanches. Vous trouverez ci-dessous quelques exemples d’images de vêtements réalisées au moyen d’un modèle de diffusion entraîné à partir de Cloth3D, un ensemble de données de maillages non étanches pour le rendu des vêtements.

Remarques
Grâce à G-Shell, nous avons : 1) mis au point une méthode de reconstruction efficace qui permet de reproduire simultanément et fidèlement la géométrie, les matériaux et les effets d’éclairage des maillages non étanches à partir d’images multivues réalistes; et 2) créé le premier modèle de diffusion permettant de générer des maillages non étanches. Pour autant, notre méthode ne permet pas de résoudre des cas tels que les intersections de l’objet par lui-même (p. ex., des poches sur un t-shirt) et peut s’avérer passablement gourmande en mémoire. Il reste encore du travail à faire afin d’explorer différentes opérations en aval et de tirer le meilleur parti des possibilités qu’offre cette nouvelle méthode de représentation.
Références
1. Ghost on the Shell: An Expressive Representation of General 3D Shapes. Zhen Liu, Yao Feng, Yuliang Xiu, Weiyang Liu, Liam Paull, Michael J. Black, Bernhard Schölkopf. ICLR 2024.
2. MeshDiffusion: Score-based Generative 3D Mesh Modeling. Zhen Liu, Yao Feng, Michael J. Black, Derek Nowrouzezahrai, Liam Paull, Weiyang Liu. ICLR 2023.
3. « Shape, Light, and Material Decomposition from Images using Monte Carlo Rendering and Denoising ». Jon Hasselgren, Nikolai Hofmann, Jacob Munkberg. NeurIPS 2022.
4. « Flexible Isosurface Extraction for Gradient-Based Mesh Optimization ». Tianchang Shen, Jacob Munkberg, Jon Hasselgren, Kangxue Yin, Zian Wang, Wenzheng Chen, Zan Gojcic, Sanja Fidler, Nicholas Sharp, Jun Gao. ACM Trans. on Graph. (SIGGRAPH 2023).
Site Web :https://gshell3d.github.io/
Répertoire GitHub :https://github.com/lzzcd001/GShell/