*This paper was accepted as an oral presentation at ICLR 2024.
Motivation
Our 3D worlds are full of thin shapes like T-shirts and flags. These shapes are typically modeled in the modern graphics industry for realistic rendering and physical simulation as so-called “non-watertight meshes” – infinitely-thin and borderer surfaces discretized with polygons. Creating and generating high-quality non-watertight meshes, though highly important, is typically a lengthy and cumbersome process for artists and designers. Can we figure out a representation that facilitates reconstruction and generation of non-watertight meshes?
In this work, we propose a generic representation that parameterizes generic meshes and successfully enable 1) an efficient and effective reconstruction method for non-watertight meshes from multi-view images and 2) the first diffusion model that can generate high-quality non-watertight meshes.
Representation
Watertight Mesh Parameterization
Let’s start with the rather well-understood way for parameterizing watertight meshes – the meshes for surfaces of a volume from which you can tell the inside from the outside. Suppose you have a continuous shape. For any point in space, you can measure its signed distance, in which the magnitude indicates the distance to the surface and the sign indicates its location (inside or outside the volume). If we measure the signed distance at every point in space we get a continuous scalar field, called a signed distance field (SDF).

Not surprisingly, the surface of the object is where SDF values equal zero. The easiest way to extract a mesh is basically to discretize the whole space with a grid, and in each tiny cell of the grid we assume SDF values can be linearly interpolated. As a result, the zero levelsets are all planar polygons which can be found by the simple bisection method. The algorithm is called Marching Tetrahedra if we use a tetrahedral grid. As the interpolation formula is continuous and differentiable almost everywhere, it is a valid representation of watertight meshes.
From Watertight to Non-Watertight
For non-watertight meshes, there is no distinction between inside and outside, and therefore we only have “unsigned distance fields” (UDF), basically SDF without signs. As a UDF is always non-negative, the convenient bisection method is no longer available. While some alternatives exist, none of them allow robust and efficient physics-based reconstruction and high-fidelity generation of non-watertight meshes, which are essential for objects like garments. Can we figure out a way to re-enable the bisection method for non-watertight meshes?
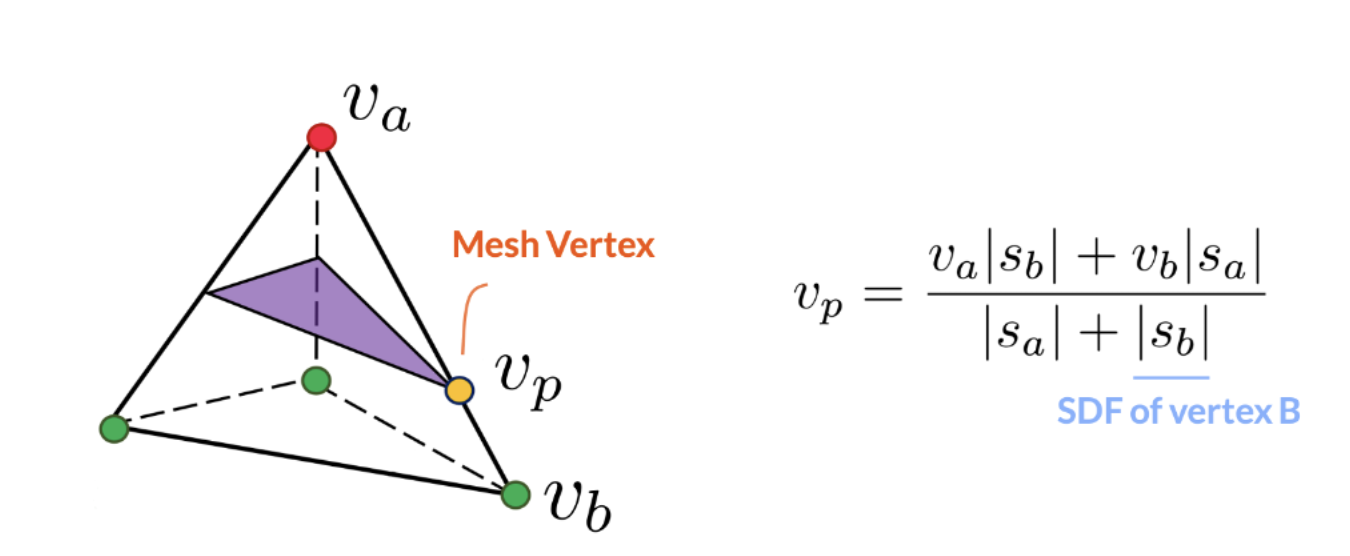
We take inspiration from the following simple observation: any disk-like shape can be deformed so that it eventually fits perfectly on a sphere, just like continents floating on the Earth. Now suppose our objective is to extract the “ghost” from a 2D watertight sphere template. We can define a “manifold SDF” (mSDF) – basically the field of signed distance measured by the shortest curve on the sphere to the non-watertight shape boundary. Once we figure out the zero isoline where mSDF values equal zero, we can discard the blue region in the illustration and (differentiably) obtain the non-watertight mesh. The extraction rule is similar to how Marching Tetrahedra works in the 3D space.
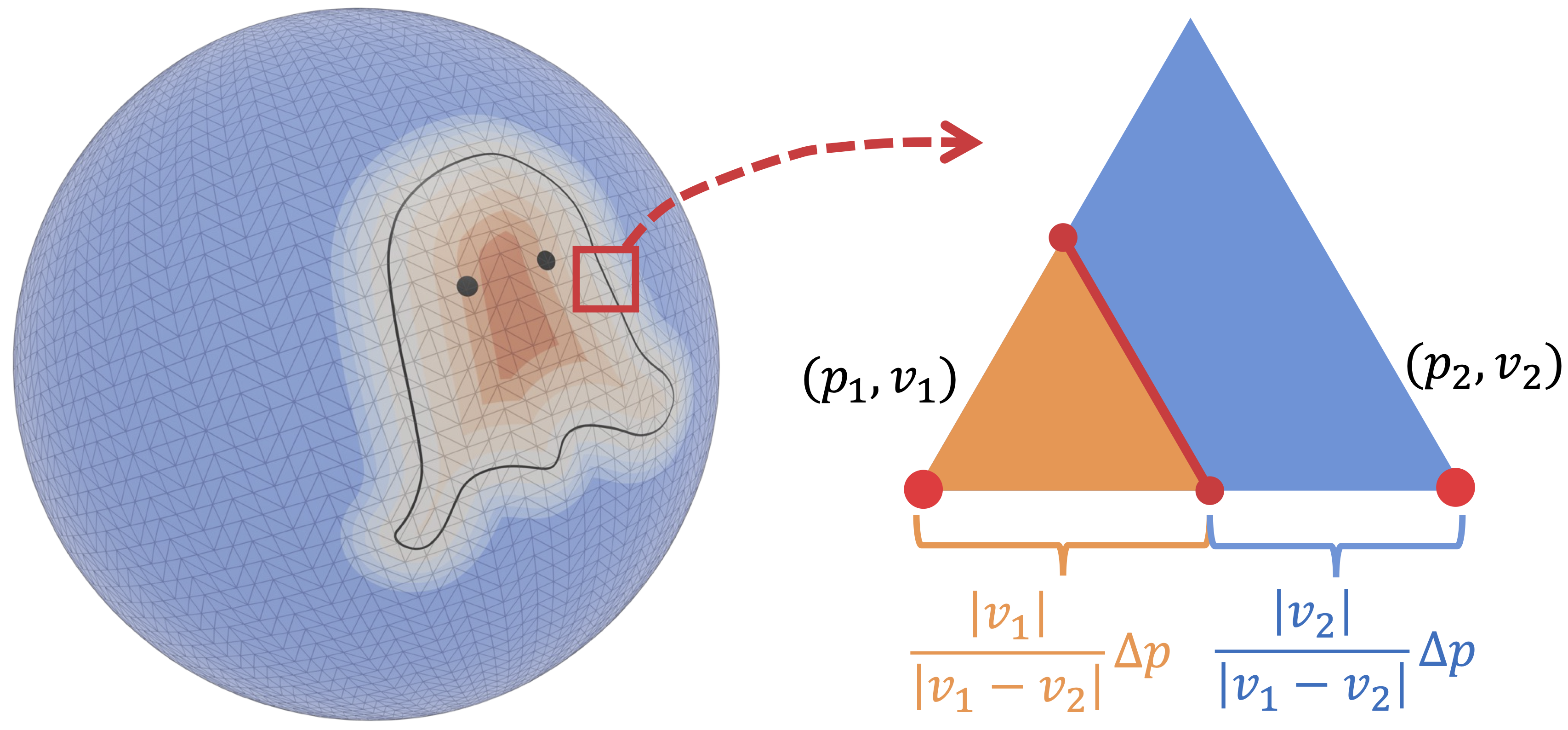
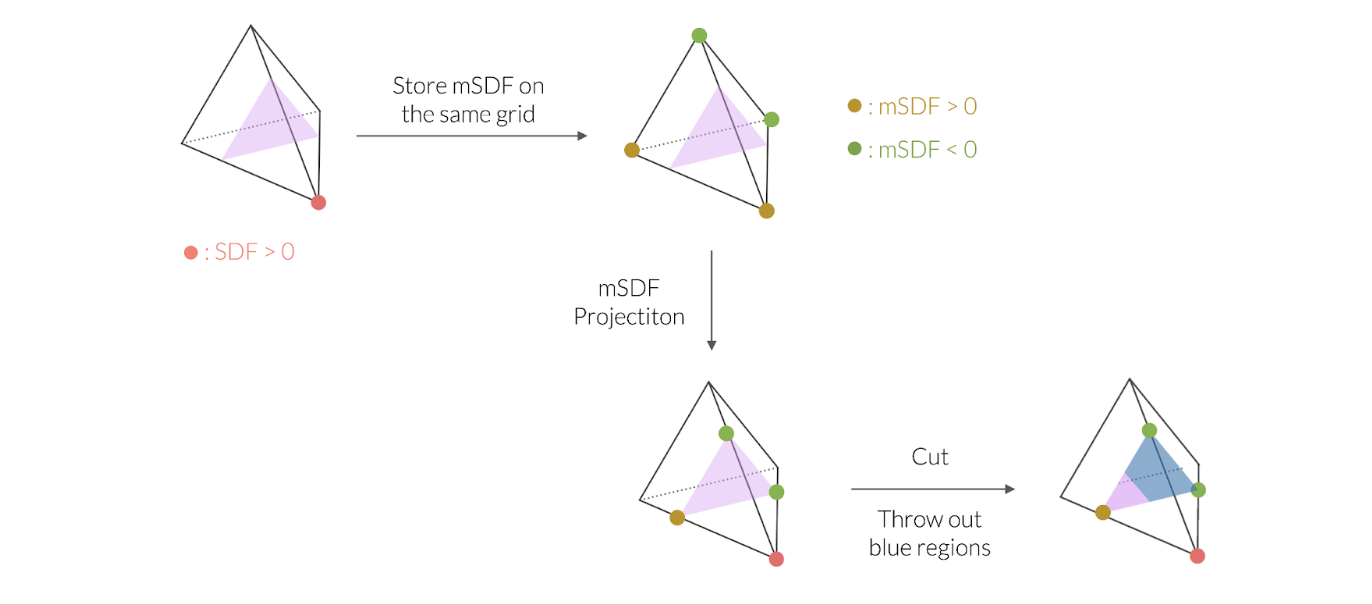
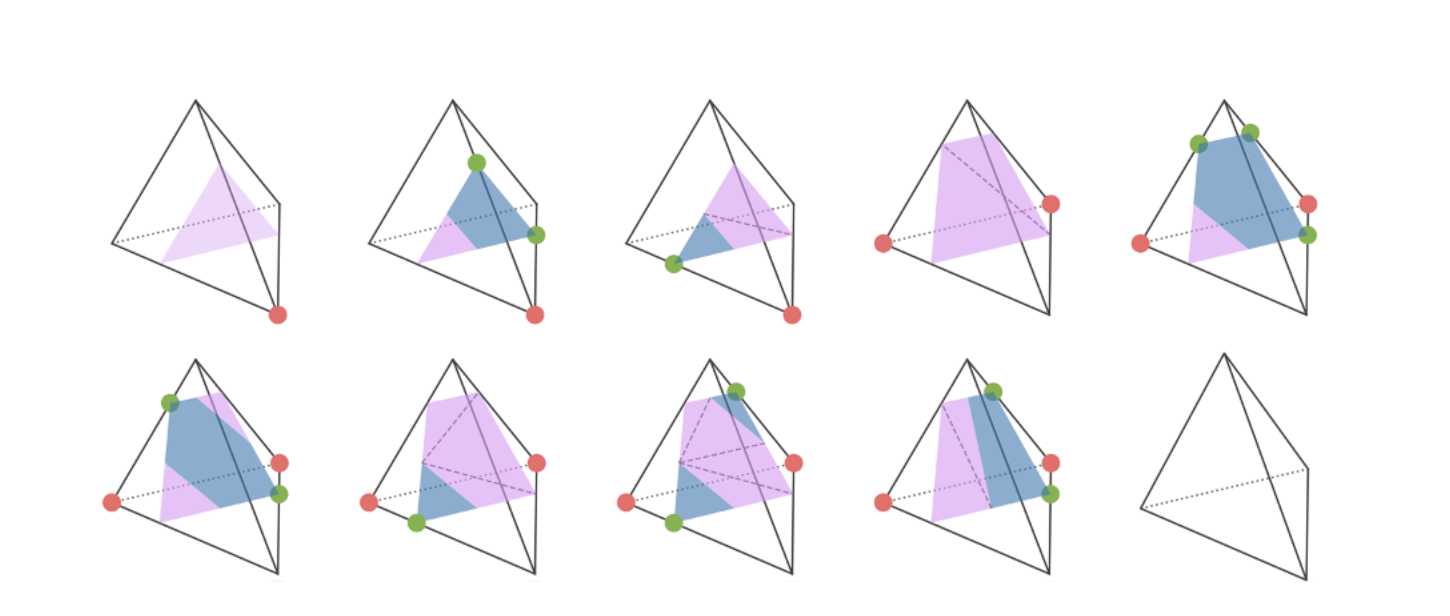
We may generalize this simple case to ones where the non-watertight surface should be extracted from general and learnable watertight templates represented by tetrahedral grids of SDF values (which is shown in the previous section). In such a case, we can define some “generalized mSDF” on the tetrahedral grid (where we store SDF values) which are later projected to the learned watertight template. The mesh extraction rule can be implemented by enumerating all cases with different SDF and mSDF signs. We call our representation G-Shell (short for “Ghost on the Shell”, inspired by the manga series “Ghost in the Shell”).
Better Mesh Topology
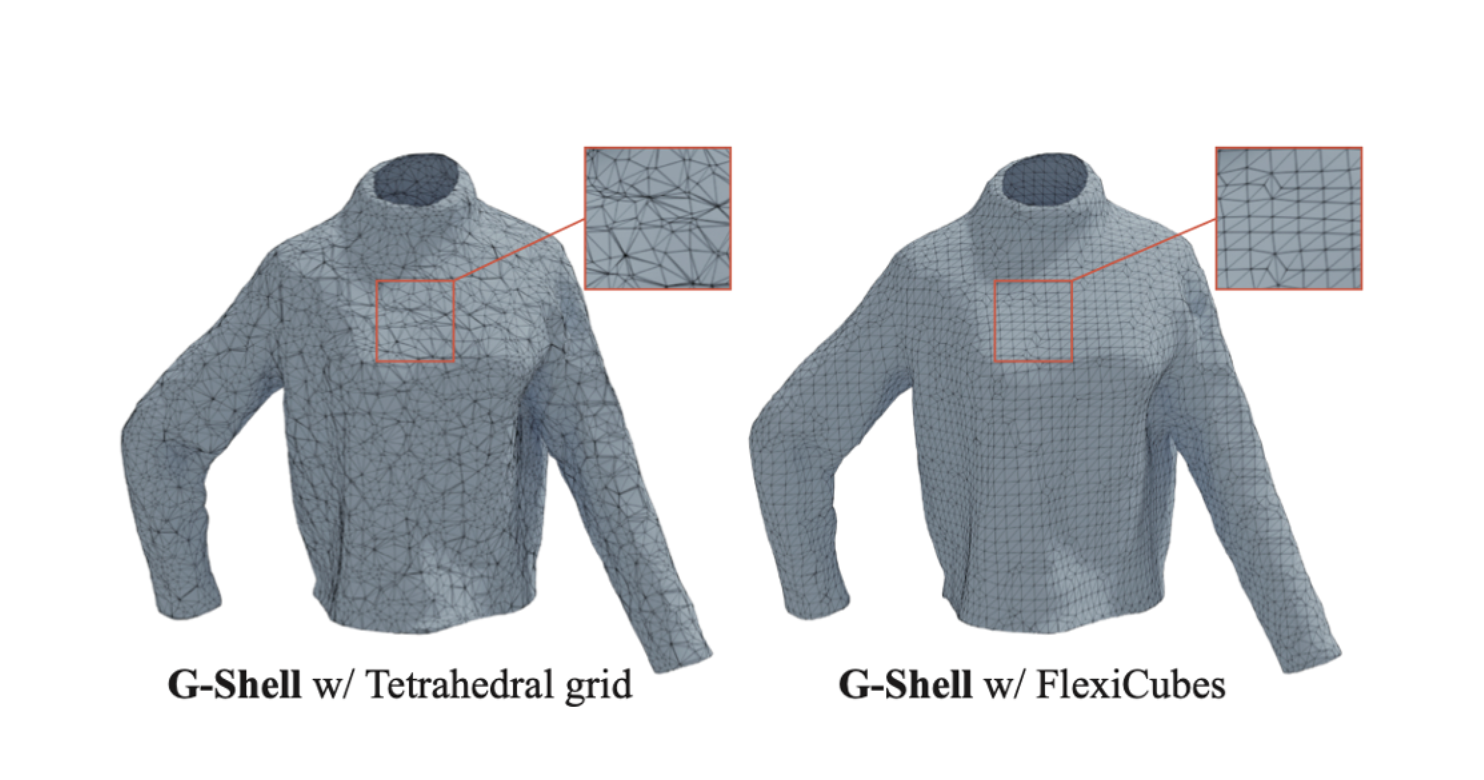
Instead of the naïve implementation with tetrahedral grids, we can combine G-Shell with a recent mesh extraction method called FlexiCubes for much better mesh topology (i.e., with regularly sized triangles).
Reconstruction
With the G-Shell representation, it is almost straightforward to use a differentiable mesh renderer to render images, so that we can optimize the mesh with image supervision. However, there are two subtle issues to solve.
Occlusion-aware renderer
The inner side of shapes like a long dress is typically less illuminated due to occlusion. A mesh renderer must take this fact into account so that shape topology can be recovered. For this reason, we leverage a reconstruction method called Nvdiffrecmc in which the renderer traces light rays and determines if they are occluded or not for illumination.
Regularization
There are cases when a hole cannot be seen in binary segmentation masks. If we initialize the whole shape in the way that the hole is closed, there is no supervision signal for the optimization process, as only the edges in the rendered images receive gradients for mSDF values. To overcome this issue, we introduce a regularization loss so that mSDF values are encouraged to be negative (recall that discarded regions have negative mSDF values). However, we do not want this term to dominate other signals – as a result, we also introduce a counter force to prevent the mSDF values on the mesh boundary from decreasing.
Empirical Results
Our method (which combines the Nvdiffrecmc renderer with our G-Shell representation) is able to reconstruct non-watertight shapes accurately (with all and only necessary holes created) given multiview images (rendered with realistic lighting) and binary masks. In contrast, baseline methods either create noisy surfaces or fail to create necessary holes (e.g. for the end of sleeves). Moreover, it is the first time that non-watertight geometry can be reconstructed jointly with lighting and surface material.

Generation
Since we store SDF and mSDF in a fixed-sized regular (deformable) tetrahedral grid, we are able to build the first diffusion model that generates non-watertight meshes. Below we show the generated garment examples, with a diffusion model trained on Cloth3D, a non-watertight garment mesh dataset.

Remarks
With our G-Shell representation, we 1) develop an efficient reconstruction method that can jointly and accurately reconstruct geometry, material and lighting for non-watertight meshes from realistic multiview images, and 2) build the first diffusion model to generate non-watertight meshes. Still, our method is not able to handle cases like self-intersections (e.g., pockets on T-shirts) and can suffer from relatively high memory consumption. It remains for future work to explore different downstream tasks for fully leveraging the capability of this new representation.
References
1. Ghost on the Shell: An Expressive Representation of General 3D Shapes. Zhen Liu, Yao Feng, Yuliang Xiu, Weiyang Liu, Liam Paull, Michael J. Black, Bernhard Schölkopf. ICLR 2024.
2. MeshDiffusion: Score-based Generative 3D Mesh Modeling. Zhen Liu, Yao Feng, Michael J. Black, Derek Nowrouzezahrai, Liam Paull, Weiyang Liu. ICLR 2023.
3. Shape, Light, and Material Decomposition from Images using Monte Carlo Rendering and Denoising. Jon Hasselgren, Nikolai Hofmann, Jacob Munkberg. NeurIPS 2022.
4. Flexible Isosurface Extraction for Gradient-Based Mesh Optimization. Tianchang Shen, Jacob Munkberg, Jon Hasselgren, Kangxue Yin, Zian Wang, Wenzheng Chen, Zan Gojcic, Sanja Fidler, Nicholas Sharp, Jun Gao. ACM Trans. on Graph. (SIGGRAPH 2023)
Website: https://gshell3d.github.io/
GitHub :https://github.com/lzzcd001/GShell/