Comment rendre un modèle de fondation équivariant?

Note de la rédaction : Cet article a été présenté à NeurIPS 2023.

L’apprentissage profond a connu une croissance fulgurante au cours de la dernière décennie. Néanmoins, alors que nous cherchons à raffiner la compréhension et à améliorer les performances des modèles, un défi se dessine clairement : comment s’assurer que nos modèles comprennent les transformations de données? C’est ici qu’intervient l’équivariance, une notion qui peut aider nos réseaux à conserver un comportement cohérent avec les transformations de données. Mais avec l’essor des grands modèles préentraînés, comment pouvons-nous les rendre équivariants sans modifier leur architecture ou réentraîner le modèle à partir de zéro avec l’augmentation des données?

En quoi consiste l’équivariance?

Avant de poursuivre, clarifions un peu le concept. Les réseaux équivariants [1,2,3] sont des réseaux de neurones profonds qui conservent un comportement cohérent lorsque les données d’entrée subissent des transformations, comme la rotation, la mise à l’échelle ou la translation. En termes plus simples, si nous faisons pivoter l’image d’un chat, un réseau équivariant la reconnaîtra toujours comme représentant un chat!

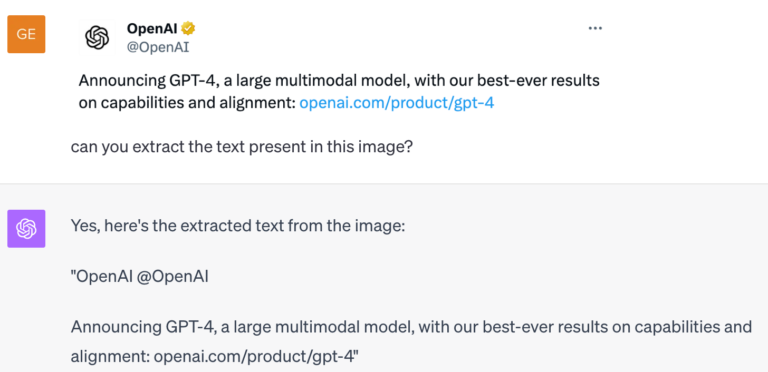
L’avantage, c’est que ces réseaux fournissent des prédictions plus précises et plus robustes, et que leur entraînement nécessite moins d’échantillons. Une excellente chose du point de vue théorique, mais difficile à mettre en œuvre dans la pratique, en particulier pour les grands modèles préentraînés dont les contreparties équivariantes ne sont pas faciles à concevoir ou sont très coûteuses à réentraîner à partir de zéro. Appelés « modèles de fondation », ces modèles massifs préentraînés sur des données issues d’Internet sont extrêmement efficaces pour résoudre et raisonner dans le cadre de différentes tâches. Malgré ces capacités, les modèles de fondation [4] ne sont pas équivariants par nature et ne gèrent généralement pas bien les transformations (voir l’exemple GPT-4 ci-dessous). Notre objectif consiste à intégrer les avantages de l’équivariance dans les modèles de fondation actuels.

La canonisation : découpler l’équivariance de l’architecture

Une solution de rechange récente à la conception de réseaux équivariants a été proposée par Kaba et coll. [5]. Au lieu de modifier l’architecture du réseau pour intégrer l’équivariance, on propose d’apprendre d’abord à transformer les données d’entrée dans un format « standard », également connu sous le nom de « forme canonique ». Ainsi, notre réseau de prédiction de tâche peut travailler sur ce format standardisé, ce qui assure la cohérence. Ce processus implique l’ajout d’un réseau supplémentaire peu coûteux appelé réseau de canonisation, qui apprend à standardiser les données d’entrée. Le réseau primaire qui apprend à résoudre la tâche en fonction des données d’entrée standardisées est appelé réseau de prédiction. Dans cette formulation particulière, pour obtenir l’équivariance, il suffit de s’assurer que le processus de canonisation est invariant par rapport à la transformation des données d’entrée. Cela signifie que, quelle que soit l’orientation des données d’entrée, le processus de canonisation doit toujours les ramener à la même orientation canonique. Ceci est réalisé au moyen d’une architecture équivariante légère et peu coûteuse pour le réseau de canonisation (voir [5] pour plus de détails).

La valeur de cette approche tient à la façon dont le réseau de canonisation sépare l’exigence d’équivariance de l’architecture centrale du réseau de prédiction. Cela signifie que vous pouvez employer n’importe quel réseau de neurones puissant et préentraîné pour réaliser la tâche principale de prédiction.

Cela semble simple? Eh bien, il y a un hic.

Le principal défi consiste à s’assurer que le réseau de canonisation « joue le jeu » avec le réseau de prédiction. Par exemple, le réseau de canonisation peut produire des orientations qui nuisent à l’entraînement du réseau de prédiction, ce qui génère de mauvaises performances. Cela devient important lorsque le réseau de prédiction est préentraîné sur un ensemble de données déterminé. Par exemple, si le réseau de canonisation met toutes les images à l’envers, mais que le réseau de prédiction n’a pas été entraîné sur des images à l’envers, tout le système s’écroule. Il est donc essentiel que le réseau de canonisation produise des orientations de données qui se retrouvent dans la distribution pour le réseau de prédiction préentraîné.

Apprendre à prédire la bonne orientation pour le réseau préentraîné

La magie réside dans la conception de notre fonction de canonisation. Celle-ci ne se contente pas de transformer les données, mais elle le fait en tenant compte de la manière dont notre modèle de prédiction a été initialement entraîné. La clé est de s’assurer que les données transformées (ou standardisées) sont alignées sur les attentes du modèle de prédiction préentraîné. Sur le plan mathématique, nous voulons ramener les orientations prédites hors distribution dans la distribution des orientations que le réseau de prédiction préentraîné a observées.

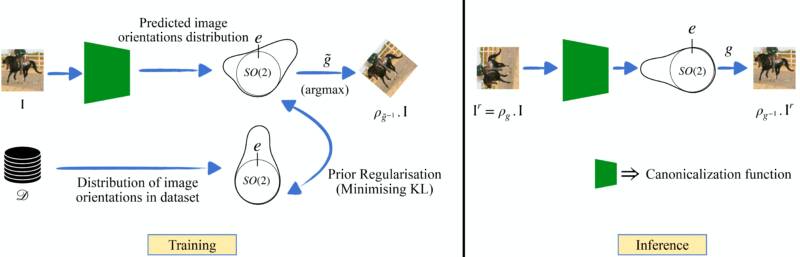
Place à l’a priori de canonisation

En termes simples, il s’agit d’une force directrice qui garantit que la fonction de canonisation se comporte et produit des données de sortie que le réseau de prédiction préentraîné attend et peut traiter. Nous nous appuyons sur l’idée que nos données peuvent fournir des indications sur les transformations « typiques » qu’elles subissent. En codant ces indications dans un a priori, nous pouvons orienter notre fonction de canonisation pour qu’elle produise des données transformées qui ne sont pas seulement standardisées, mais aussi alignées sur les données sur lesquelles le réseau de prédiction a été entraîné.

Bien que mathématique et complexe, l’ensemble de ce processus peut se résumer à s’assurer que le grand réseau de prédiction préentraîné examine toujours les échantillons de la distribution. Il en résulte un modèle très robuste, capable de gérer en toute confiance les diverses transformations des données d’entrée et de fournir des prédictions précises à tout coup. Nous montrons que cette notion peut s’appliquer à de grands modèles de fondation, comme le Segment Anything Model [6], pour les rendre robustes aux rotations tout en augmentant de façon optimale leur nombre de paramètres et leur vitesse d’inférence.

Conclusion

Dans le monde en constante évolution de l’IA et de l’apprentissage profond, il est essentiel de s’assurer que les modèles sont robustes et conscients des symétries. En apprenant à transformer intelligemment nos données d’entrée afin qu’elles prennent la bonne orientation pour les modèles préentraînés, nous pouvons créer des modèles à grande échelle puissants et conscients des transformations de données. Cela nous rapproche des systèmes d’IA qui comprennent le monde tout comme nous. Au fur et à mesure que la recherche sur la mise à l’échelle se poursuit, la fusion de grands modèles de fondation avec des techniques d’adaptation équivariantes comme celle-ci pourrait devenir une approche fondamentale pour améliorer la cohérence et la fiabilité des systèmes d’IA.

Références

1. Taco Cohen and Max Welling. Group equivariant convolutional networks. In Proceedings of The 33rd International Conference on Machine Learning, volume 48 of Proceedings of Machine Learning Research, pages 2990–2999, New York, New York, USA, 20–22 Jun 2016. PMLR
2. Daniel Worrall and Max Welling. Deep scale-spaces: Equivariance over scale. Advances in Neural Information Processing Systems, 32, 2019.
3. Michael M Bronstein, Joan Bruna, Taco Cohen, and Petar Velickovi ́c. Geometric deep learning: Grids, groups, graphs, geodesics, and gauges. arXiv preprint arXiv:2104.13478, 2021.
4. Rishi Bommasani, Drew A Hudson, Ehsan Adeli, Russ Altman, Simran Arora, Sydney von Arx, Michael S Bernstein, Jeannette Bohg, Antoine Bosselut, Emma Brunskill, et al. On the opportunities and risks of foundation models. arXiv preprint arXiv:2108.07258, 2021.
5. Sékou-Oumar Kaba, Arnab Kumar Mondal, Yan Zhang, Yoshua Bengio, and Siamak Ravanbakhsh. Equivariance with learned canonicalization functions. In 40th International Conference on Machine Learning, 2023.
6. Alexander Kirillov, Eric Mintun, Nikhila Ravi, Hanzi Mao, Chloe Rolland, Laura Gustafson, Tete Xiao, Spencer Whitehead, Alexander C. Berg, Wan-Yen Lo, Piotr Dollár, and Ross Girshick. Segment anything. In International Conference on Computer Vision, 2023.
7. Tsung-Yi Lin, Michael Maire, Serge Belongie, James Hays, Pietro Perona, Deva Ramanan, Piotr Dollár, and C Lawrence Zitnick. Microsoft coco: Common objects in context. In Computer Vision–ECCV 2014.

Citation

Pour plus de détails, consultez le document NeurIPS 2023. “Equivariant Adaptation of Large Pre-Trained Models.”

Pour les citations, merci d’utiliser ceci :

@inproceedings{
mondal2023equivariant,
title={Equivariant Adaptation of Large Pretrained Models},
author={Mondal, Arnab Kumar and Panigrahi, Siba Smarak and Kaba, S{\’e}kou-Oumar and Rajeswar, Sai and Ravanbakhsh, Siamak},
booktitle={Thirty-seventh Conference on Neural Information Processing Systems},
year={2023},
url={https://openreview.net/forum?id=m6dRQJw280}
}