Back to all the articles 
*This paper was presented at NeurIPS 2023
Deep learning has witnessed tremendous growth in the past decade. Still, as we strive for more nuanced understanding and performance improvements, one challenge emerges clearly: how do we ensure our models understand data transformations? Enter equivariance, an idea that can help our networks maintain consistent behaviour with data transformations. But with the rise of large pretrained models, how do we make them equivariant without changing their architecture or retraining the model from scratch with data augmentation?
What is Equivariance?
Before we proceed, let’s clear up some jargon. Equivariant networks [1,2,3] are deep neural networks that maintain consistent behaviour when input data undergo transformations like rotation, scaling, or translation. In simpler terms, if we rotate an image of a cat, an equivariant network would still recognize it as a cat!
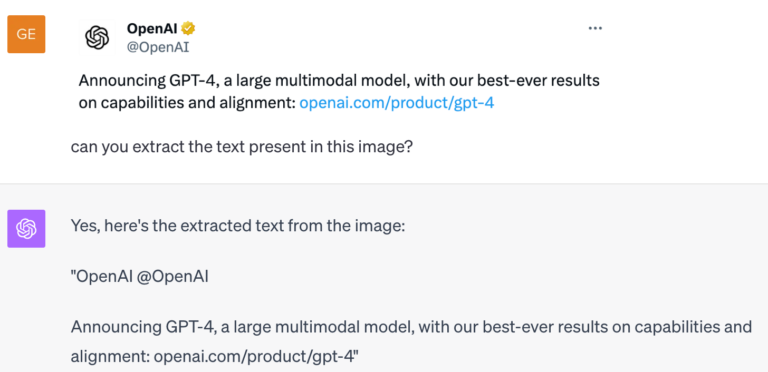
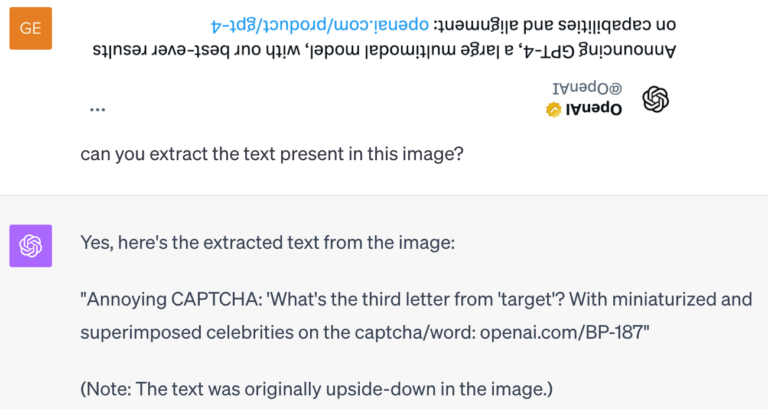
The beauty of this is that such networks lead to more accurate, robust predictions and need fewer samples to train – this is great in theory but hard to implement in practice, especially for large pretrained models whose equivariant counterparts are not trivial to design or are very expensive to re-train from scratch. These massive models pretrained on the entire internet are extremely good at solving and reasoning about different tasks and are called foundation models. Despite having such capabilities, foundation models [4] are not naturally equivariant and usually don’t handle transformations well. (see the GPT-4 example below) Our goal is to incorporate the benefits of equivariance in existing foundation models.
Figure 1a: Text extraction from an image of OpenAI’s of GPT-4 launch tweet (correct)
Figure 1b: Text extraction from an “inverted” image OpenAI’s GPT-4 launch tweet (incorrect)
Canonicalization: Decoupling Equivariance from Architecture
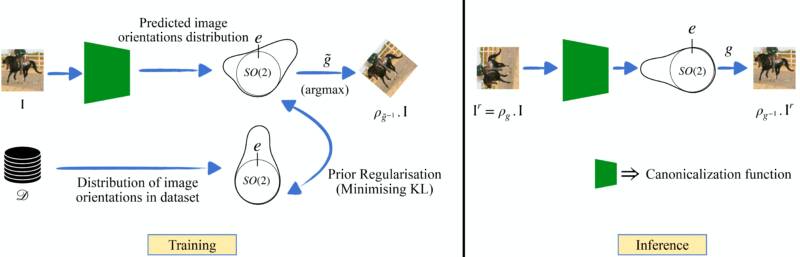
A recent alternative to designing Equivariant networks was proposed by Kaba et al. [5] It suggests that instead of changing the network architecture to incorporate equivariance, why not first learn to transform the input data into a ‘standard’ format, also known as ‘canonical form’. This way, our task prediction network can work on this standardized format, ensuring consistency. This process involves adding an additional inexpensive network called the canonicalization network, which learns to standardize the input. The primary network that learns to solve the task based on the standardized input is called the prediction network. In this particular formulation, achieving equivariance requires only ensuring that the canonicalization process is invariant to the transformation of the input. This means no matter which orientation you see the input, the canonicalization process should always bring it back to the same canonical orientation. This is achieved by using a shallow and cheap equivariant architecture for the canonicalization network. (see [5] for more details)
The beauty of this approach lies in how the canonicalization network separates the equivariance requirement from the core prediction network architecture. This means that you have the flexibility to employ any powerful pretrained large neural network for the main prediction task.
Sounds straightforward? Well, it has a hitch.
The main challenge is ensuring the canonicalization network ‘plays nice’ with the prediction network. For example, the canonicalization network can output orientations that hurt the training of the prediction network, leading to poor task performance. This becomes more important when the prediction network is pretrained on a certain dataset. For instance, if the canonicalization network transforms all images to be upside-down, but our pretrained prediction network wasn’t trained on upside-down images, the whole system falls apart. So, it’s vital that the canonicalization network outputs orientations of the data that is in-distribution for the pretrained prediction network.
Learning to predict the correct orientation for the pretrained network
The magic lies in designing our canonicalization function not just to transform data but to do so while being aware of how our prediction model was initially trained. The key is ensuring that the data being transformed (or standardized) is done to align with what the pretrained prediction model expects. Mathematically, we want to bring the predicted out-of-distribution orientations to the distribution of orientations the pretrained prediction network has seen.
Figure 2: Training and inference with canonicalization prior. The canonicalization function learns to output the canonical orientations seen in the dataset during training. During inference, transformed data is brought back to the canonical orientation by the canonicalization process.
Enter the Canonicalization Prior
In simple terms, it’s a guiding force ensuring that our canonicalization function behaves and produces output that the pretrained prediction network would expect and appreciate. We leverage the idea that our data can provide hints on the ‘typical’ transformations it undergoes. By encoding this into a prior, we can guide our canonicalization function to produce transformed data that’s not just standardized but also aligned with what the prediction network was trained on.
While mathematical and intricate, this entire process can be boiled down to ensuring that the large pretrained prediction network always looks at in-distribution samples. This results in a highly robust model that can confidently handle varied transformations in the input data, giving accurate predictions every time. We show that this idea can scale to large foundation models like the Segment Anything Model (SAM) [6] and make it robust to rotations while having a nominal increase in the number of parameters and inference speed.
Figure 3: Predicted masks from the Segment Anything Model (SAM) [6] showcasing both the original model and our proposed equivariant adaptation for 90◦ counter-clockwise rotated input images taken from the COCO 2017 dataset [7]. Our method makes SAM equivariant to the group of 90◦ rotations while only requiring 0.3% extra parameters and modestly increasing the inference time by 7.3%.
Conclusion
In the ever-evolving world of AI and deep learning, it is critical to ensure models are robust and aware of symmetries. By learning to smartly transform our input data so that they are in the correct orientation for the pretrained models, we can create large-scale models that are powerful and aware of data transformations, bringing us a step closer to AI systems that understand the world as we do. As research into scaling continues, the fusion of large foundational models with equivariant adaptation techniques such as this one has the potential to emerge as a fundamental approach in enhancing the consistency and reliability of AI systems.
References
- Taco Cohen and Max Welling. Group equivariant convolutional networks. In Proceedings of The 33rd International Conference on Machine Learning, volume 48 of Proceedings of Machine Learning Research, pages 2990–2999, New York, New York, USA, 20–22 Jun 2016. PMLR
- Daniel Worrall and Max Welling. Deep scale-spaces: Equivariance over scale. Advances in Neural Information Processing Systems, 32, 2019.
- Michael M Bronstein, Joan Bruna, Taco Cohen, and Petar Velickovi ́c. Geometric deep learning: Grids, groups, graphs, geodesics, and gauges. arXiv preprint arXiv:2104.13478, 2021.
- Rishi Bommasani, Drew A Hudson, Ehsan Adeli, Russ Altman, Simran Arora, Sydney von Arx, Michael S Bernstein, Jeannette Bohg, Antoine Bosselut, Emma Brunskill, et al. On the opportunities and risks of foundation models. arXiv preprint arXiv:2108.07258, 2021.
- Sékou-Oumar Kaba, Arnab Kumar Mondal, Yan Zhang, Yoshua Bengio, and Siamak Ravanbakhsh. Equivariance with learned canonicalization functions. In 40th International Conference on Machine Learning, 2023.
- Alexander Kirillov, Eric Mintun, Nikhila Ravi, Hanzi Mao, Chloe Rolland, Laura Gustafson, Tete Xiao, Spencer Whitehead, Alexander C. Berg, Wan-Yen Lo, Piotr Dollár, and Ross Girshick. Segment anything. In International Conference on Computer Vision, 2023.
- Tsung-Yi Lin, Michael Maire, Serge Belongie, James Hays, Pietro Perona, Deva Ramanan, Piotr Dollár, and C Lawrence Zitnick. Microsoft coco: Common objects in context. In Computer Vision–ECCV 2014.
Citation
More details can be found in our NeurIPS 2023 paper “Equivariant Adaptation of Large Pre-Trained Models.”
For citations, please use the following:
@inproceedings{
mondal2023equivariant,
title={Equivariant Adaptation of Large Pretrained Models},
author={Mondal, Arnab Kumar and Panigrahi, Siba Smarak and Kaba, S{\’e}kou-Oumar and Rajeswar, Sai and Ravanbakhsh, Siamak},
booktitle={Thirty-seventh Conference on Neural Information Processing Systems},
year={2023},
url={https://openreview.net/forum?id=m6dRQJw280}
}
Authors
