Introduction
Les prédictions des modèles d’IA touchent de plus en plus la vie de tout le monde : les résultats de recherche, les recommandations d’achat, les évaluations de prêts, et la sélection de CV lors d’un recrutement sont autant d’exemples.
Pour s’assurer que ces systèmes automatiques se comportent de manière appropriée et ne causent pas de dommages, il est nécessaire d’expliquer ce en quoi consiste la prédiction de l’IA. Par exemple, quels mots de la requête ont été déterminants pour la prédiction? De nombreuses approches ont été adoptées pour répondre à cette question. Toutefois, il a déjà été constaté qu’aucune d’entre elles ne fonctionnait de manière systématique [1]. Il est extrêmement difficile d’arriver à cette conclusion, car nous ne savons pas à quoi ressemble une explication vraie.
Dans cette étude, nous proposons une nouvelle orientation dans ce domaine : la mise au point de modèles dotés d’un mécanisme intégré permettant de déterminer si une explication est vraie, ce que l’on appelle les modèles mesurables de fidélité (Faithfulness Measurable Models). Puisque ce mécanisme est intégré, il est très peu coûteux à utiliser, et il produit des résultats précis. Il nous permet également de trouver l’explication optimale à partir d’une prédiction, ce qui était impossible auparavant. Il en résulte que les explications reflètent de manière systématique le comportement du modèle et sont de deux à cinq fois plus précises qu’avant.

Les modèles mesurables de fidélité
L’idée centrale permettant de déterminer si une explication reflète le modèle est que si l’on supprime des mots prétendument importants, la prédiction du modèle devrait changer beaucoup, particulièrement davantage que si l’on supprime des mots au hasard. Dans le contexte du texte, la suppression est souvent effectuée en remplaçant le texte par un segment de masque spécial.
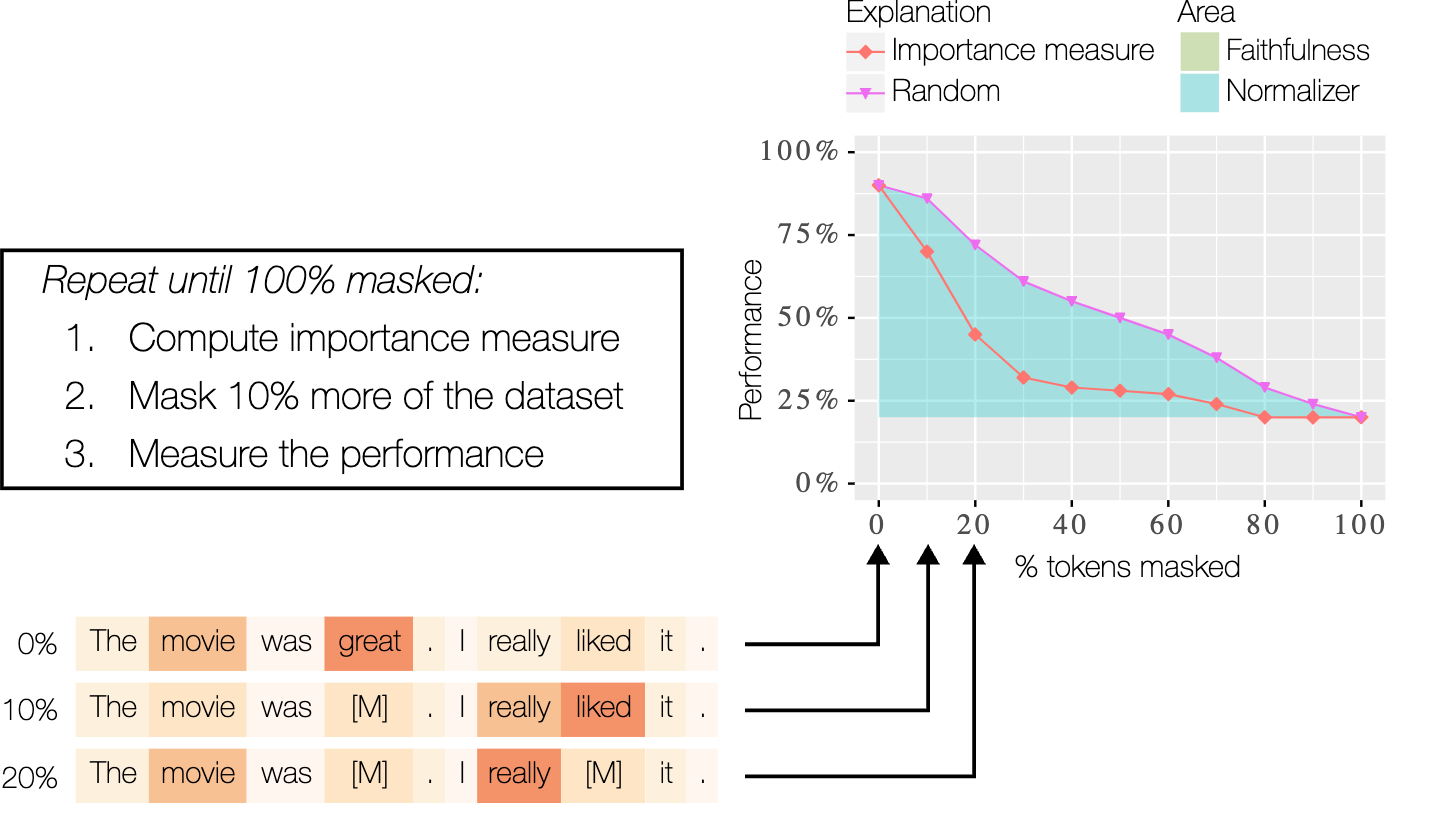
Malheureusement, il est impossible de se contenter de masquer les mots, car cela crée des entrées non grammaticales, avec lesquelles un modèle typique ne peut pas fonctionner. Des études antérieures ont résolu ce problème en réentraînant le modèle sur les ensembles de données partiellement masqués [1]. Toutefois, cette opération est coûteuse, car le modèle doit être réentraîné 10 fois pour chaque ensemble de données et chaque explication analysée. De plus, cela signifie que nous nous éloignons du modèle en cours de déploiement parce que nos mesures reposent désormais sur un modèle différent. Cela rend cette méthode de réentraînement à la fois difficile à appliquer et potentiellement dangereuse, car elle peut induire une confiance erronée envers une explication.
Nous nous trouvons donc entre le marteau et l’enclume. D’une part, si le modèle ne soutient pas la suppression ou le masquage, cela crée une mesure erronée. D’autre part, si nous ré-entraînons le modèle pour qu’il soutienne la suppression ou le masquage, cela crée également une mesure erronée. La solution à ce problème est la suivante : et si nous disposions d’un seul modèle qui soutient la suppression ou le masquage dès le départ?
Un tel modèle constitue l’idée centrale de cet article; de plus, il est étonnamment facile à réaliser. Pour ce faire, il faut masquer la moitié de l’ensemble de données d’entraînement de manière aléatoire, avec un taux de masquage compris entre 0 % et 100 %. Ainsi, le modèle apprend à faire des prédictions normales, mais aussi des prédictions lorsque l’entrée a été masquée. Nous appelons cette idée « peaufinage masqué » et la visualisons dans la figure 2.
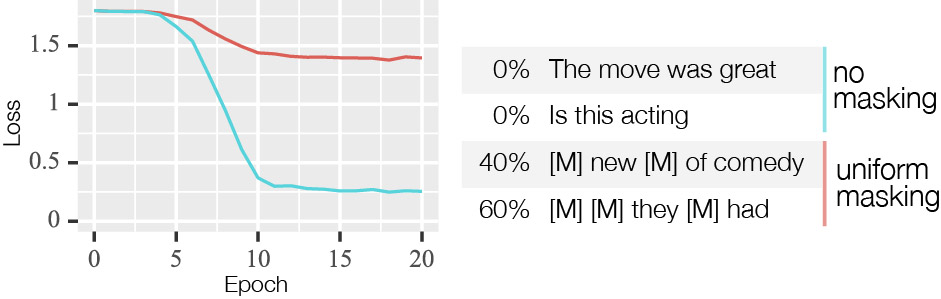
Pour vérifier que cela fonctionne, à la fois en termes d’absence d’incidence sur la performance normale et de soutien au masquage, nous effectuons un certain nombre de tests. Premièrement, nous montrons qu’il n’y a pas de perte de performance en utilisant un peaufinage masqué par rapport à un peaufinage ordinaire, dans lequel aucun masquage n’est effectué. Nous le démontrons à travers 16 ensembles de données de traitement du langage naturel. Deuxièmement, à titre de vérification simple du soutien offert par le masquage, nous remplaçons tous les mots par le segment de masque spécial. Lorsque le masquage est à 100 %, nous ne savons pratiquement rien de l’entrée, de sorte que le mieux que le modèle puisse faire est de prédire la classe qui apparaît le plus souvent (appelée « point de référence de la classe majoritaire »). Nous démontrons que ce n’est que lorsque le masquage est utilisé que la performance des modèles correspond à ce point de référence.
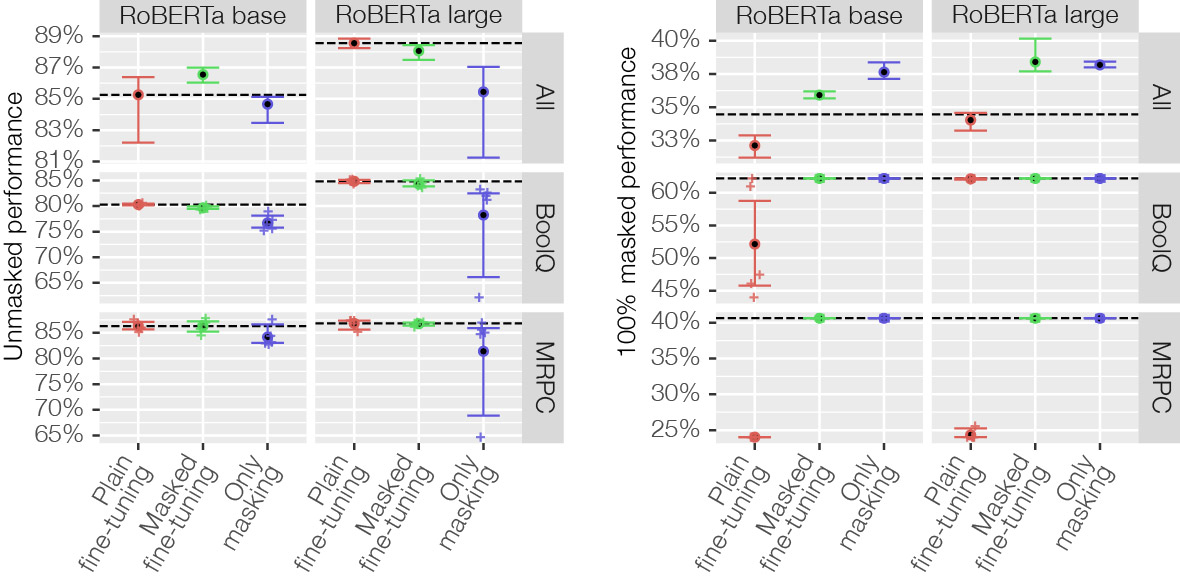
Les résultats de la figure 3 confirment que le modèle fonctionne pour des entrées masquées à 0 % et à 100 %. Mais qu’en est-il de tout ce qui se trouve entre les deux? Pour ces niveaux de masquage, nous ne savons pas à quelle performance nous attendre. Pour résoudre ce problème, nous effectuons un test statistique afin de vérifier si le modèle se comporte comme il le ferait normalement. Le test que nous appliquons s’appelle MaSF [2], dont les détails sont trop compliqués pour être abordés dans ce billet de blogue. En bref, il s’agit d’observer les activations intermédiaires du modèle pour l’ensemble des données de validation, puis à vérifier si les activations obtenues à partir d’une nouvelle observation se situent à l’intérieur de cette plage d’activation. Néanmoins, les résultats de la figure 4 montrent que l’application du peaufinage masqué ne pose jamais de problème, tandis que lorsque l’on applique le peaufinage ordinaire, certains ensembles de données présentent des problèmes où le modèle ne fonctionne pas.
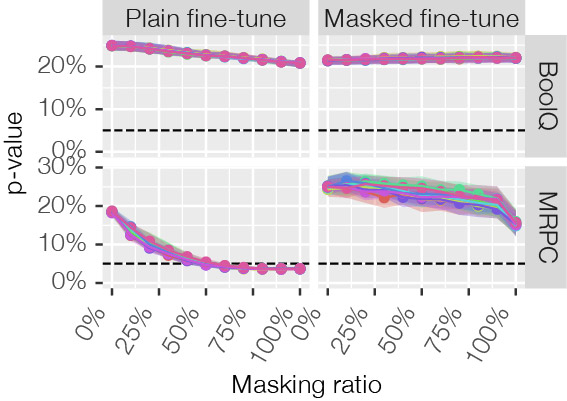
Maintenant que nous savons que le modèle se comporte comme souhaité, nous pouvons mesurer si les explications reflètent ce modèle. Pour rappel, l’idée centrale est que si l’on supprime des mots importants, la prédiction du modèle devrait changer beaucoup, particulièrement davantage que si l’on supprime des mots au hasard. Les résultats de la figure 5 illustrent clairement que Leave-one-out (LOO) et Beam [3] sont les plus performants. Cela se justifie puisqu’ils tirent parti du soutien offert par le masquage, ce qui n’est pas le cas des autres méthodes d’explication. Beam est particulièrement intéressant, car il détermine l’explication qui reflète le plus fidèlement possible le comportement du modèle à l’aide d’une méthode d’optimisation. Cela est possible parce que le modèle mesurable de fidélité permet de le déterminer à peu de frais et de manière efficace. Les détails [3] ne sont pas importants pour ce billet de blogue, mais l’essentiel est de considérer chaque mot comme le mot le plus important, de mesurer la qualité de chacune de ces explications, puis de sélectionner les trois meilleures explications (ou d’en choisir un nombre quelconque). Ensuite, pour ces trois explications, on identifie le deuxième mot le plus important et ainsi de suite, en conservant toujours les trois meilleures explications candidates jusqu’à ce que le meilleur classement de l’importance de tous les mots soit établi. Puisque seules les trois meilleures explications sont prises en compte, il s’agit d’une méthode approximative. Elle n’est pas toujours la meilleure, mais elle l’est souvent.
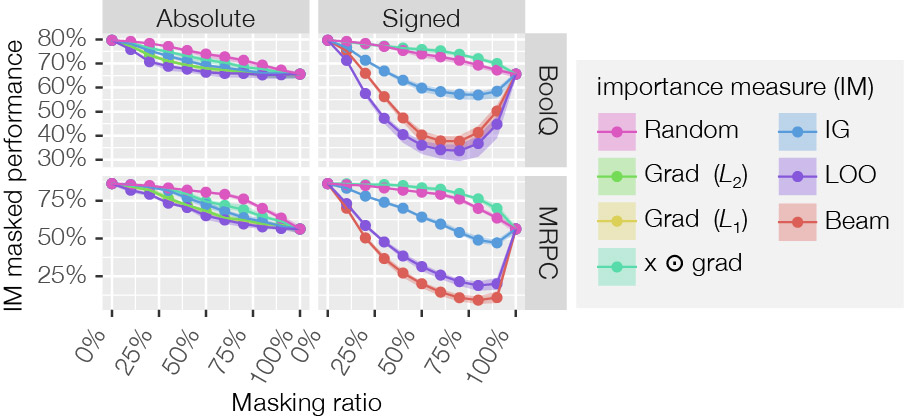
Il est possible de quantifier dans quelle mesure la courbe d’explication se situe en dessous de la courbe aléatoire d’explication en calculant l’aire entre les courbes. Pour les explications absolues, c’est-à-dire celles qui ne peuvent pas faire la distinction entre les mots contribuant positivement et ceux contribuant négativement, ce chiffre peut ensuite être normalisé par l’explication théorique optimale, comme le montre la figure 1. Cela facilite la comparaison avec d’autres méthodes et modèles, en l’occurrence avec le modèle ROAR récursif, qui a recours au réentraînement [1].
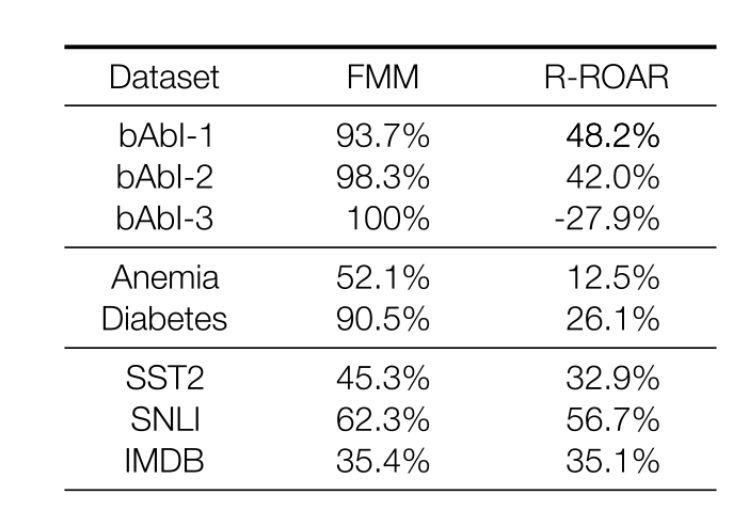
Le résultat de cette comparaison est indiqué dans le tableau 1. Ici, nous observons souvent une amélioration de deux à cinq fois. Cependant, nous avons surtout constaté que certaines explications reflètent de manière systématique le comportement du modèle, ce qui n’était pas le cas auparavant, et que pour des ensembles de données synthétiques comme (bAbI), les explications se rapprochent de la perfection théorique.
Conclusion
Grâce à une modification simple de la manière dont les modèles sont habituellement peaufinés, nous sommes en mesure de créer un modèle dans lequel il est possible de mesurer à peu de frais et avec précision à quel point une explication reflète le véritable comportement du modèle, ce qui permet d’optimiser les explications en vue d’une vérité maximale. Nous appelons un tel modèle un modèle mesurable de fidélité.
En outre, nous constatons que les explications actuelles reflètent de manière systématique le comportement du modèle, qu’elles sont de deux à cinq fois plus précises et qu’elles peuvent fonctionner avec une quasi-perfection théorique. Enfin, la procédure modifiée de peaufinage n’a pas d’incidence sur la performance, ce que nous avons vérifié sur 16 ensembles de données.
Références
[1] Madsen, A., Meade, N., Adlakha, V., & Reddy, S. (2022). Evaluating the Faithfulness of Importance Measures in NLP by Recursively Masking Allegedly Important Tokens and Retraining. Findings of the Association for Computational Linguistics: EMNLP 2022, 1731–1751. https://aclanthology.org/2022.findings-emnlp.125
[2] Matan, H., Frostig, T., Heller, R., & Soudry, D. (2022). A Statistical Framework for Efficient Out of Distribution Detection in Deep Neural Networks. International Conference on Learning Representations. https://openreview.net/forum?id=Oy9WeuZD51
[3] Zhou, Y., & Shah, J. (2023). The Solvability of Interpretability Evaluation Metrics. Findings of the Association for Computational Linguistics: EACL. http://arxiv.org/abs/2205.08696