Au 20e siècle, les progrès des connaissances biologiques et de la médecine fondée sur des données probantes ont été systématiquement étayés par des valeurs p et des méthodes connexes. Les valeurs p et les tests d’hypothèse nulle sont depuis longtemps acceptés comme la référence en matière de prise de décision clinique et de politique de santé publique. Pourtant, le tournant du siècle remet en question cette approche préconisant « un médicament pour tous ». Au cours des dernières années, l’essor de la médecine de précision a mis l’accent sur les soins de santé personnalisés et sur des prédictions précises pour chaque patient. Ce changement de paradigme provoque des tensions entre les méthodes de régression traditionnelles utilisées pour inférer des différences de groupe statistiquement significatives et les outils d’analyse prédictive en plein essor, adaptés pour prévoir l’évolution de la santé d’un individu à un moment ultérieur. Dans un avenir où les prédictions pour un patient unique reposeront sur des mégadonnées biomédicales, il pourrait devenir essentiel que la modélisation pour l’inférence et la modélisation pour la prédiction soient à la fois liées et différentes.
Dans cet article, nous discutons de notre étude, « Inference and Prediction in Biomedicine » (Inférence et prédiction en biomédecine), qui sera publiée dans Patterns, une revue en libre accès de Cell Press. Notre comparaison fait appel à des modèles linéaires pour cerner les variables contributives importantes et pour trouver les ensembles de variables les plus prédictifs. En appliquant des simulations de données systématiques et des ensembles de données médicales communes, nous montrons que des conclusions divergentes peuvent se dégager même lorsque les données sont identiques et lorsque des modèles linéaires très répandus sont utilisés. La prise de conscience des forces et faiblesses relatives des deux « cultures d’analyse des données » peut donc devenir cruciale pour la recherche reproductible, avec des implications potentielles pour l’avancement des soins médicaux personnalisés.
Si vous modifiez votre philosophie en matière de statistiques, différentes choses deviennent soudainement plus importantes.
À l’interface de l’apprentissage automatique et des statistiques classiques en biomédecine
Les outils d’analyse de régression ont longtemps été utilisés dans la recherche biomédicale. Cependant, les mêmes outils d’analyse de régression sont souvent associés à des objectifs non identiques au sein de différentes communautés scientifiques. En revanche, le déluge de données qui s’accélère en biologie et en médecine a conduit au développement de nouvelles sortes d’approches de modélisation, comme les algorithmes de prédiction flexibles, qui sont bien adaptés pour passer au crible des données riches afin d’extraire des modèles subtils en médecine. En raison de ces récents progrès dans les algorithmes d’apprentissage automatique, la recherche clinique appliquée s’est tournée vers la combinaison de mesures hétérogènes et riches provenant de différentes sources pour la prévision par « force brute » de paramètres utiles sur le plan pratique, comme la prédiction de la durée d’hospitalisation de nouveaux patients à partir de dossiers médicaux électroniques antérieurs.
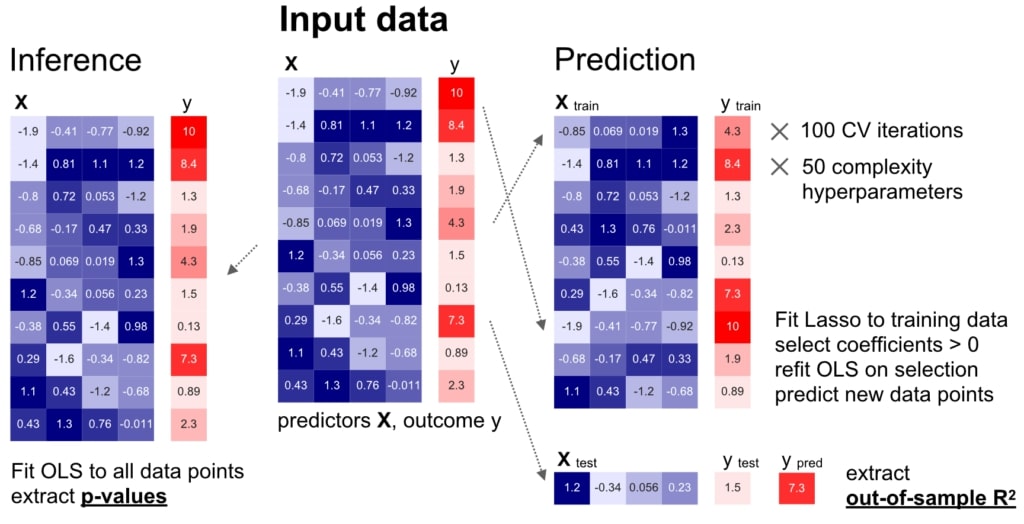
Nous avons procédé à une comparaison minutieuse de la modélisation pour l’inférence (à gauche) et de la modélisation pour la prédiction (à droite) sur des ensembles de données identiques, à partir de simulations empiriques complètes et d’ensembles de données biomédicales du monde réel.
Pendant longtemps, ces utilisations disparates d’outils d’analyse identiques ont été effectuées en parallèle avec peu de dialogue entre les communautés. Par conséquent, la relation empirique entre le programme établi d’inférence statistique et le programme maintenant en expansion de performance de prédiction à partir d’algorithmes d’apprentissage automatique reste largement obscure. Par conséquent, notre recherche empirique systématique vise à réunir dans un même tableau les outils analytiques de l’inférence classique et de la prédiction de modèles, en mettant en évidence leurs points communs et leurs différences caractéristiques.
Simulation de données empiriques
Notre approche en matière de simulation de données nous a fourni un contrôle précis sur cinq dimensions clés des ensembles de données, ce qui a permis de comparer minutieusement :
- La taille de l’échantillon disponible
- Le nombre de variables d’entrée informatives
- La redondance des données contenues dans les variables d’entrée relatives au résultat
- La variation aléatoire du bruit
- La spécification erronée du modèle quantitatif
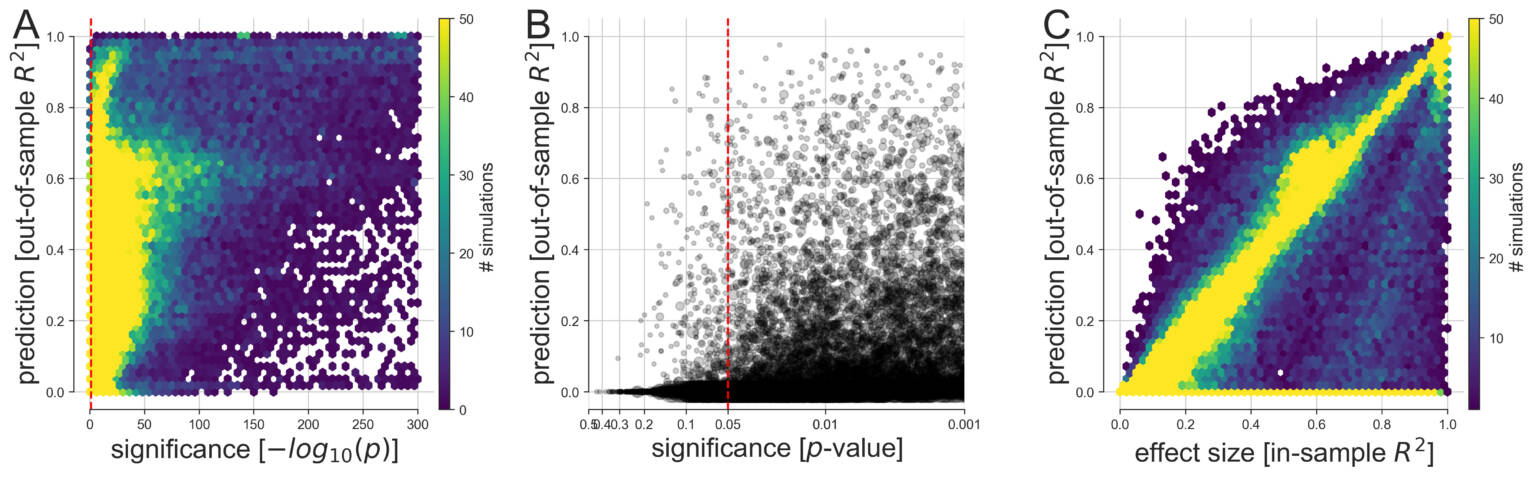
(A) À partir de 113 400 simulations, l’écart entre la modélisation prédictive et la modélisation explicative a été quantifié dans un large éventail de cas d’analyse de données possibles. Les variables et les résultats générés ont été analysés par des modèles linéaires dans le but de tirer une inférence classique (meilleure valeur p parmi tous les coefficients, axe des X) et d’évaluer la performance de prévision du modèle sur des données jamais vues (score R2, hors échantillon, de l’ensemble du modèle, axe des Y). Nous avons ensuite conçu plusieurs visualisations pour donner un aperçu des facettes complémentaires de cette collection de résultats de simulation.
(B) La précision prédictive et la signification statistique sont juxtaposées à une échelle affinée avec leur relation aux seuils communément appliqués à p < 0,05, p < 0,01, et p < 0,001 (un cercle gris plus grand signifie un échantillon de plus grande taille).
(C) Comme les valeurs p plus petites ne représentent pas une preuve statistique plus probante, la précision de la prédiction est comparée à la taille de l’effet dérivée de la variance expliquée sur les données du calage du modèle (score R2, faisant partie de l’échantillon, du modèle). Dans la grande majorité des analyses de données effectuées, au moins une variable d’entrée était significativement liée à la variable dépendante à p < 0,05 (ligne verticale pointillée rouge). Cependant, à partir des mêmes données, nous avons observé une dispersion considérable dans la mesure où des modèles linéaires aussi importants étaient capables de faire des prédictions utiles sur des observations récentes. Notez que les plus petites valeurs p se situent dans la fourchette inférieure au plus petit nombre à virgule flottante de 64 octets autour de 2.2 x 10-308 qui peut être représenté dans Python. De telles valeurs p sont conceptuellement plausibles et peuvent se produire dans de grands ensembles de données simulées, par exemple lorsque de nombreux prédicteurs expliquent le résultat et lorsqu’il n’y a pas de bruit.
Sur 113 400 ensembles de données simulées, nous avons calculé toutes les combinaisons possibles en utilisant une approche « par force brute » et avons observé plusieurs différences caractéristiques entre la recherche d’inférence statistique et la maximisation de la prédiction à partir d’algorithmes d’apprentissage des formes. Dans la figure 3, nous détaillons la manière dont la modélisation linéaire pour les tests d’hypothèse et la modélisation linéaire pour la prédiction concordaient et divergeaient dans les ensembles de données construites. À l’aide des cinq ensembles de données, nous avons reproduit les défis et les scénarios fréquemment rencontrés auxquels les chercheurs font face au quotidien, comme l’augmentation du bruit dans les données et l’augmentation de la corrélation partagée entre les mesures d’entrée.
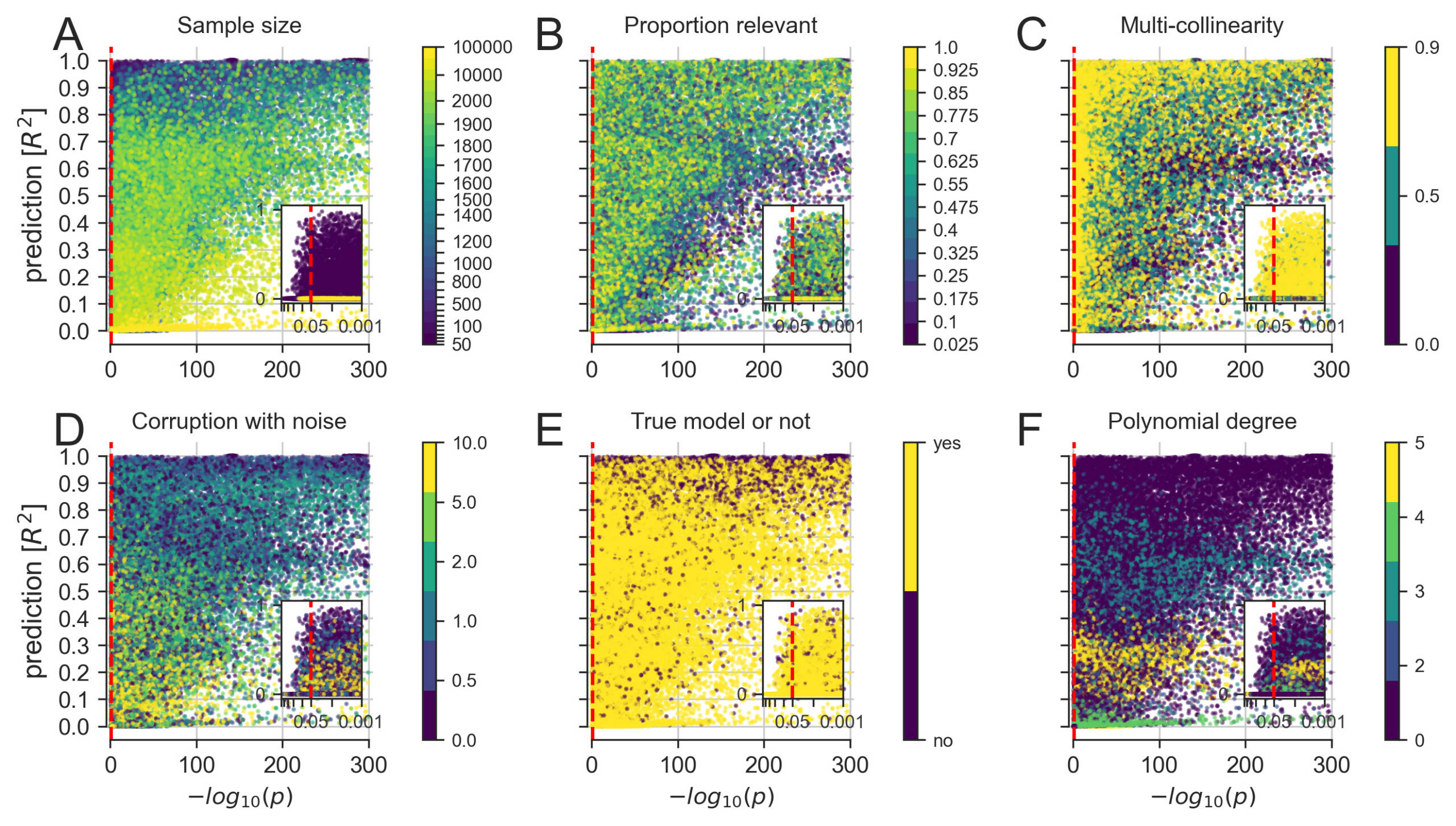
Une exploration plus détaillée de la manière dont la modélisation linéaire pour les tests d’hypothèse (meilleure valeur p parmi tous les coefficients, axe des X) et la modélisation linéaire pour la prédiction (score R2, hors échantillon, de l’ensemble du modèle, axe des Y) concordaient et divergeaient dans les ensembles de données construits.
(A) L’augmentation du nombre de points de données disponibles a finalement donné lieu à des cooccurrences de grande signification et de grande prédiction.
(B) Un petit nombre de prédicteurs pertinents a permis d’établir des scénarios avec des valeurs p très importantes combinées à une faible performance prédictive.
(C) Il semblerait qu’augmenter la corrélation entre les mesures d’entrée, courantes dans les données biologiques, entraîne une dégradation des valeurs p plus importante que la performance sur le plan de la prédiction.
(D) Il semblerait qu’augmenter la variation aléatoire des données, qui peut être considérée comme une imitation des erreurs de mesure, réduise plus systématiquement la prévisibilité que la signification.
(E) Les contextes pathologiques, où le modèle choisi ne correspond pas au processus de génération de données de la collecte des variables d’entrée et de sortie, peuvent améliorer à la fois la signification et la prédiction.
(F) L’ajustement d’un modèle linéaire à des données aux effets non linéaires croissants a permis d’atteindre facilement un niveau de signification, mais la prévisibilité des résultats a varié de manière distincte
Nos résultats révèlent une série d’incongruités dans l’identification des variables importantes parmi un ensemble de variables candidates. À l’aide de modèles linéaires, la signification statistique et des prédictions précises ont montré des modèles divergents de réussite dans la détection des variables que nous savions pertinentes pour le résultat. Pour chaque ensemble de données, la récupération calculée en fonction du sous-ensemble de coefficients des moindres carrés ordinaires correctement détectés comme étant significatifs et des coefficients actifs (c’est-à-dire non nuls) du modèle Lasso pertinents pour la prédiction du résultat. Des désaccords systématiques entre l’inférence et la prédiction sont apparus dans un certain nombre de cas en fonction de la taille de l’échantillon disponible et du nombre de variables pertinentes.
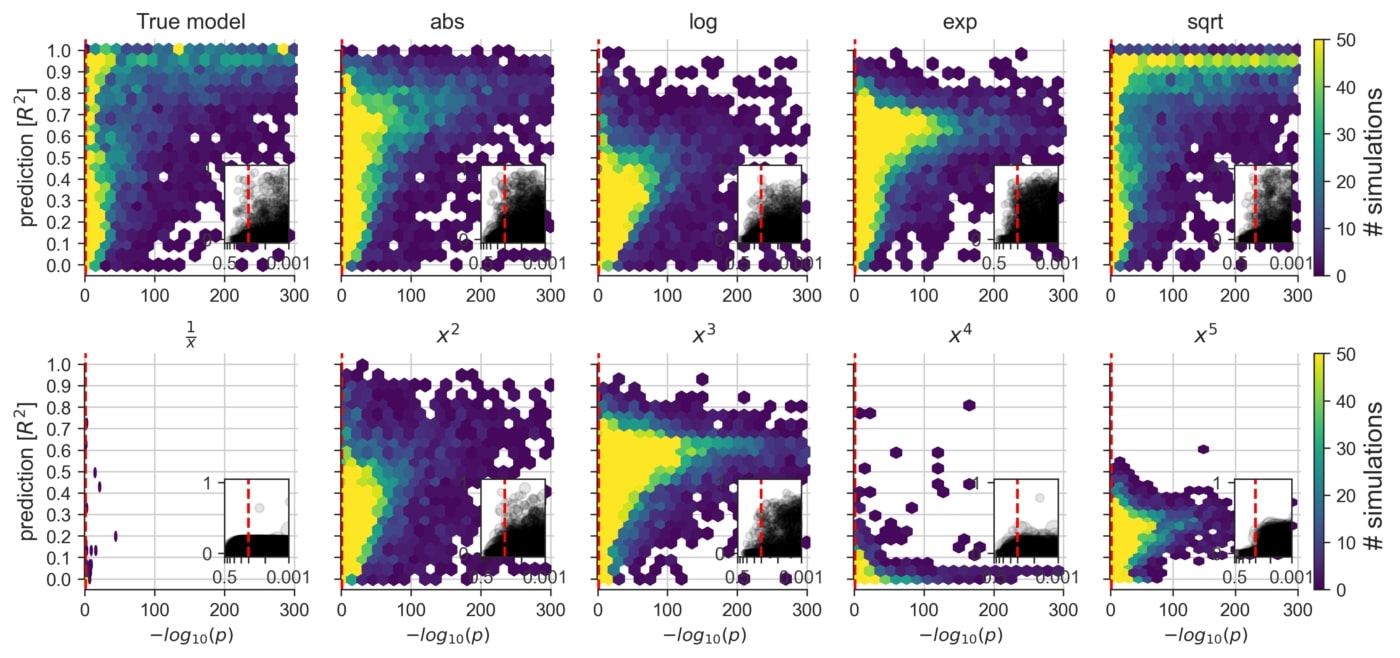
Une exploration des conséquences de l’application d’un modèle linéaire à des ensembles de données connus pour contenir des mécanismes de données non linéaires de différents types et degrés (voir la figure 2F). Certains effets non linéaires sont susceptibles d’influencer les mesures de divers systèmes biologiques du monde réel. Autrement dit, dans l’analyse quotidienne des données, un certain désalignement entre les données et le modèle linéaire couramment utilisé est susceptible de constituer la règle plutôt que l’exception.
En comparant le modèle Lasso et les moindres carrés ordinaires dans divers ensembles de données synthétiques, nous avons observé les plus grands désaccords dans l’identification des variables dans les ensembles de données dont les tailles d’échantillon sont petites ou modérées, ce qui est encore très courant dans l’analyse quotidienne des données biomédicales. Ainsi, nos résultats montrent que les chercheurs étaient plus souvent d’accord quant au choix entre les modèles linéaires pour la prédiction et les modèles linéaires pour l’inférence lorsque l’échantillon comprenait plus de 1 000 points de données. Pourtant, nous signalons que certains désaccords sont survenus même lorsque le nombre de points de données était supérieur ou égal à 10 000.
Ensembles de données médicales du monde réel
Pour ajouter un complément à la partie de cette étude consacrée à la simulation des données empiriques, nous avons effectué la même comparaison directe entre la modélisation explicative et la modélisation prédictive dans des ensembles de données communes du monde réel, comme le montre la figure 9. La réévaluation quantitative est présentée pour quatre ensembles de données médicales du monde réel populaires dans l’enseignement de l’analyse des données : poids à la naissance, cancer de la prostate, diabète et volume expiratoire maximal. Un aperçu complet des résultats des ensembles de données biomédicales se trouve sur le site Web de Cell Press et sera publié dans le numéro de novembre à paraître de la revue Patterns.
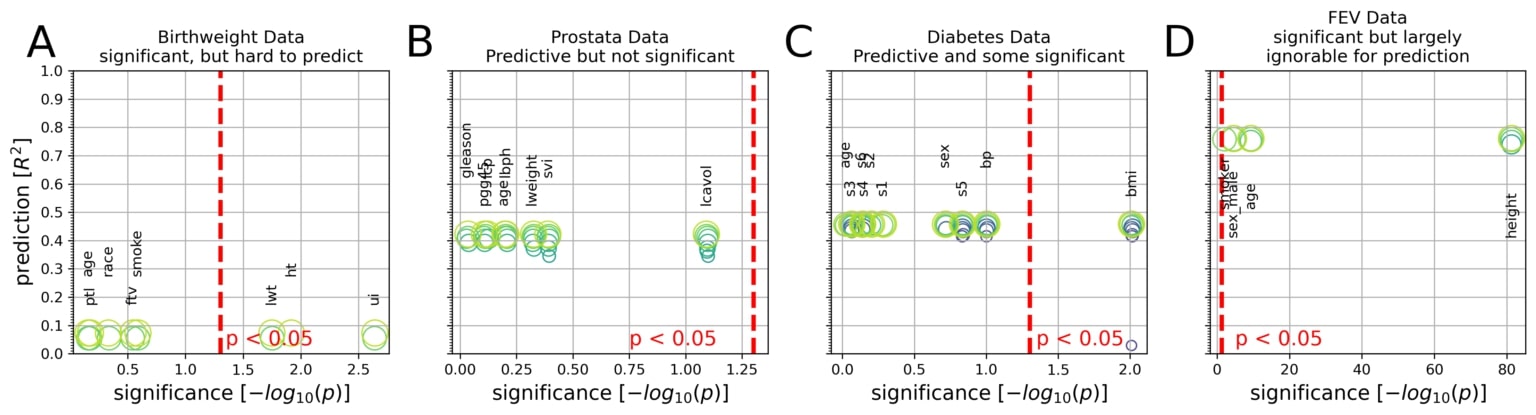
Les graphiques intégratifs représentent l’importance inférentielle de chaque coefficient de modèle linéaire (valeurs p sur l’axe des X, ayant subi une transformation logarithmique) et l’importance prédictive des ensembles de coefficients (scores R2, hors échantillon, sur l’axe des Y, obtenus à partir de l’application du modèle sur des données non utilisées pour le calage du modèle).
(A) Le poids corporel doit être calculé à partir de huit mesures chez 189 nouveau-nés. Trois mesures sur huit sont associées de manière statistiquement significative au poids à la naissance à p < 0,05 (ligne rouge). Cependant, l’utilisation du modèle linéaire pour la prédiction n’explique que 8 % de la variance observée chez les nouveau-nés (R2 = 0,08).
(B) L’antigène spécifique de la prostate, une molécule pour le dépistage du carcinome de la prostate, doit être dérivé de huit mesures chez 87 hommes. Aucun des huit coefficients n’a atteint une signification statistique fondée sur la régression linéaire commune, bien que les coefficients ajustés du modèle prédictif aient atteint une variance expliquée de 42 % chez les hommes non vus.
(C) La progression de la maladie après 1 an doit être calculée à partir de 10 mesures chez 442 patients diabétiques. L’indice de masse corporelle a fourni le seul coefficient significatif (p = 0,01), ce qui, seul, n’explique toutefois qu’environ 3 % de la progression de la maladie chez les futurs patients. Les coefficients complets du modèle prédictif atteignent un taux de variance expliquée de 46 % chez les patients indépendants.
(D) La capacité pulmonaire, quantifiée par le volume expiratoire maximal, doit être calculée à partir de quatre mesures chez 654 personnes en bonne santé. Toutes les mesures ont facilement dépassé le seuil de signification statistique. Cependant, un modèle prédictif intégrant uniquement la taille du corps a donné des résultats pratiquement identiques aux prédictions fondées sur les quatre coefficients (R2 = 0,74 vs R2 = 0,76).
Pour exposer le compromis entre parcimonie et performance de prédiction, les cercles (verts) montrent les ensembles de coefficients Lasso à différents niveaux de parcimonie. En résumé, les modèles linéaires peuvent montrer toutes les combinaisons de prédictif vs non prédictif et de significatif vs non significatif dans l’analyse des données biomédicales.
Implications pratiques
Notre recherche quantitative révèle comment des modèles quantitatifs largement utilisés peuvent être employés avec des motivations distinctes et partiellement incompatibles. Bien que la mise en œuvre de ces outils analytiques à des fins d’inférence soit utile pour découvrir les caractéristiques des processus biologiques et que l’utilisation de la modélisation prédictive linéaire soit bien adaptée à la prévision pragmatique des processus biologiques, il devient maintenant essentiel pour les professionnels de la santé et les chercheurs de reconnaître les philosophies de modélisation en partie incongrues qui consistent à tirer des inférences statistiques et à rechercher des algorithmes de prédiction.
À l’approche des futurs progrès de la médecine personnalisée, il devient essentiel que la modélisation pour l’inférence et la modélisation pour la prédiction soient liées, mais surtout différentes. Nous avons démontré, grâce à nos simulations empiriques et à nos ensembles de données biomédicales du monde réel, que des conclusions divergentes peuvent se dégager, même lorsque les données sont les mêmes et que l’on a recours à des modèles linéaires très répandus. En raison de la disponibilité croissante et exponentielle des mégadonnées médicales pouvant être exploitées dans le cadre de l’apprentissage automatique, et parce qu’il existe un écart, il est maintenant primordial de comprendre comment ces prédictions d’apprentissage automatique se situent dans le paysage plus large, car cela concerne toutes les disciplines médicales et l’avenir de la prise de décision clinique et des décisions en matière de politiques de santé publique.
Pour en savoir plus
Ce billet de blogue est fondé sur notre récent article publié sur le site Web de Cell Press :
L’inférence et la divergence des prédictions en biomédecine
Danilo Bzdok, Denis Engemann et Bertrand Thirion
Article en libre accès : https://www.cell.com/patterns/fulltext/S2666-3899(20)30160-4
- Pour explorer les plus de 100 000 résultats de simulation en temps réel portant sur la relation entre l’inférence et la prédiction, consultez notre WebApp (avec My Binder) ici.
- Tous les scripts d’analyse et les données nécessaires qui reproduisent les résultats de la présente étude sont facilement accessibles sur Github ici. À noter qu’ils peuvent être réutilisés.
Références
[1] Yau, T. O. (2019). Precision Treatment in Colorectal Cancer: Now and the Future. Journal of Gastroenterology and hepatology, 3, 361-369. https://onlinelibrary.wiley.com/doi/epdf/10.1002/jgh3.12153
[2] Effron, B. & Hastie, T. (2016). Computer Age Statistical Inference. Cambridge University Press).