Introduction
Le monde qui nous entoure est tridimensionnel, mais la vision, l’un des principaux moyens que nous avons d’observer le monde, est fortement tributaire des représentations bidimensionnelles. Il en va ainsi tant pour le sens de la vue que pour la vision artificielle. C’est pourquoi l’histoire de l’apprentissage automatique et de l’apprentissage profond est jalonnée d’avancées décisives impliquant des données d’imagerie 2D. Le recours à des réseaux de neurones convolutifs profonds pour obtenir une performance jamais vue lors du Défi ImageNet 2012 a donné un coup de projecteur au domaine de l’apprentissage profond. Plus récemment, des modèles génératifs d’images et de vidéos tels que DALL-E et Sora d’OpenAI ont déclenché une petite révolution culturelle.
Dans les prochaines années, grâce aux percées de l’informatique visuelle différentiable, de nombreuses technologies révolutionnaires d’apprentissage automatique passeront de la deuxième à la troisième dimension. Ces innovations auront des répercussions dans divers secteurs touchant à la détection d’objets 3D et à l’interprétation de scènes, à l’art numérique et au graphisme, à la fabrication, aux véhicules autonomes, à la robotique, au contrôle optimal et à la détection d’obstacles physiques. Ces secteurs exigent des modèles interprétables et fidèles aux lois de la physique pour lesquels les approches d’apprentissage profond de type « boîte noire » ne sont pas toujours adaptées. L’informatique visuelle différentiable permet d’intégrer des connaissances scientifiques dans les pipelines de données utilisées par l’apprentissage profond afin de rendre les modèles moins gourmands en données tout en étant plus aisément interprétables et contrôlables. Déjà, ces technologies ont servi à concevoir des produits dotés de propriétés optiques particulières, à contrôler des robots à corps souple, à immortaliser des étoiles du basketball en 3D, à déduire des propriétés d’objets telles que la masse et l’élasticité à partir d’une vidéo et bien d’autres choses encore.
Le pipeline de données visuelles différentiables
L’informatique visuelle permet de créer des images 2D réalistes de mondes virtuels en 3D à l’aide d’algorithmes qui simulent des phénomènes physiques tels que la propagation de la lumière et la dynamique des fluides, des corps rigides et d’autres matières. Cette conversion de mondes virtuels 3D en images ou en vidéos 2D peut être vue comme la version « directe » d’une simulation physique. Dans certaines applications, on peut aussi chercher à recueillir de l’information sur le monde 3D à partir de données 2D. On appelle ce processus complémentaire un « problème inverse ». La résolution de problèmes inverses nous permet d’appréhender et de concevoir des mondes virtuels en 3D afin de générer un résultat ou un effet particulier dans un projet de simulation physique ou un pipeline d’informatique visuelle.
Pour résoudre un problème inverse, il faut trouver l’espace des attributs de grande dimension qui caractérisent une scène 3D afin de dégager un ensemble optimal de paramètres. Ces paramètres peuvent représenter la forme géométrique d’un objet, ses propriétés optiques (couleurs, réflectivité ou translucidité), ses propriétés physiques (masse, viscosité ou élasticité) ou les propriétés du système d’imagerie utilisé (position et orientation de la caméra, profondeur de champ). En apprentissage profond, la recherche de ces paramètres se fait habituellement au moyen de la descente du gradient, un algorithme d’optimisation. Cette approche repose toutefois sur la propriété de différentiabilité par rapport à un ensemble de paramètres. C’est ainsi qu’est né le domaine de l’informatique visuelle différentiable. En concevant des pipelines d’informatique visuelle et de traitement graphique prenant en charge la différenciation, nous pouvons utiliser les mêmes méthodes d’optimisation que celles qui servent à entraîner les modèles d’apprentissage profond. De plus, avec l’informatique visuelle différentiable, les composants s’intègrent harmonieusement aux modèles d’apprentissage pour créer des systèmes hybrides alliant modèles d’apprentissage profond polyvalents et simulations fidèles aux lois de la physique.
L’un des principaux composants d’un pipeline graphique différentiable est un moteur de rendu différentiable. Tout comme les moteurs de rendu classiques, les moteurs de rendu différentiables peuvent exécuter un processus de rendu direct dans lequel une scène en trois dimensions est convertie en une image réaliste en deux dimensions. Les moteurs de rendu différentiables peuvent également rétropropager le gradient d’une image restituée vers les paramètres de la scène en trois dimensions. Cette possibilité ouvre la voie à des applications où le modèle fait l’apprentissage des paramètres de la scène 3D à partir de la supervision d’une image 2D. La première vidéo présente un exemple dans lequel le modèle assimile la lumière qui éclaire le lapin de Stanford au moyen de la descente du gradient et d’une image du lapin correspondant à la réalité du terrain. Le modèle de lapin en 3D a été obtenu auprès du Stanford 3D Scanning Repository.
La deuxième vidéo, quant à elle, présente un exemple dans lequel le modèle assimile la matière dont est fait le lapin de Stanford, toujours au moyen de la descente du gradient et d’une image du lapin correspondant à la réalité du terrain.
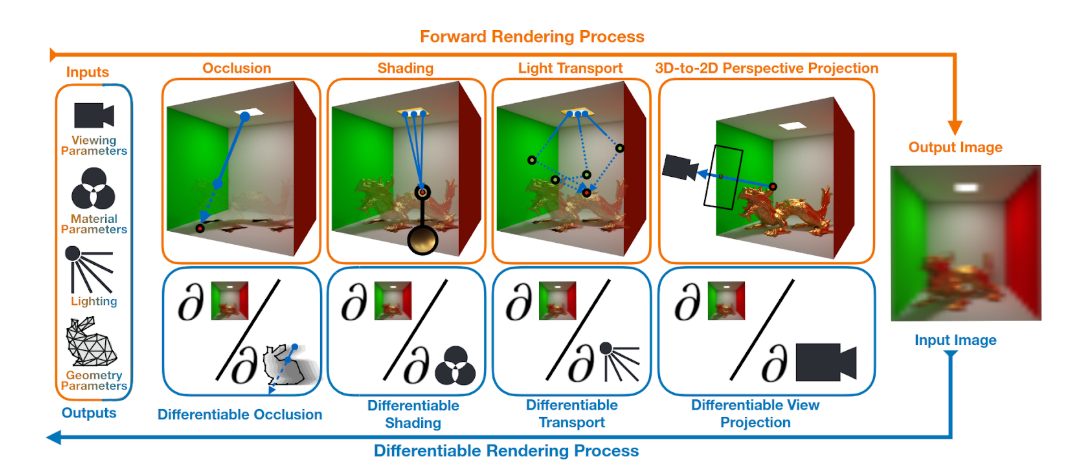


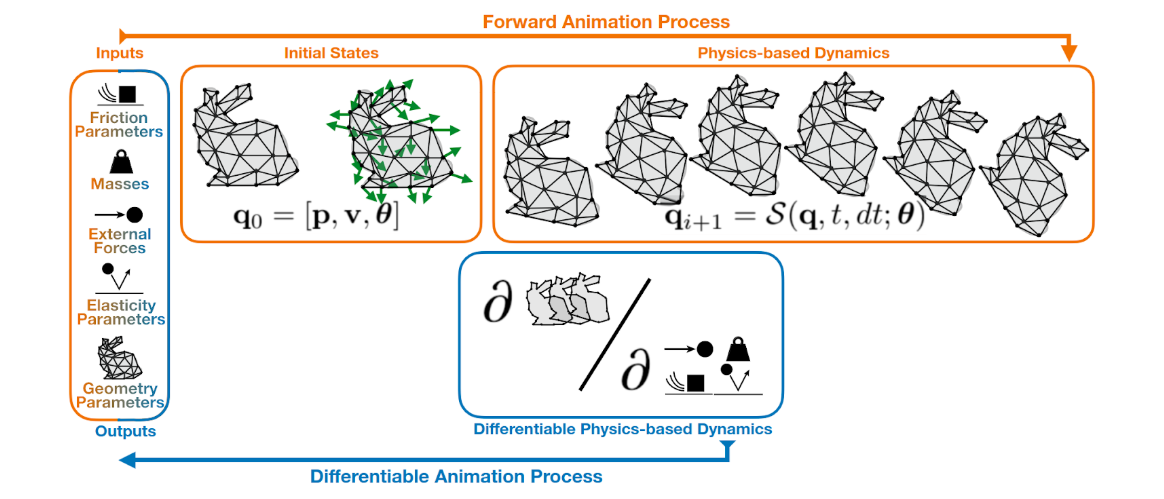
Il n’est pas rare que les pipelines d’informatique visuelle servent à créer des images de scènes dynamiques en trois dimensions. Dans ce type de scènes, les objets peuvent être animés (p. ex., le personnage peut bouger) ou leur évolution dynamique peut être reproduite au moyen de simulations des lois de la physique (p. ex., les vêtements ou les cheveux du personnage bougent au rythme de ses mouvements). On peut également rendre ces simulations différentiables et les intégrer à un pipeline d’informatique visuelle. Cette méthode convient aux applications dans lesquelles le système fait l’apprentissage, à partir de données 2D ou 3D, de paramètres physiques (p. ex., la masse de l’objet, son élasticité ou les forces externes) ou d’animations.
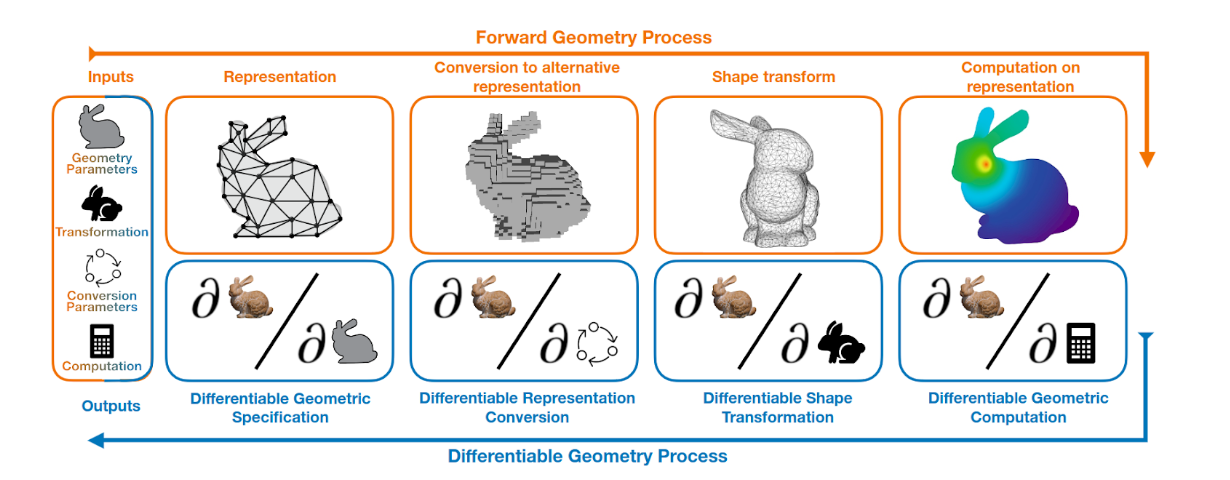
Différentes représentations géométriques d’un même objet peuvent être prises en compte à différents stades d’un pipeline d’informatique visuelle afin de donner lieu à différents processus de simulation ou de rendu. Par exemple, une représentation volumétrique peut servir à produire une simulation physique, après quoi l’objet est converti en un maillage triangulaire en vue d’être restitué. La conversion de la représentation des données ainsi que les transformations et les calculs sur les représentations sont d’autres composants essentiels des pipelines d’informatique visuelle différentiable. Ces composants font le pont entre les différents stades du pipeline tout en permettant la libre circulation du gradient d’un stade à l’autre au cours des tâches d’apprentissage.
Compléments d’information et travaux futurs
Dans un récent article de synthèse [1], Derek Nowrouzezahrai, membre académique principal de Mila et titulaire d’une chaire de recherche Ubisoft-Mila, et son équipe proposent une vision holistique et unifiée d’un pipeline d’informatique visuelle différentiable. Jordan J. Bannister, chercheur à Mila spécialisé dans l’apprentissage automatique, a récemment mis en ligne, en collaboration avec M. Nowrouzezahrai, une formation et un code source en libre accès afin d’explorer et d’expliquer les méthodes de pointe en matière de tramage des triangles [2] ainsi qu’une approche de rendu différentiable pour la création d’œuvres d’art fractales [3]. Leurs travaux actuels dans ce domaine visent à concevoir et à déployer des systèmes d’informatique visuelle différentiable afin d’appliquer l’apprentissage automatique à des contenus tridimensionnels, visuels et interactifs.
Références
[1] « Differentiable visual computing for inverse problems and machine learning ». Spielberg, A.; Zhong, F.; Rematas, K.; Jatavallabhula, K. M.; Öztireli, C.; Li, T.; Nowrouzezahrai, D. Nat. Mac. Intell., vol. 5, no 11, 2023, p. 1189-1199.
[2] « TinyDiffRast: A tiny course on differentiable triangle rasterization ». Bannister, J. J. et Nowrouzezahrai, D. https://jjbannister.github.io/tinydiffrast/. 2024
[3] « Learnable Fractal Flames ». Bannister, J. J. et Nowrouzezahrai, D., CoRR, abs/2406.09328. 2024.