Co-enseignement sensible à l’importance pour optimisation hors-ligne fondée sur un modèle

Article fondé sur une publication acceptée à NeurIPS 2023.

Problème 

Dans divers domaines, l’un des principaux objectifs est de concevoir des objets dotés de propriétés spécifiques. Par exemple, nous voulons concevoir un nouveau robot capable de courir plus vite.

Toutefois, dans le monde réel, évaluer une fonction objective peut s’avérer coûteux ou risqué. Dans ce cas, imaginons que nous devions concevoir et créer de nombreux nouveaux robots et tester leur vitesse de déplacement, afin de trouver un concept optimal, ce qui est très coûteux et prend beaucoup de temps. Par conséquent, il est souvent plus pratique de supposer que l’on a accès à un seul ensemble de données hors-ligne de concepts et à leurs scores de propriété, c.-à-d. à la paire taille de robot/vitesse de course. Ce type de problème est appelé « optimisation hors-ligne fondée sur un modèle » (OHFM). L’objectif de l’OHFM est de trouver un concept qui maximise la fonction objective inconnue en utilisant uniquement l’ensemble des données hors-ligne. Notre discussion à venir se concentrera sur cette question.

Travaux connexes et motivation

Pour résoudre le problème d’OHFM, on utilise généralement une fonction de proxy, qui est une approximation de la fonction objective inconnue. 

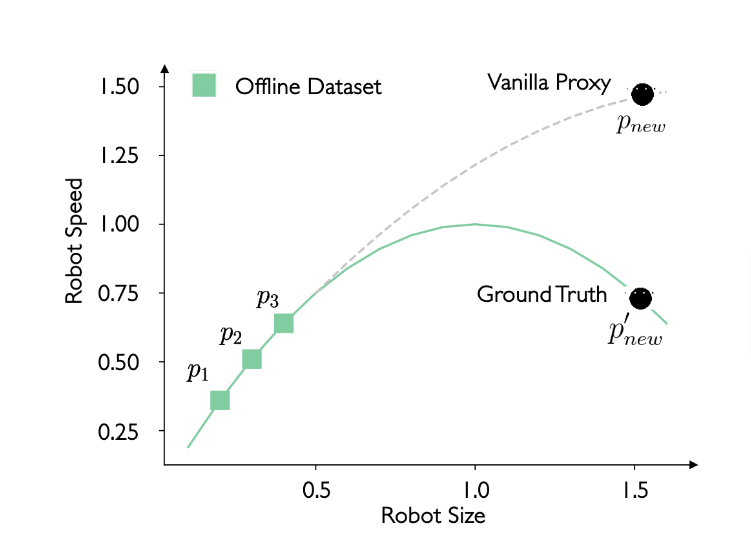
Par exemple, comme illustré ci-dessus, l’ensemble de données hors-ligne peut consister en trois paires de taille et de vitesse de robot p1, p2 et p3. Un modèle simple de réseau de neurones profond (p. ex., un perceptron multicouche à trois couches), appelé « proxy vanille », est entraîné pour cadrer avec ces trois paires, ce qui permet ensuite de prédire la vitesse de déplacement du robot en fonction de sa taille. Cependant, il peut y avoir un écart entre le « proxy vanille » et la fonction objective réelle. Dans cette étude, l’un des principaux objectifs est de réduire cet écart et de rendre notre fonction de proxy plus précise.

Co-enseignement sensible à l’importance

Nous explorons une méthode qui vise à entraîner un meilleur proxy, plus proche de la réalité, et donc à atténuer le problème de données hors-distribution.

Imaginez une meilleure situation : et si nous avions plus de points de données?

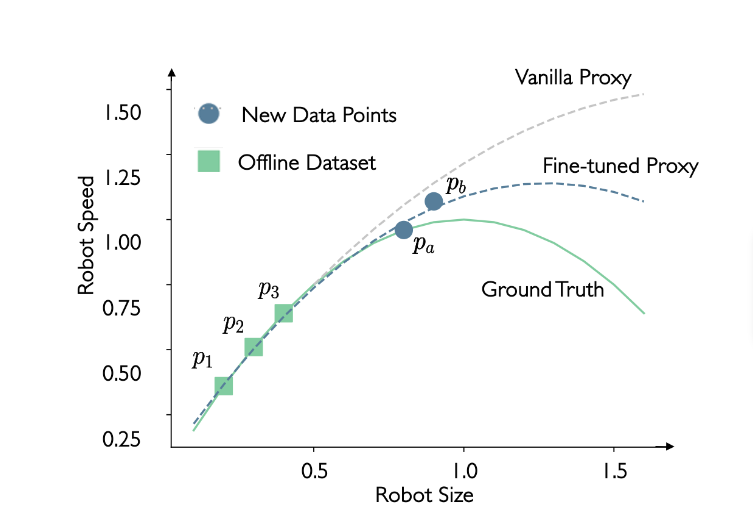
Comme le montre la figure ci-dessus, avec les nouveaux points de données pa et pb, nous pourrions être en mesure d’affiner notre proxy vanille et d’obtenir un meilleur proxy, plus proche de la fonction réelle. Toutefois, deux nouvelles questions se posent : (1) Comment obtenir ces nouveaux points de données? (2) Comment identifier les plus précis (plus proches de la fonction réelle)?

Pour relever ces deux défis, nous introduisons une nouvelle méthode : le co-enseignement sensible à l’importance (CESI, ou [Importance-aware Co-Teaching, ICT]). Cette approche permet de gérer trois proxys simultanément et se compose de deux étapes principales. 

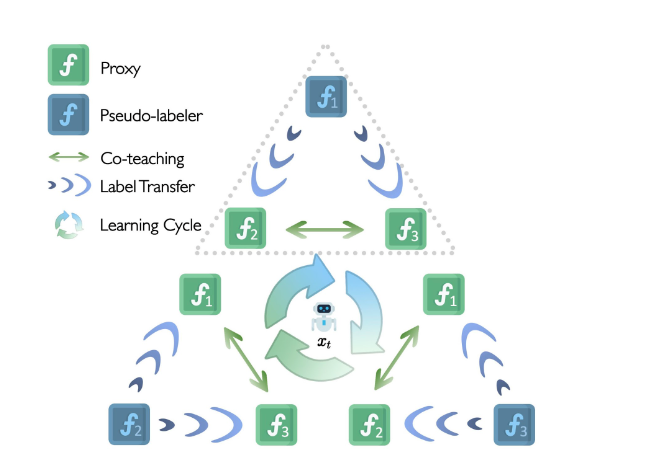
La première étape est le co-enseignement par pseudo-étiquetage. 

1. Comme illustré dans la figure ci-dessus, nous maintenons trois proxys symétriques (f1, f2 et f3) simultanément, en calculant leur ensemble moyen en tant que fonction proxy finale. 
2. Nous choisissons f1 comme pseudo-étiquetteur pour générer des pseudo-étiquettes pour un ensemble de points dans le voisinage du point d’optimisation actuel xt. Les deux autres proxys (f2 et f3) reçoivent ensuite l’ensemble de données pseudo-étiquetées. Ils calculent la valeur de perte d’échantillonage et échangent entre eux des échantillons à faible perte en vue d’un réglage fin. 
3. La nature symétrique des trois proxys permet au processus ci-dessus de se répéter trois fois, chaque proxy jouant à tour de rôle le rôle de générateur de pseudo-étiquettes.  

Ce processus de co-enseignement encourage le transfert des connaissances entre les deux proxys, car les petites pertes sont généralement révélatrices de connaissances précieuses, ce qui leur permet d’améliorer la performance de l’ensemble dans le traitement des concepts de données hors-distribution.

Par ailleurs, nous introduisons la repondération des échantillons fondée sur le méta-apprentissage comme deuxième étape de l’approche CESI, qui vise à attribuer des pondérations plus élevées aux points les plus précis et des pondérations plus faibles aux points les moins précis dans l’ensemble de données pseudo-étiquetées. Pour ce faire, il faut procéder comme suit :

1. Nous attribuons une pondération d’importance à chaque échantillon obtenu lors de la première étape.
2. Pour actualiser ces pondérations d’importance, nous nous appuyons sur les signaux de supervision de l’ensemble de données hors-ligne. Si les pondérations des échantillons sont exactes, le proxy affiné sur les échantillons pondérés devrait donner de bons résultats sur l’ensemble de données hors-ligne. 
3. Lors de la mise à jour des pondérations d’importance, nous fixons le modèle et calculons les gradients par rapport aux pondérations d’importance, puis nous utilisons la descente de gradient pour mettre à jour celles-ci.

Résultats expérimentaux

Dans cette étude, nous menons des expériences sur quatre tâches continues et trois tâches discrètes. Les tâches continues comprennent ce qui suit :

(a) Supraconducteur (SupraC), dont l’objectif est de mettre au point un supraconducteur composé de plusieurs éléments continus afin de maximiser la température critique; 

(b) Morphologie de type Fourmi (Fourmi) et morphologie de type D’Kitty (D’Kitty), dont l’objectif est de concevoir une Fourmi ou un D’Kitty quadrupède ayant des composants continus afin d’améliorer la vitesse de rampement; 

(c) Hopper Controller (Hopper), dont l’objectif est d’identifier une politique de réseau de neurones avec des milliers de pondérations afin d’optimiser le rendement. 

En outre, nos tâches discrètes comprennent les suivantes :

(d) TF Bind 8 (TF8) et TF Bind 10 (TF10), dont l’objectif est de découvrir une séquence d’ADN de 8 unités ou de 10 unités qui maximise le résultat d’activité de liaison; 

(e) NAS, dont l’objectif est de trouver l’architecture optimale de réseau de neurones pour améliorer la précision des tests sur l’ensemble de données CIFAR-10.

En résumé, nous visons à déterminer les concepts ou les séquences optimaux pour chaque tâche, en ciblant le potentiel maximal du sujet, qu’il s’agisse d’un robot, d’une séquence d’ADN ou d’un supraconducteur. Pour évaluer la performance de notre méthode, nous indiquons le score normalisé du concept le plus performant pour chaque tâche. Ce score offre un moyen uniforme d’évaluer la performance de chaque modèle par rapport à celle de ses pairs, garantissant ainsi une mesure directe permettant d’effectuer une comparaison juste.

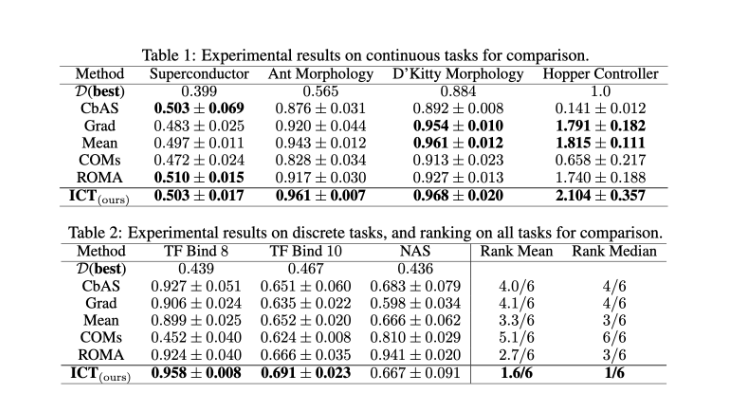
D’après nos résultats expérimentaux, nous observons les points clés suivants :

1. Dans les quatre tâches continues, notre méthode CESI obtient la meilleure performance. En particulier, elle surpasse l’ascension de gradient de base (Grad), ce qui démontre sa capacité à atténuer le problème de données hors distribution.
2. De plus, l’approche CESI surpasse généralement les méthodes d’ensemble moyennes (Mean) et d’autres techniques fondées sur le gradient, comme COM et ROMA, ce qui démontre l’efficacité de notre stratégie.
3. Les méthodes fondées sur un modèle génératif, comme CbAS, se heurtent toutefois à la tâche hautement dimensionnelle qu’est Hopper Controller. Il est intéressant de noter que l’approche CESI ne nécessite que trois proxys standards et évite d’avoir à entraîner un modèle génératif, ce qui peut souvent s’avérer une tâche difficile.
4. La méthode CESI atteint les meilleures performances dans deux des trois tâches discrètes, à savoir TF Bind 8 et TF Bind 10.
5. Elle obtient les meilleurs classements avec une moyenne de 1,6/6 et une médiane de 1/6 parmi de nombreuses méthodes de référence, comme le montrent les tableaux ci-dessus. Elle obtient également les meilleures performances dans 6 des 7 tâches. Ces résultats indiquent que l’approche CESI constitue une base de référence simple mais puissante pour l’optimisation hors ligne fondée sur un modèle.

Conclusion

Nous présentons l’approche CESI, une solution au problème de données hors-distribution omniprésent dans l’optimisation hors-ligne fondée sur un modèle. Cette méthode démontre l’efficacité du transfert des connaissances entre les trois proxys et améliore la performance de l’ensemble en conséquence, ce qui peut atténuer le problème de données hors-distribution dans le cadre de l’optimisation fondée sur un modèle. Nos résultats expérimentaux démontrent le succès de l’approche CESI.