Retour à tous les articles 
Les réseaux de flot génératifs (RFG) ou GFlowNets sont de nouveaux algorithmes d’apprentissage automatique qui permettent d’apprendre à échantillonner des distributions sur des objets compositionnels. Ces distributions, souvent complexes (par exemple, elles peuvent avoir de nombreux pics ou modes), sont donc difficiles à échantillonner. Les réseaux de flot génératifs relèvent ce défi en tirant parti des avancées de l’apprentissage profond et ont été utilisés avec succès pour la découverte de médicaments, la modélisation de graphes causaux et dans d’autres domaines. En modélisant la distribution complète des solutions plausibles, ces nouveaux algorithmes peuvent conduire à des systèmes d’intelligence artificielle plus performants et ainsi faciliter la conception de scénarios complexes, accélérer la découverte scientifique et raisonner de manière robuste, comme le font les humains.
Pour un tutoriel sur les RFG, consultez le tutoriel.
Les RFG sont étroitement liés à de nombreux domaines de recherche en IA, notamment l’apprentissage par renforcement et l’inférence variationnelle (IV). L’apprentissage par renforcement modélise le comportement des agents qui cherchent à optimiser la récompense attendue en interagissant avec l’environnement. L’IV transforme le problème de l’inférence en un problème d’approximation de distributions de probabilités difficiles à calculer alors que les RFG résolvent un problème d’IV en utilisant des méthodes d’apprentissage par renforcement. Prenons l’exemple de la découverte de médicaments. Nous disposons d’un modèle de récompense qui juge de l’intérêt d’une molécule donnée pour un médicament. Il est tentant de demander la molécule qui optimise la récompense, mais comme le modèle n’est qu’une approximation de la valeur du médicament, nous voulons avoir plusieurs candidats pour les tester dans le monde réel. Par conséquent, nous aimerions échantillonner approximativement les molécules proportionnellement à leur intérêt selon le modèle, ce qui est un problème d’IV. À l’instar de l’apprentissage par renforcement, un RFG décompose la production d’une molécule en une succession d’actions simples, comme l’ajout d’un atome. En réduisant les objectifs du RFG à zéro, nous obtiendrons un tel échantillonneur à la fin de l’entraînement.
Notre travail vise à expliciter les liens entre les réseaux de flot génératifs et l’inférence variationnelle.
Les méthodes variationnelles, qui étaient à l’origine un outil de physique mathématique, ont donné naissance à plusieurs des idées les plus importantes en matière d’apprentissage automatique au cours des dernières décennies, notamment les algorithmes Wake-Sleep et les auto-encodeurs variationnels. L’idée qui sous-tend les IV peut être décrite comme une « inférence par optimisation ». Imaginons une distribution difficile à échantillonner. Au lieu de l’échantillonner directement, nous nous demandons : « Quelle distribution simple, que nous sommes en mesure d’échantillonner, se rapproche de la vraie distribution? » La distribution simple que nous choisissons a souvent des paramètres entraînables, tels que la moyenne et la covariance d’une distribution gaussienne. En optimisant ces paramètres, nous sommes en mesure de nous rapprocher de la vraie distribution tout en réalisant l’échantillonnage avec une relative facilité.
À première vue, les RFG et l’IV servent à résoudre des problèmes différents. Par exemple, l’IV est généralement appliquée à des variables aléatoires continues, alors que les RFG modélisent des structures discrètes complexes construites en plusieurs étapes. Certains algorithmes d’IV, tels que les algorithmes hiérarchiques et imbriqués, sont applicables à ce contexte, où la distribution cible est approximée par l’échantillonnage d’une séquence de quantités aléatoires, une à la fois, chaque choix dépendant des précédents. Toutefois, ces algorithmes utilisent des objectifs d’optimisation différents : l’IV réduit les mesures de divergence entre les distributions échantillonnées et les distributions cibles, tandis que les RFG optimisent des objectifs tels que la correspondance des flots et l’équilibre des trajectoires, qui non seulement s’adaptent à la distribution cible, mais optimisent également les mesures de cohérence interne. Dans notre article, intitulé GFlowNets and Variational Inference, nous présentons une vue d’ensemble de ces deux cadres et étudions leurs compromis respectifs.
En bref, les RFG ayant un objectif d’équilibre des trajectoires sont étroitement liés à l’IV hiérarchique. Cependant, l’objectif de l’IV hiérarchique tend à modéliser uniquement la meilleure solution (en utilisant la divergence inverse de Kullback-Leibler) ou une combinaison de plusieurs solutions (en utilisant la divergence directe de K-L). Les objectifs des RFG offrent un meilleur compromis entre les deux et permettent de trouver davantage de modes de haute qualité. En outre, les objectifs des RFG produisent un gradient plus stable, et leur puissance peut être augmentée avec un apprentissage hors politique. Une politique est un modèle de prise de décision qui indique ce qu’il faut faire dans une situation donnée. Par exemple, étant donné une molécule partiellement construite, une politique indique quel atome ajouter pour construire un bon candidat pour un médicament. L’apprentissage hors politique améliore une politique en suivant une politique différente, potentiellement plus exploratoire, ce qui permet d’appréhender diverses solutions dans le cadre de la fonction de récompense. Imaginez que nous connaissions quelques façons de construire de bonnes molécules médicamenteuses. Si nous nous en tenons à ce que nous savons, c’est-à-dire si nous respectons toujours la même politique, nous n’aurons jamais l’occasion d’explorer des combinaisons d’atomes plus efficaces que celles que nous connaissons déjà. L’apprentissage hors politique nous permet de tenter notre chance et d’apprendre potentiellement quelque chose de nouveau. Nos expériences montrent que les RFG sont beaucoup plus faciles à entraîner hors politique que les IV hiérarchiques. Cela est dû au fait que les objectifs des RFG ne nécessitent pas d’échantillonnage important, contrairement aux IV hiérarchiques.
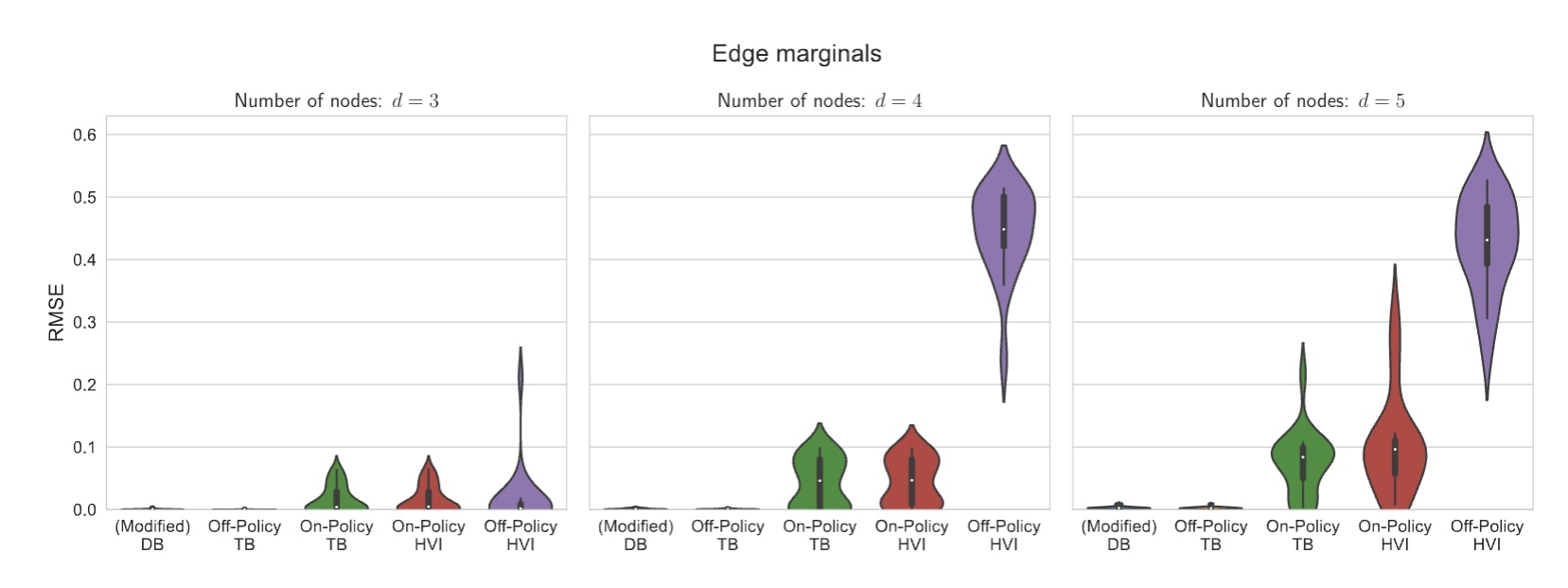
Dans l’une de nos expériences empiriques, nous étudions dans quelle mesure les RFG et les IV hiérarchiques peuvent modéliser une distribution sur des graphes causaux à partir de données d’observation. Les graphes causaux modélisent les relations de causalité entre les variables d’intérêt. Par exemple, la consommation de crème glacée et la température sont toutes deux en corrélation avec une plage bondée. Cependant, une seule de ces relations est causale. En général, en raison du manque de données d’intervention, de nombreux graphes causaux pourraient correspondre aux données, alors qu’il n’existe qu’un seul véritable modèle. En raison de cette ambiguïté, il est important de saisir tous les modes probables au lieu de s’en tenir à un seul.
Lorsqu’il existe plusieurs bonnes solutions ou modes, nous nommons la distribution correspondante sur les solutions comme étant multimodale. La distribution sur les graphes dans l’exemple ci-dessus est multimodale parce que de nombreux graphes sont également capables d’expliquer les observations. En outre, cette distribution particulière présente une complexité qui croît de manière exponentielle avec la taille du graphe. Par conséquent, nous voyons un avantage important à utiliser les RFG même sur les petits graphes. Sur des graphes ne comportant que trois nœuds, la performance moyenne, mesurée par la racine de l’erreur quadratique moyenne (plus elle est faible, mieux c’est), est presque identique pour les RFG et les IV hiérarchiques. Toutefois, lorsque la taille des graphes passe à quatre ou cinq nœuds, l’apprentissage hors politique devient nécessaire, et les RFG surpassent largement les IV hiérarchiques.
Légende : Nous validons la capacité de différents algorithmes à modéliser une distribution sur des graphes causaux en utilisant la racine de l’erreur quadratique moyenne (RMSE en anglais) entre la distribution estimée et la distribution réelle sur les graphes orientés acycliques. Une RMSE moins élevée est préférable. DB et TB font référence aux différentes pertes des RFG utilisées lors de l’apprentissage. Les RFG avec apprentissage hors politique peuvent gérer des graphes plus grands, ce qui n’est pas le cas de l’IV hiérarchique. Consultez notre article pour plus de détails.
Nous espérons que les travaux futurs permettront de découvrir de meilleures méthodes d’entraînement des réseaux de flot génératifs fondées sur la littérature existante sur les inférences variationnelles hiérarchiques, et vice versa. Pour plus de détails, veuillez consulter notre article GFlowNets and Variational Inference sur arXiv.
