Note de la rédaction : Ce billet a été publié à l’origine sur le Google AI Blog le 17 novembre 2021 et est basé sur ce texte qui a reçu le prix du meilleur article à NeurIPS en 2021. Ce travail a été réalisé en collaboration avec Max Schwarzer, Aaron Courville et Marc G. Bellemare de Mila.
L’apprentissage par renforcement est un volet de l’apprentissage automatique qui se concentre sur l’apprentissage à partir d’expériences pour accomplir des tâches de prise de décision. Le domaine de l’apprentissage par renforcement a considérablement progressé et a obtenu des résultats empiriques impressionnants dans le cadre de tâches complexes, comme jouer à des jeux vidéo, faire voler des ballons stratosphériques et concevoir des puces électroniques. Pourtant, il devient de plus en plus évident que les normes actuelles d’évaluation empirique peuvent donner la fausse impression que les progrès scientifiques sont rapides alors qu’elles les ralentissent.
À cette fin, nous présentons ici « Deep RL at the Edge of the Statistical Precipice » qui a obtenu le prix du meilleur article à NeurIPS 2021. Nous discutons de la façon dont l’incertitude statistique des résultats doit être prise en compte, en particulier lorsqu’on n’utilise que quelques séquences d’entraînement, afin d’assurer une évaluation fiable en apprentissage par renforcement profond. Plus précisément, la pratique prédominante consistant à rapporter les estimations ponctuelles fait abstraction de cette incertitude et nuit à la reproductibilité des résultats. De même, les tableaux contenant les scores par tâche, comme ceux qui sont couramment présentés, peuvent être saturés après quelques tâches et omettent souvent les écarts types. De plus, des mesures de performance simples comme la moyenne peuvent être dominées par quelques tâches marginales, tandis que le score médian ne serait pas affecté même si la moitié des tâches obtenait des scores de performance de zéro. Ainsi, afin d’accroître la confiance du milieu dans les résultats rapportés à partir d’un petit nombre de séquences, nous proposons divers outils statistiques, notamment des intervalles de confiance bootstrap stratifiés, des profils de performance ainsi que des mesures plus adéquates, comme la moyenne interquartile et la probabilité d’amélioration. Pour aider les chercheurs à intégrer ces outils, nous avons également publié une bibliothèque Python facile d’utilisation, RLiable, ainsi qu’un guide collaboratif de démarrage.
L’incertitude statistique dans l’évaluation de l’apprentissage par renforcement
La recherche empirique en apprentissage par renforcement s’appuie sur l’évaluation des performances pour une série de tâches diverses, comme avec les jeux vidéo Atari 2600, pour évaluer les progrès. Les résultats publiés des tests de référence de l’apprentissage par renforcement profond comparent généralement les estimations ponctuelles des scores moyens et médians agrégés pour l’ensemble des tâches. Ces scores sont généralement relatifs à une base de référence définie et à une performance optimale (par exemple, la performance d’un agent aléatoire et la performance humaine « moyenne » sur les jeux Atari, respectivement) afin de rendre les scores comparables entre les différentes tâches.
Dans la plupart des expériences en apprentissage par renforcement, les scores obtenus à partir de différentes séquences d’entraînement présentent un caractère aléatoire, de sorte que le fait de ne présenter que des estimations ponctuelles ne permet pas de savoir si des résultats semblables seraient obtenus avec de nouvelles séquences indépendantes. Un petit nombre de séquences d’entraînement, associé à la grande variabilité des performances des algorithmes d’apprentissage par renforcement profond, entraîne souvent une grande incertitude statistique dans ces estimations ponctuelles.
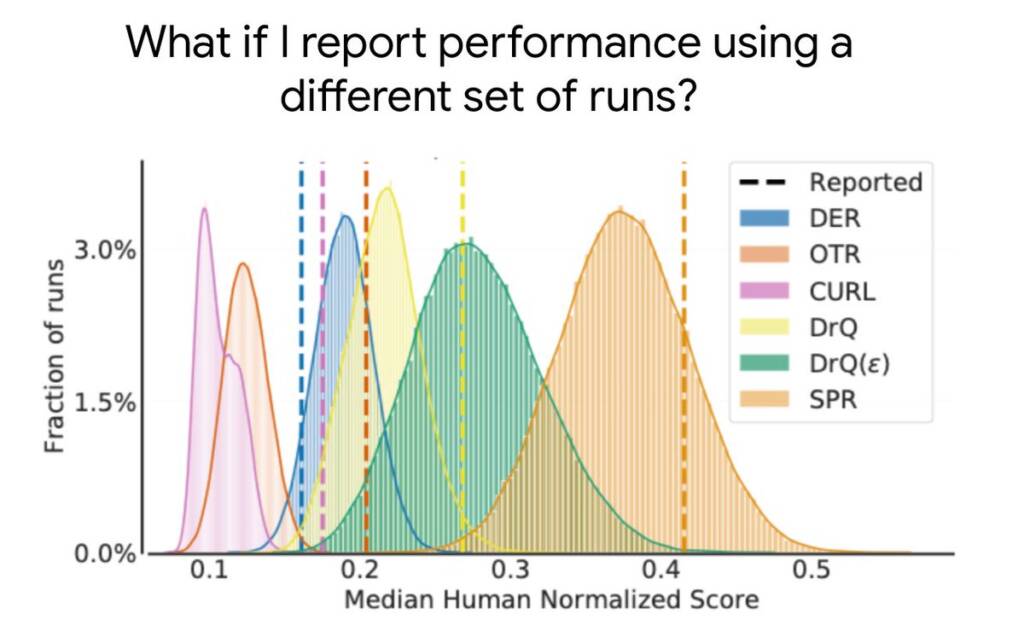
Comme les tests de performance deviennent de plus en plus complexes, l’évaluation de plus de quelques séquences sera de plus en plus exigeante en raison de l’augmentation des calculs et des données nécessaires à la résolution de telles tâches. Par exemple, 5 séquences sur 50 jeux Atari pour 200 millions d’images nécessitent plus de 1000 jours GPU. Ainsi, l’évaluation d’un plus grand nombre de séquences n’est pas une solution envisageable pour réduire l’incertitude statistique de méthodes exigeantes en matière de calcul. Bien que des travaux antérieurs aient recommandé des tests de signification statistique comme solution, ces tests sont dichotomiques par nature (résultats « significatifs » ou « non significatifs »), de sorte qu’ils manquent souvent de la granularité nécessaire pour donner des informations pertinentes et sont souvent mal interprétés.
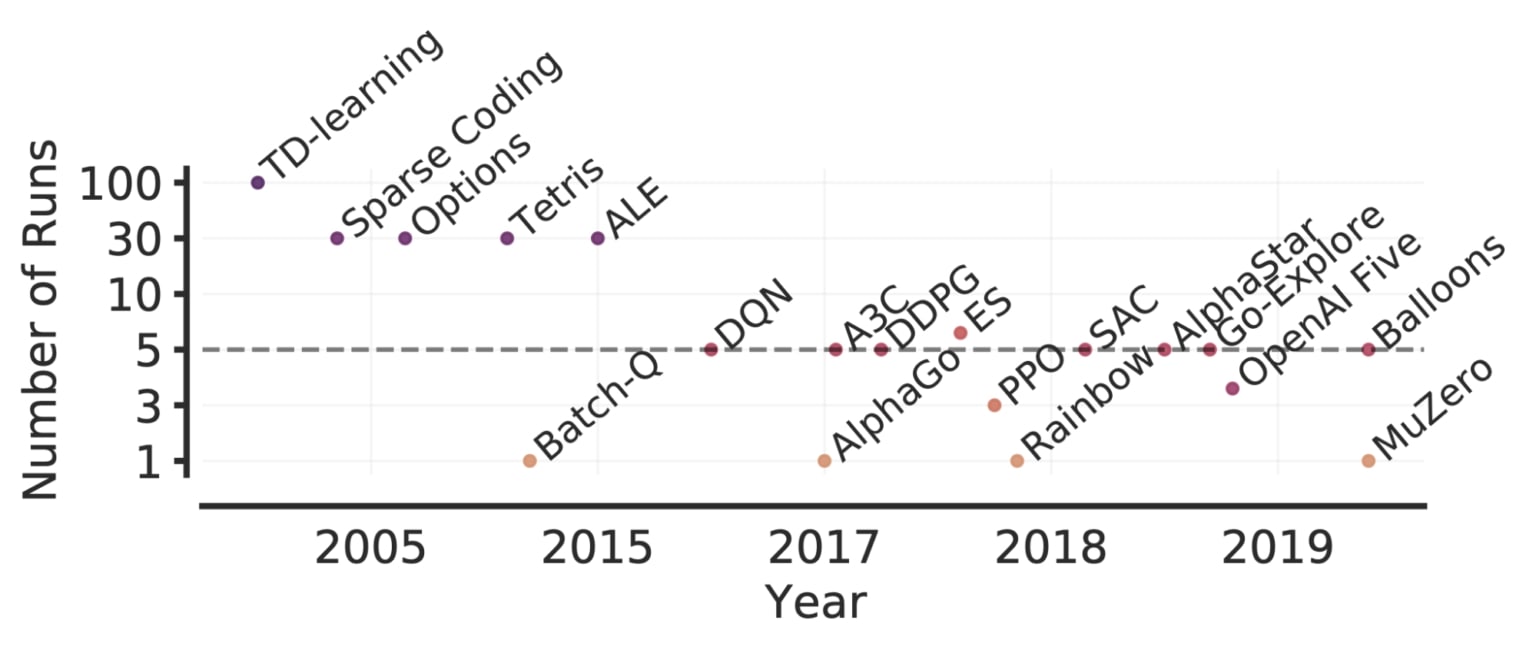
Outils pour une évaluation fiable
Toute métrique agrégée basée sur un nombre fini de séquences est une variable aléatoire. Pour en tenir compte, nous préconisons de rapporter des intervalles de confiance bootstrap stratifiés qui prédisent les valeurs probables des métriques agrégées si la même expérience était répétée avec différentes séquences. Ces intervalles de confiance nous permettent de comprendre l’incertitude statistique et la reproductibilité des résultats. Ils utilisent les scores de séquences combinées pour l’ensemble des tâches. Par exemple, en évaluant 3 séquences sur Atari 100k, qui contient 26 tâches, on obtient 78 scores d’échantillon pour l’estimation de l’incertitude.
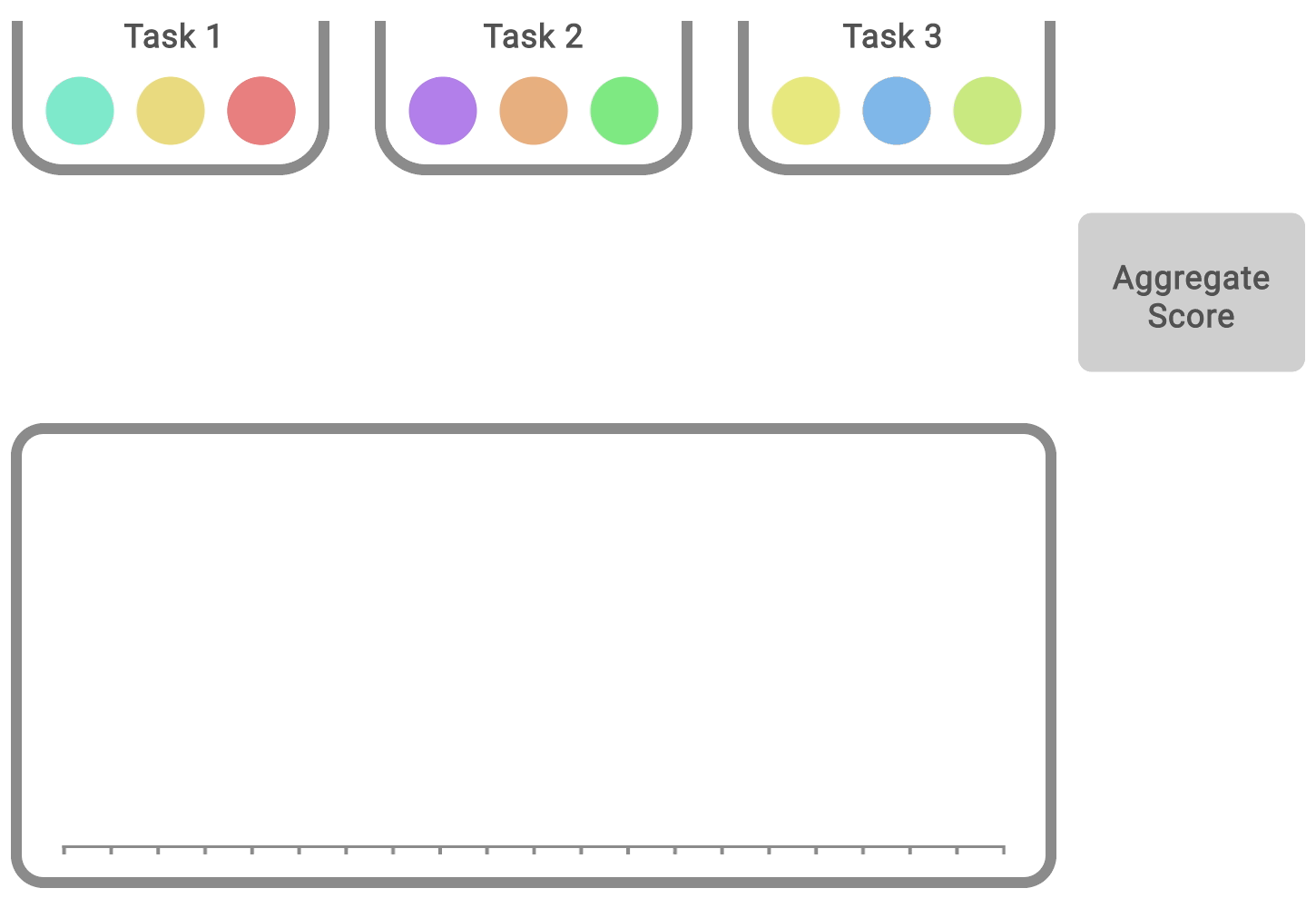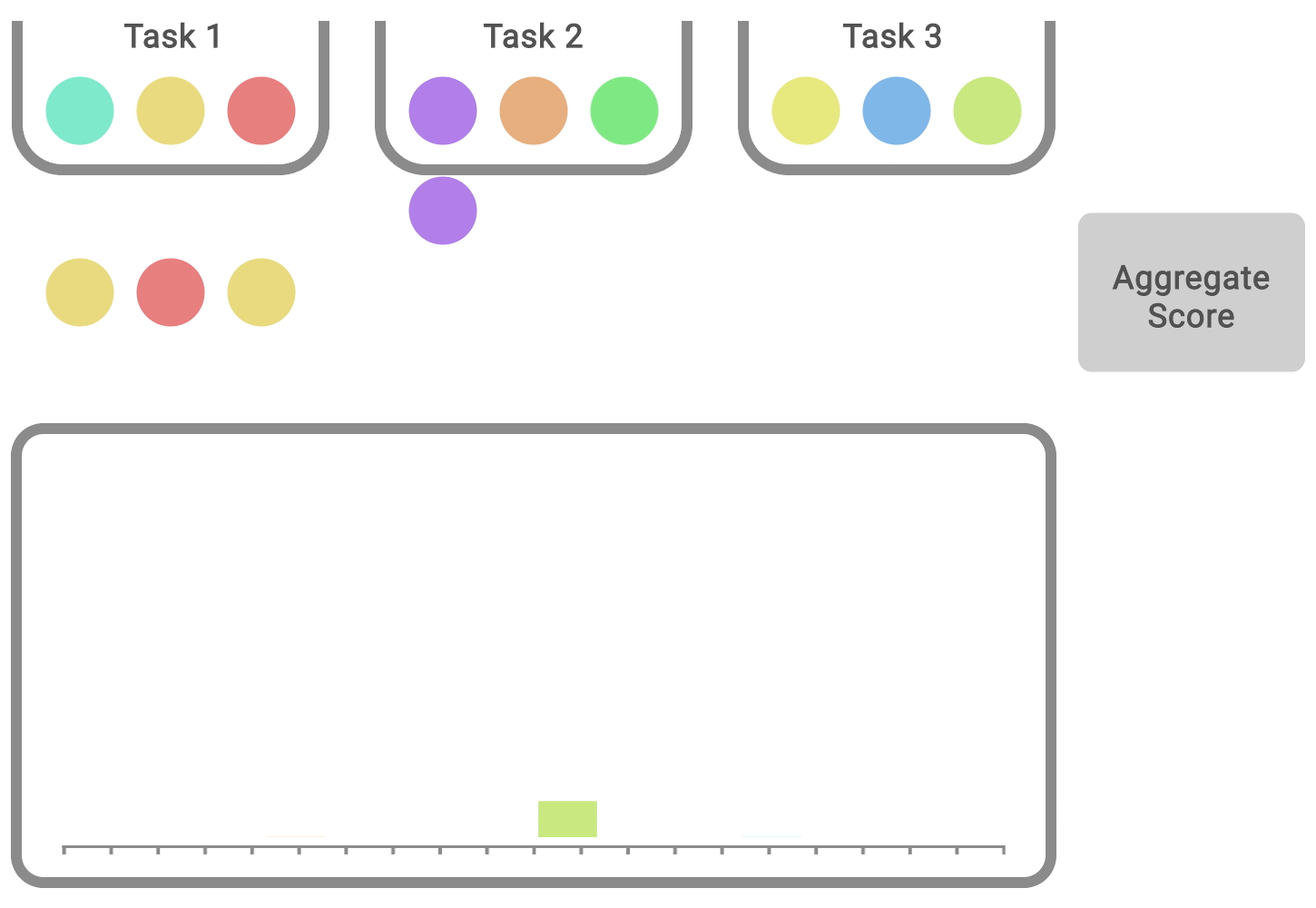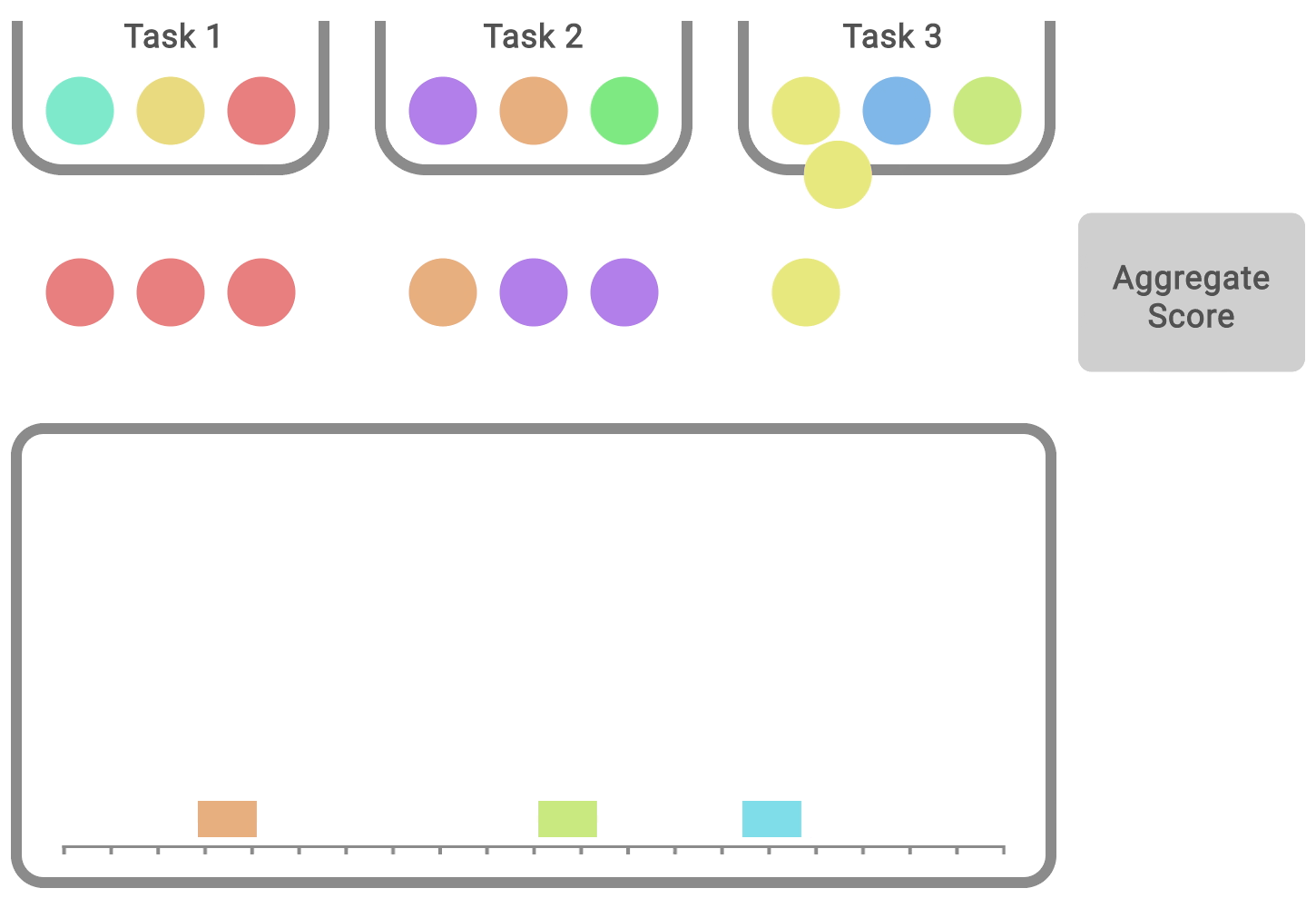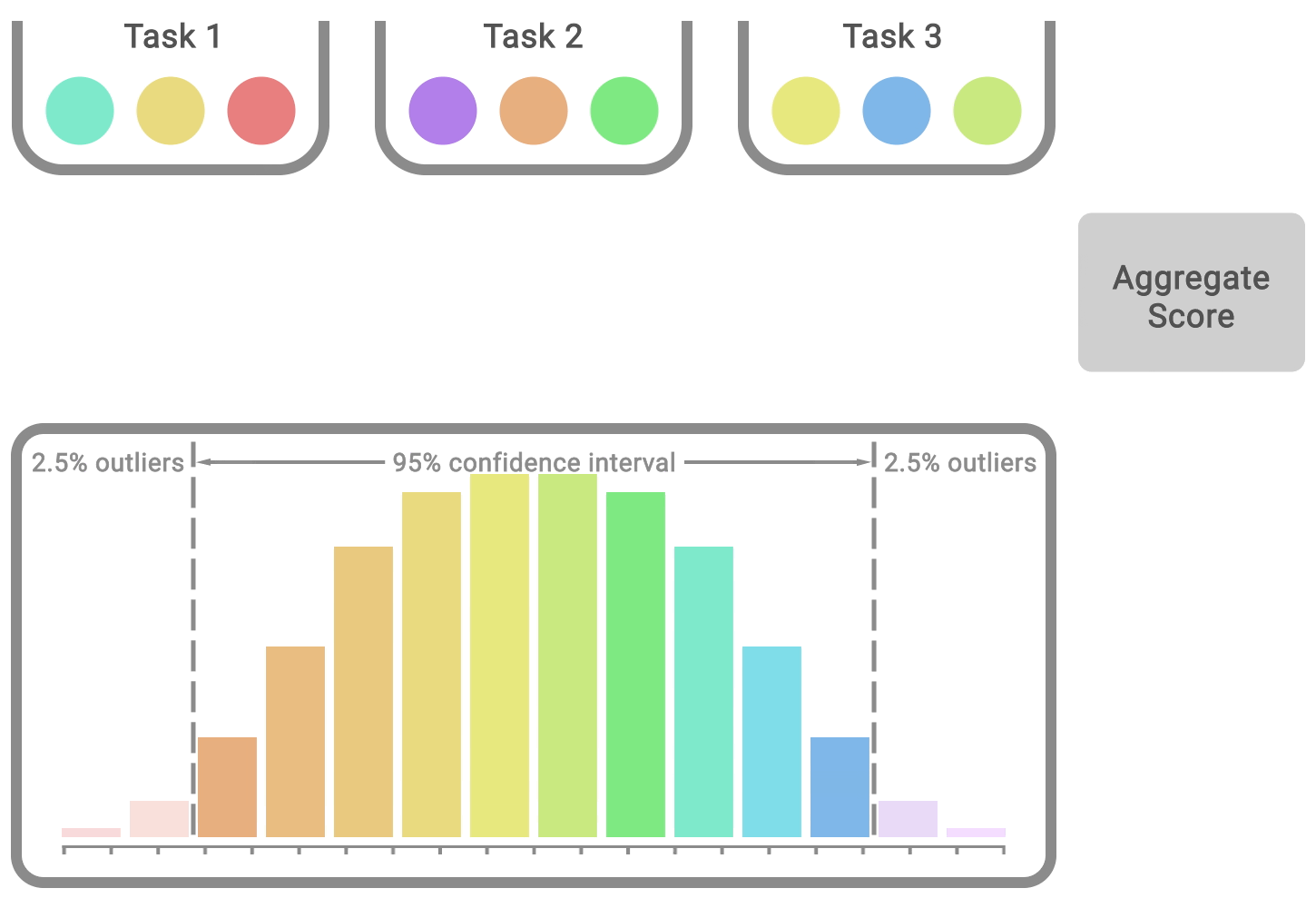
La plupart des algorithmes en apprentissage par renforcement profond sont souvent plus performants pour certaines tâches et certaines séquences d’entraînement, mais les mesures de performance agrégées peuvent dissimuler cette variabilité, comme le montre le graphique ci-dessous.
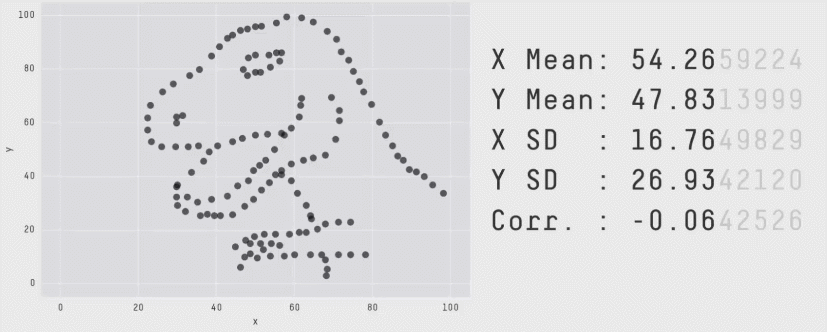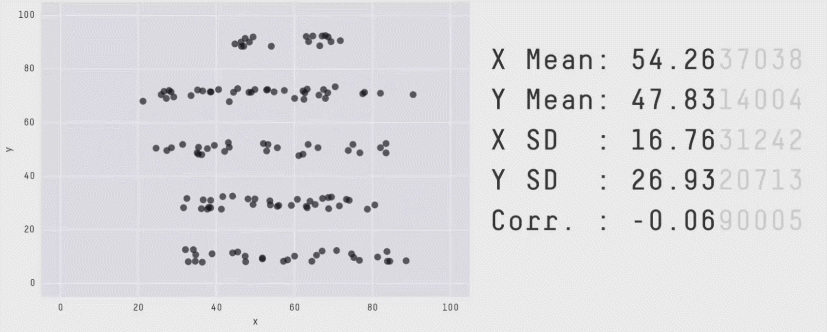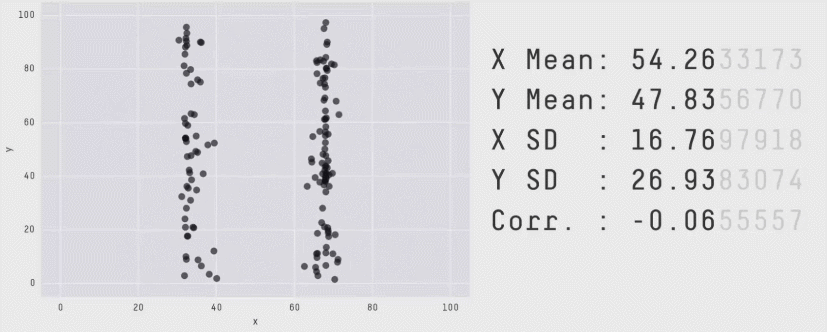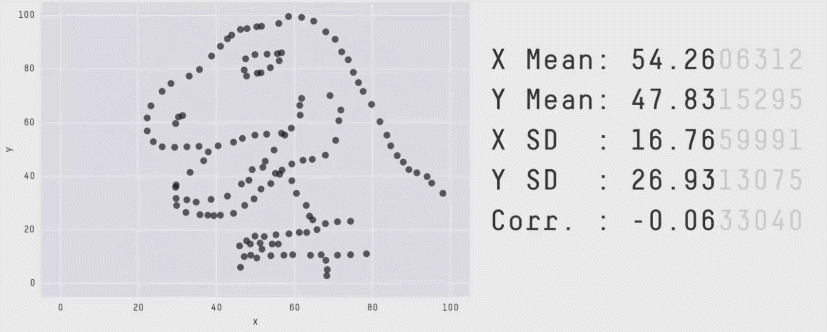
Nous recommandons plutôt les profils de performance, qui sont généralement utilisés pour comparer les temps de résolution des logiciels d’optimisation. Ces profils présentent la distribution des scores sur l’ensemble des séquences et des tâches avec des estimations d’incertitude utilisant des zones de confiance bootstrap stratifiées. Ces graphiques montrent le nombre total de séquences dans toutes les tâches qui obtiennent un score supérieur à un seuil (𝝉) comme fonction du seuil.
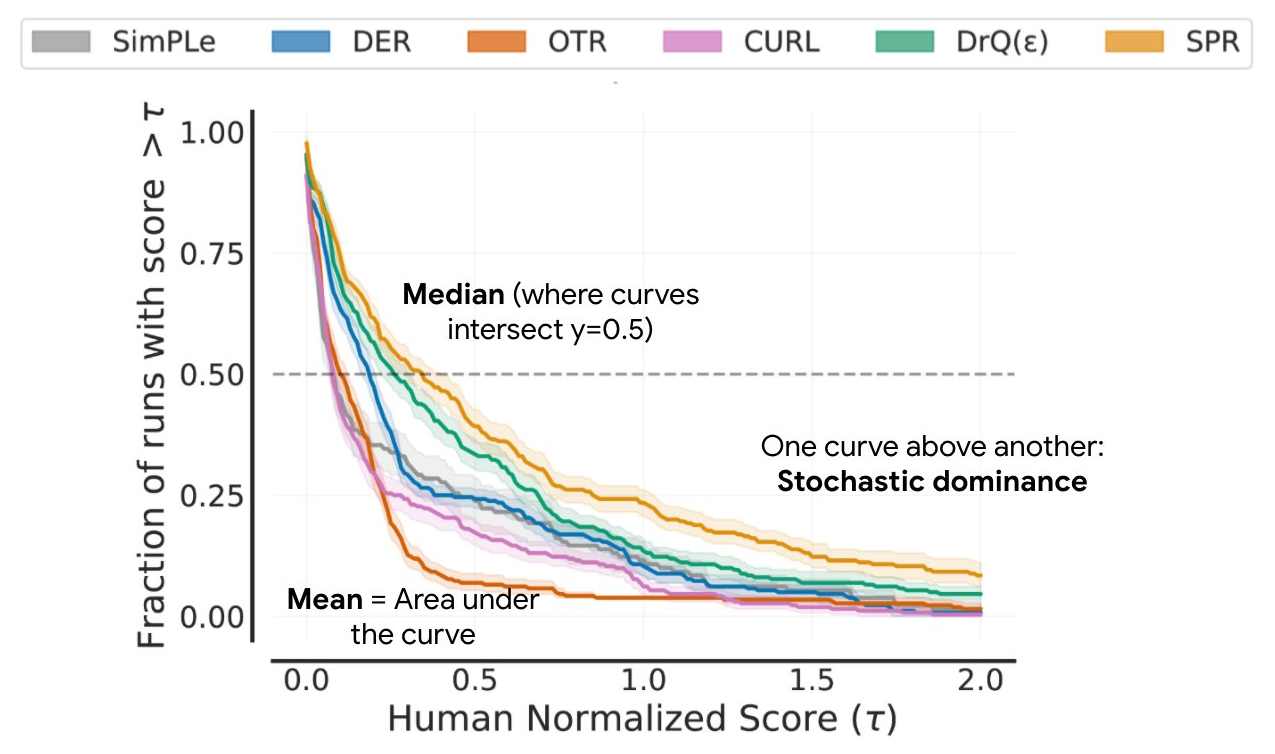
Ces profils permettent de faire des comparaisons qualitatives en un coup d’œil. Par exemple, lorsque la courbe d’un algorithme se situe au-dessus d’une autre, cela signifie que l’algorithme est meilleur que l’autre. Nous pouvons également lire le percentile de n’importe quel score : par exemple, les profils croisent y = 0,5 (ligne pointillée ci-dessus) pour le score médian. En outre, la zone sous le profil correspond au score moyen.
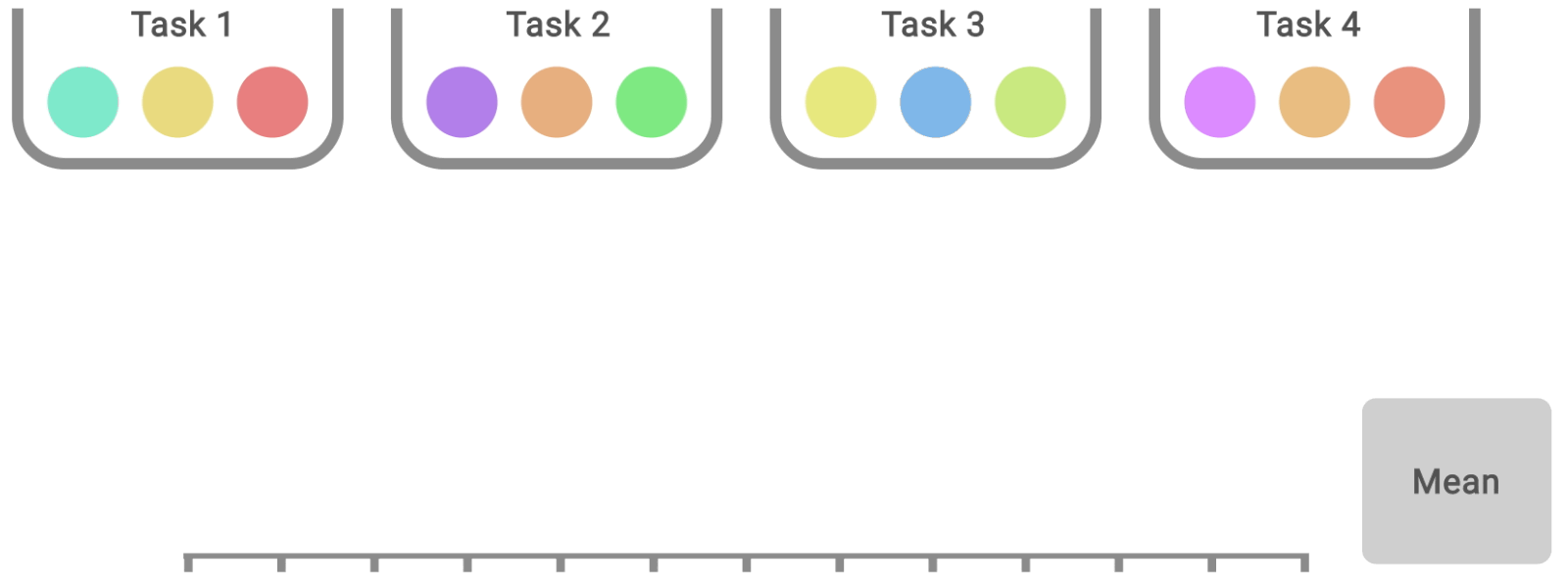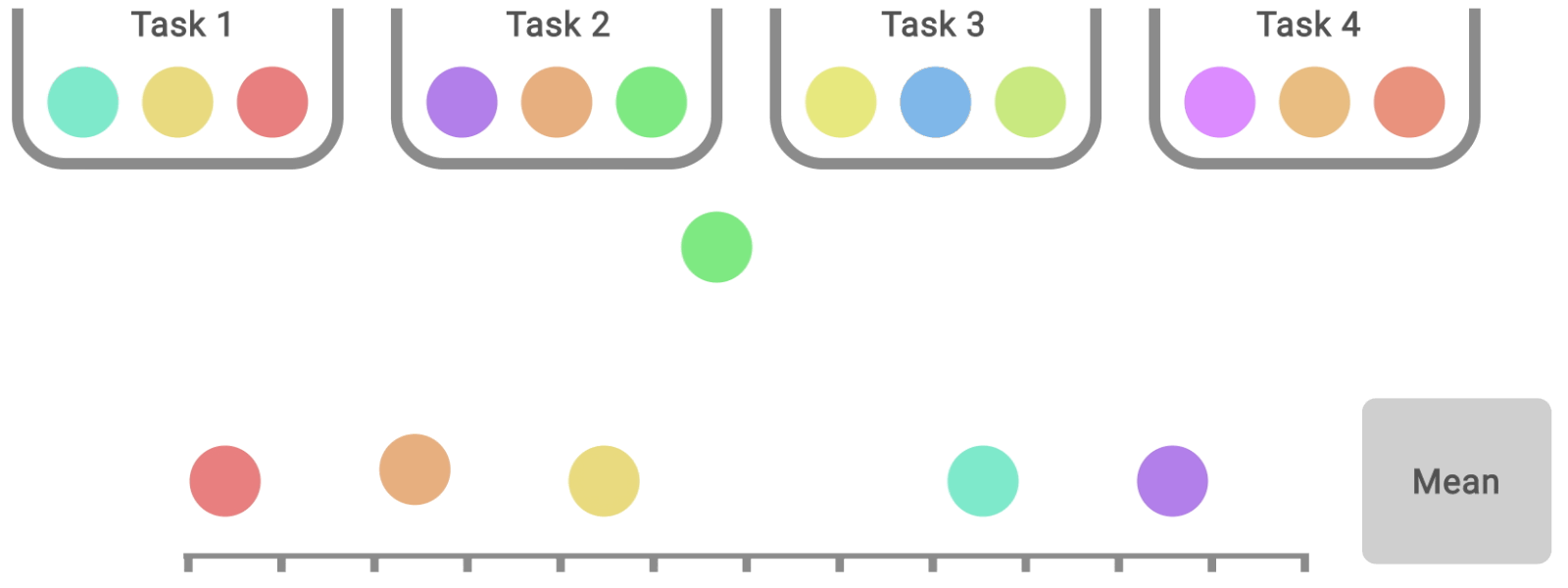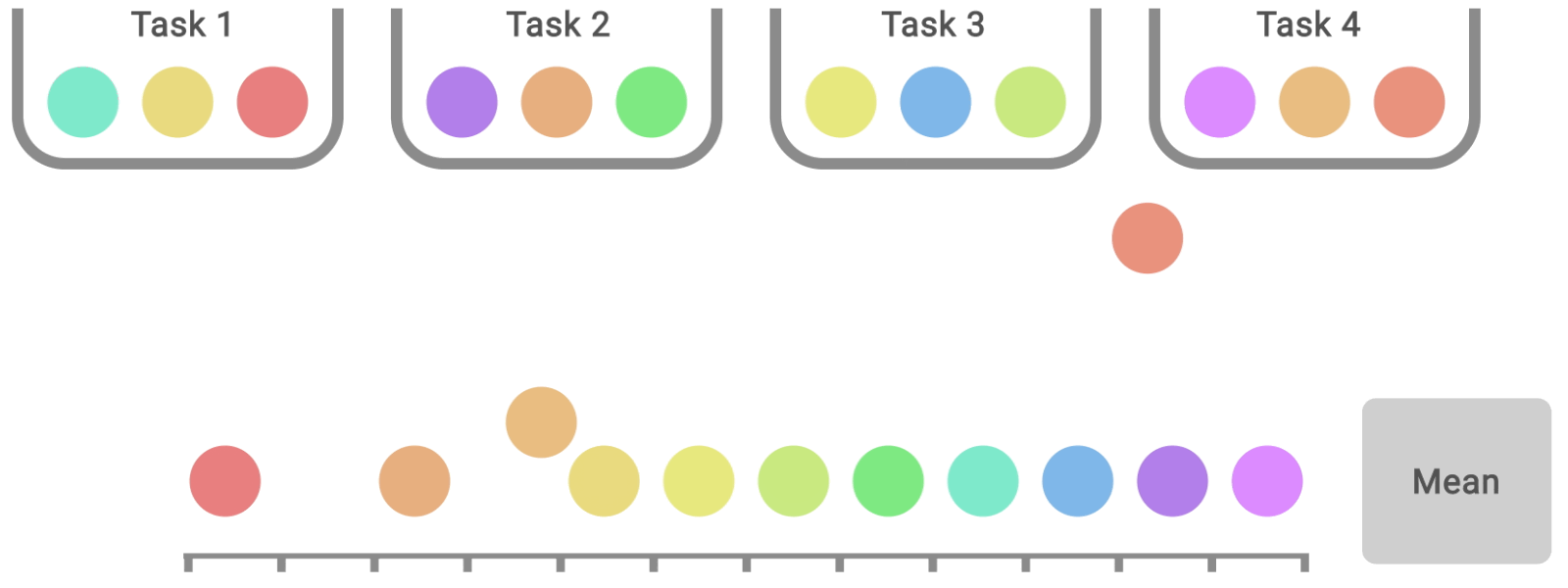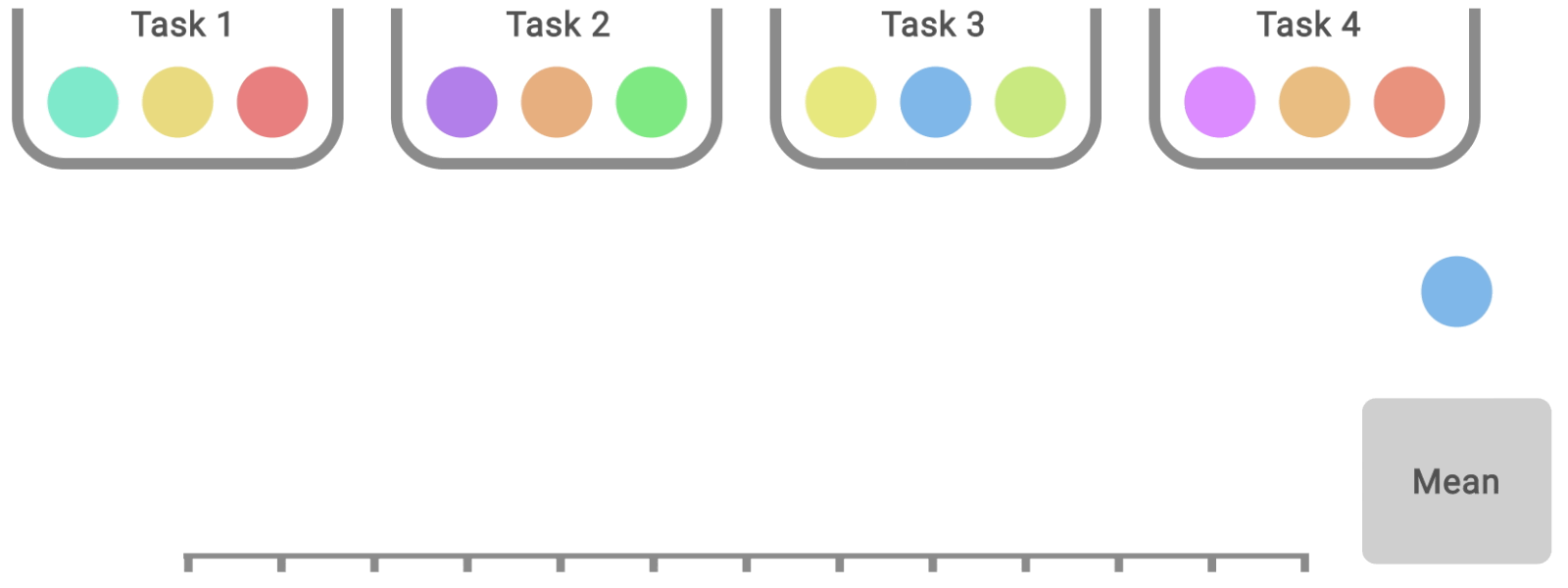
Si les profils de performance sont utiles pour les comparaisons qualitatives, il faut souligner qu’un algorithme est rarement plus performant que les autres algorithmes pour toutes les tâches. Par conséquent, leurs profils se croisent souvent, et les comparaisons quantitatives plus fines nécessitent des mesures de performance agrégées. Cependant, les métriques existantes présentent des limites : (1) une seule tâche très performante peut dominer le score moyen de la tâche, tandis que (2) le score médian de la tâche n’est pas affecté par des scores nuls pour près de la moitié des tâches et nécessite un grand nombre de séquences d’entraînement pour obtenir une faible incertitude statistique. Pour remédier à ces limitations, nous recommandons deux solutions basées sur la robustesse statistique: la moyenne interquartile et l’écart d’optimalité, qui peuvent tous deux être lus comme des zones du profil de performance ci-dessous.
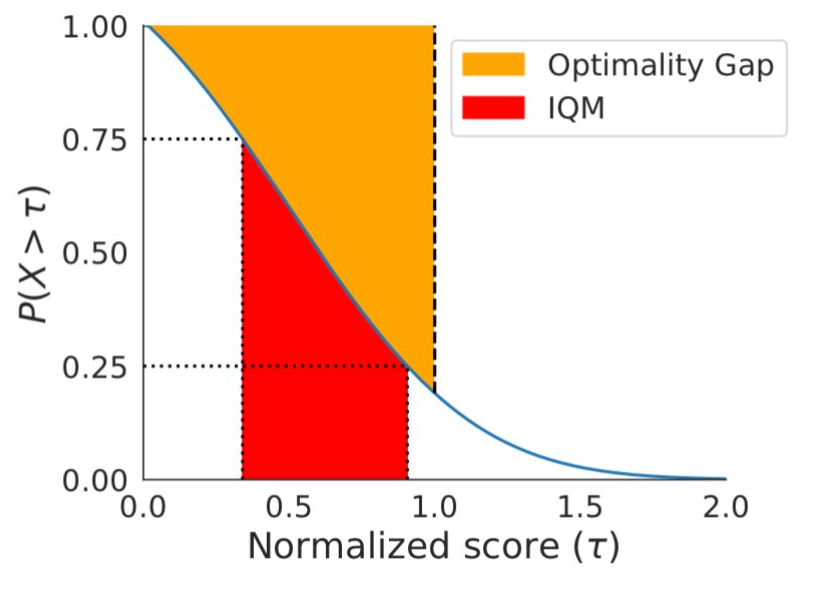
Solution de remplacement à la médiane et à la moyenne, la moyenne interquartile correspond au score moyen de 50 % des séquences combinées (valeurs du milieu) pour l’ensemble des tâches. Elle est plus robuste aux valeurs atypiques que la moyenne, constitue un meilleur indicateur des performances globales que la médiane et donne lieu à des intervalles de confiance plus petits, ce qui nécessite moins d’essais pour prétendre à des améliorations. L’écart d’optimalité est une autre option pour remplacer la moyenne. Il mesure la distance qui sépare un algorithme de la performance optimale.
Pour comparer directement deux algorithmes, une autre métrique à prendre en compte est la probabilité moyenne d’amélioration, qui décrit la probabilité d’une amélioration par rapport à la ligne de base, quelle que soit sa taille. Cette métrique est calculée à l’aide du test U de Mann-Whitney, en faisant la moyenne des tâches.
Réévaluer l’évaluation
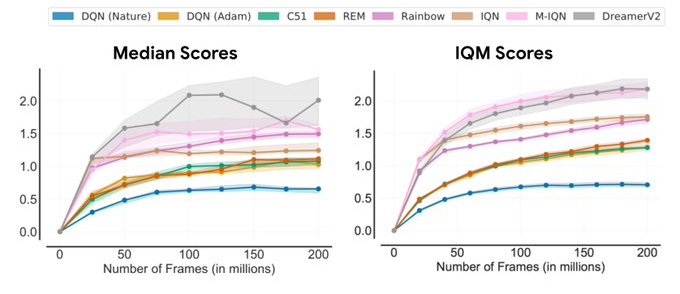
À l’aide des outils d’évaluation ci-dessus, nous avons réexaminé les évaluations de performance d’algorithmes d’apprentissage par renforcement existants à partir de méthodes couramment utilisées, révélant ainsi des incohérences. Par exemple, dans l’Arcade Learning Environment (ALE), une référence reconnue en apprentissage par renforcement, le classement de la performance des algorithmes change selon la métrique agrégée utilisée. Étant donné que les profils de performance donnent une image complète, ils illustrent souvent la raison de ces incohérences.
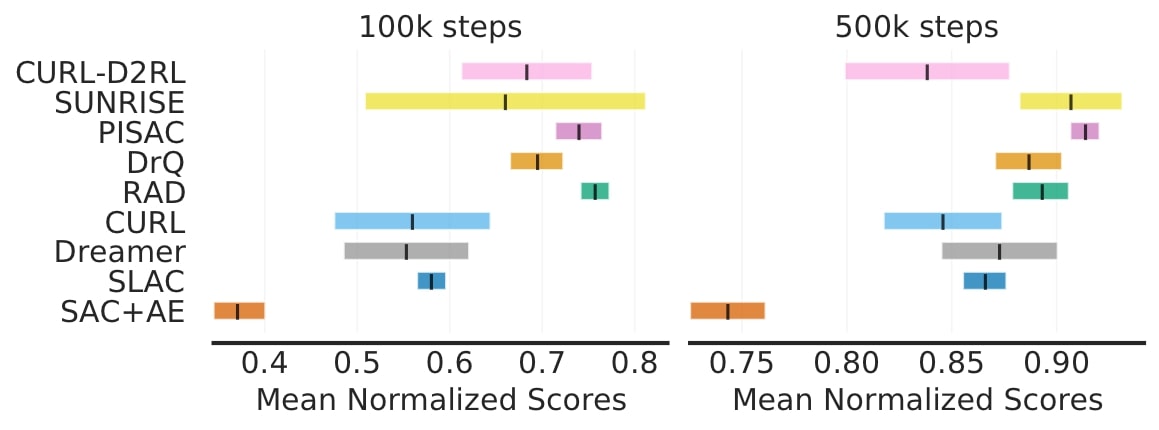
Sur DM Control, un test de contrôle continu populaire, il y a de grands chevauchements dans les intervalles de confiance à 95 % des scores moyens normalisés pour la plupart des algorithmes.
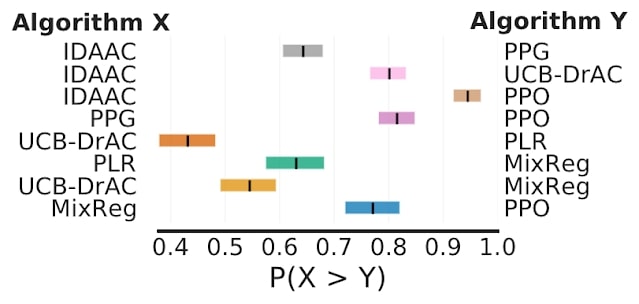
Enfin, sur Procgen, qui évalue la généralisation en apprentissage par renforcement, la probabilité moyenne d’amélioration montre que certaines améliorations rapportées ne sont probables qu’à 50-70 %, ce qui suggère qu’elles pourraient être fausses.
Conclusion
Nos résultats sur des tests de performance de l’apprentissage par renforcement profond couramment utilisés montrent que les questions statistiques peuvent avoir une grande influence sur les résultats rapportés. Dans ce travail, nous jetons un regard neuf sur l’évaluation afin d’améliorer l’interprétation des résultats rapportés et de standardiser les rapports expérimentaux. Nous aimerions souligner l’importance pour de publier des articles qui fournissent des résultats pour toutes les séquences afin de permettre de futures analyses statistiques. Pour renforcer la confiance dans vos résultats, veuillez consulter notre bibliothèque RLiable et le guide collaboratif de démarrage.
Remerciements
Ce travail a été réalisé en collaboration avec Max Schwarzer, Aaron Courville et Marc G. Bellemare. Nous tenons à remercier Tom Small pour l’animation utilisée dans ce blogue. Nous sommes également reconnaissants pour les commentaires de membres de Google Research, Google Brain Team et DeepMind.