Résumé
Pour comprendre ce blogue, une bonne connaissance des réseaux de neurones récurrents et de l’apprentissage par descente de gradient basé sur la rétropropagation à travers le temps est recommandée. L’élaboration de règles d’apprentissage biologiquement plausibles est intéressante pour répondre aux questions de neuroscience sur la façon dont le cerveau apprend et pour rechercher des stratégies de formation plus efficaces pour les réseaux de neurones artificiels. Cependant, les propriétés de généralisation des solutions trouvées par ces règles sont fortement négligées. Dans cet ouvrage, nous avons apporté un concept clé d’optimisation théorique de l’apprentissage automatique (courbure du paysage de la fonction de perte) pour étudier les propriétés de généralisation des systèmes d’apprentissage biologique. Nous avons d’abord démontré de manière empirique que les règles actuelles d’attribution temporelle de crédit biologiquement plausibles obtiennent un rendement de généralisation inférieur à celui des règles d’apprentissage profond. Nous avons ensuite dérivé un théorème, basé sur la courbure du paysage de la fonction de perte, pour expliquer la cause sous-jacente de ce phénomène. Enfin, nous avons suggéré des solutions potentielles qui pourraient être utilisées par le cerveau pour atténuer cet effet. Cet ouvrage a été présenté à la conférence NeurIPS 2022.
Auteurs de l’article : Yuhan Helena Liu, Arna Ghosh, Blake Aaron Richards, Eric Shea-Brown, Guillaume Lajoie
Introduction
Qu’est-ce que l’attribution temporelle de crédit et comment la résoudre dans les réseaux de neurones récurrents artificiels et biologiques?
Nous nous concentrons sur les réseaux de neurones récurrents (RNR) parce qu’ils ont été largement utilisés pour modéliser le cerveau. Les RNR peuvent être entraînés en ajustant les paramètres (généralement les poids de connexion, W, entre les neurones) pour apprendre les patrons d’entrée/sortie ciblés pour résoudre une tâche de calcul. La proximité du réseau avec la cible peut être quantifiée par une fonction de perte L.
Dans les RNR, l’ajustement des poids pour réduire cette fonction de perte L implique la résolution du problème d’attribution temporelle de crédit sous-jacent : l’attribution fiable du crédit (ou du blâme) à chaque poids en déterminant la contribution de tous les états neuronaux antérieurs à l’erreur observée au temps présent. Par exemple, supposons que vous jouez au baseball et que vous percevez que vous avez mal frappé la balle. Laquelle de vos 100 billions de synapses est à blâmer?
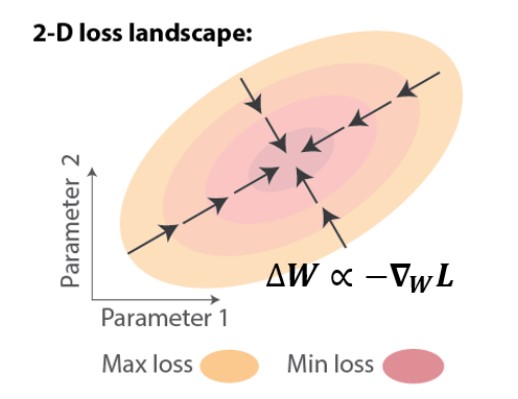
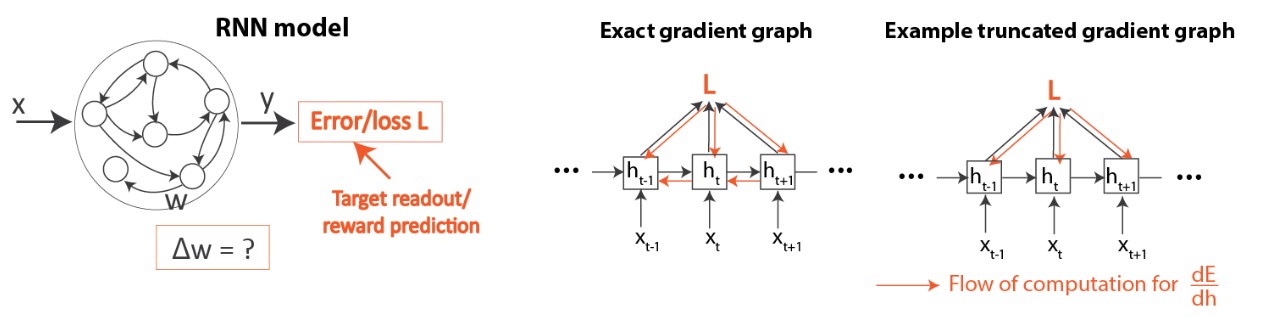
Dans les RNR artificiels, le problème d’attribution temporelle de crédit peut être résolu à l’aide de la rétropropagation à travers le temps (BPTT), qui applique la règle de dérivation en chaîne pour calculer le gradient exact de la perte par rapport aux poids, WL. On peut ensuite effectuer un apprentissage par descente de gradient, ce qui entraîne des améliorations itératives, c.-à-d. une réduction de la perte (Figure 1).
Dans les réseaux biologiques, cependant, il est difficile de résoudre le problème d’attribution temporelle de crédit. En raison du succès incroyable de l’entraînement de réseaux de neurones artificiels, les neuroscientifiques informatiques ont adopté une approche normative et se sont tournés vers la BPTT pour s’inspirer. Le problème avec cette approche est que la BPTT n’est pas biologiquement plausible, comme expliqué ci-dessous.
Qu’est-ce que la plausibilité biologique et pourquoi est-elle importante?
« Biologiquement plausible » signifie qu’aucune contrainte biologique connue n’est violée. Ce que l’on sait, c’est que le cerveau résout l’attribution temporelle de crédit à l’aide d’une règle d’apprentissage locale: chaque synapse ajuste sa force en utilisant uniquement l’information qui lui est physiquement disponible, y compris l’activité des deux neurones connectés par les synapses et tout signal neuromodulateur reflétant les récompenses et les erreurs. Par conséquent, la BPTT n’est pas biologiquement plausible parce qu’elle exige des informations non locales coûteuses et inaccessibles aux circuits de neurones [1]: pour utiliser la règle de dérivation en chaîne, il faudrait que les neurones artificiels suivent constamment l’activité synaptique de tous les neurones du réseau. En découvrant comment les règles locales peuvent mener à une attribution temporelle de crédit réussie, nous pourrions non seulement mieux comprendre comment le cerveau apprend, mais cela permettrait également un apprentissage plus écoénergétique sur les puces neuromorphiques, évitant les coûts de communication de la BPTT.
Quels sont les algorithmes existants d’attribution temporelle de crédit biologiquement plausibles? Dans quelle mesure sont-ils performants?
Les approches les plus efficaces pour mettre en œuvre des mécanismes d’attribution temporelle de crédit biologiquement plausibles ont été basées sur des gradients approximatifs [2-5]. Ces approches consistent à tronquer le gradient exact pour obéir à la contrainte de localité. Sur le plan géométrique du paysage de la fonction de perte, les mises à jour de poids utilisant l’apprentissage par descente de gradient approximatif pointent dans une direction qui suit partiellement le gradient, ce qui pourrait toujours entraîner une réduction de la perte si les mises à jour ont une composante positive dans la direction du gradient (Figure 2, gauche). Malgré la capacité de ces règles d’approximation à s’approcher de l’objectif de la tâche, on sait peu de choses sur l’impact qu’elles auraient sur la généralisation (Figure 2, droite). Par exemple, si nous testons avec des données perturbées reflétées comme un changement dans le paysage de la fonction de perte, comment le réseau entraîné selon ces règles fonctionnerait-il?
Question principale
Cela nous amène à notre question principale : quelles sont les propriétés de généralisation des règles d’attribution temporelle de crédit biologiquement plausibles? Pour simplifier, la généralisation fait référence à la capacité d’un modèle entraîné à s’adapter à des données auparavant inobservées, qui peuvent provenir de données retenues lors de l’entraînement ou qui sont tirées d’une autre distribution.
Approche
Approche fondée sur la théorie de l’apprentissage profond
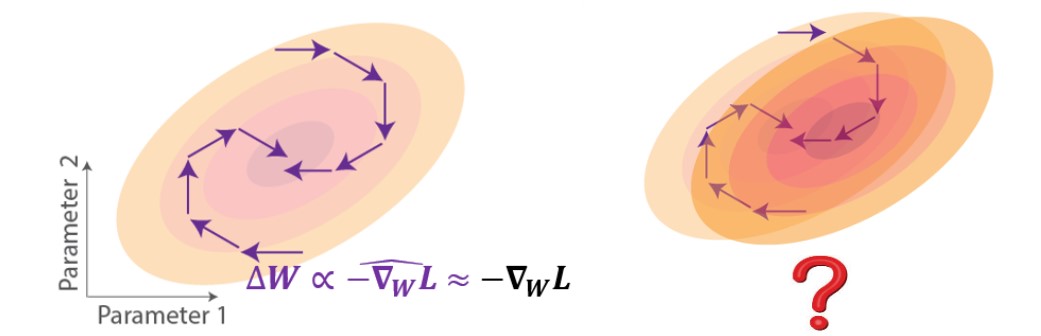
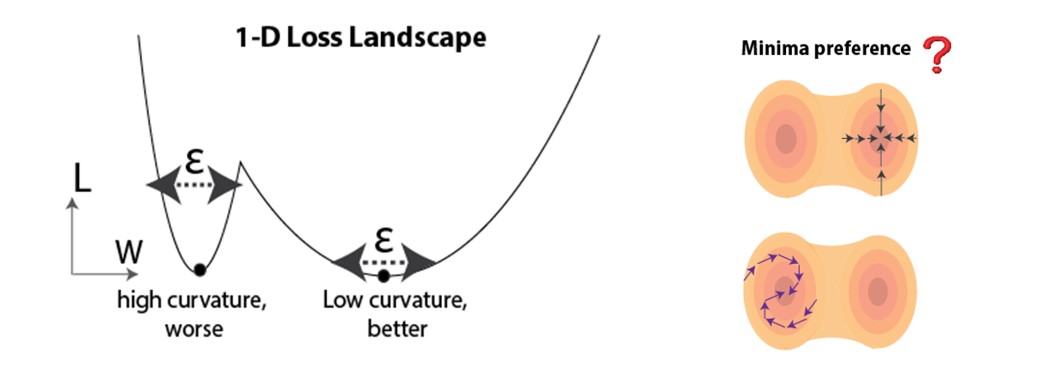
Nous tirons parti des progrès récents de la communauté de l’apprentissage profond : en tant que principal outil théorique pour prédire la généralisation, nous utilisons la courbure du paysage de la fonction de perte au point de solution (minima dans l’espace des paramètres) obtenue à partir de l’apprentissage. Il a été démontré à la fois empiriquement et théoriquement que des minima plus plats peuvent être plus favorables à la généralisation [6-13]. Une intuition est démontrée à la Figure 3 (à gauche), où des minima plus plats sont moins sensibles aux perturbations (p. ex., le bruit pendant l’essai). Étant donné qu’il existe généralement de nombreux minima dans les réseaux surparamétrés, nous nous demandons si les règles d’attribution temporelle de crédit biologiquement plausibles biaisent systématiquement l’apprentissage pour converger vers des minima plus plats ou plus pointus (Figure 3, à droite).
Aperçu de la configuration
La Figure 4 donne un aperçu de notre réseau et de sa configuration d’apprentissage. Comme mentionné dans l’introduction, nous examinons l’apprentissage dans les RNR (Figure 4, à gauche). Nous comparons l’algorithme d’apprentissage profond standard (BPTT) et les règles existantes d’attribution temporelle de crédit biologiquement plausibles [2-5], qui ont toutes été basées sur des troncatures de gradient, comme mentionné ci-dessus (Figure 4, droite). Veuillez consulter l’article pour obtenir des détails sur le fonctionnement de ces algorithmes.
Constats
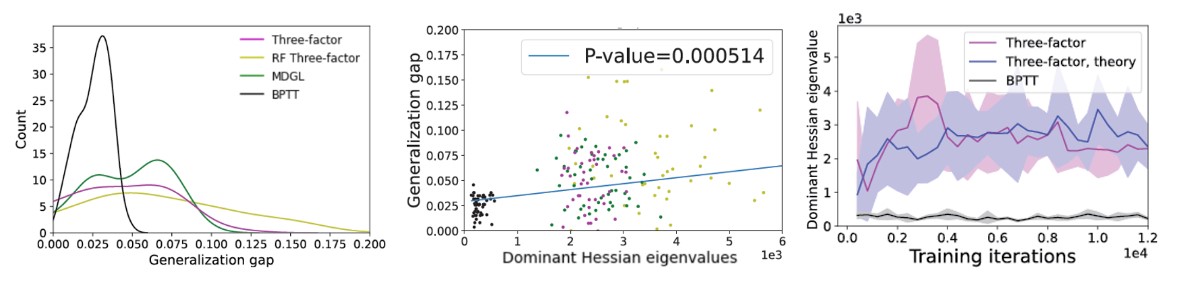
Nous combinons des analyses théoriques et des simulations empiriques à travers plusieurs références bien connues en matière d’apprentissage automatique et de neurosciences. La principale conclusion de notre étude est que les règles d’apprentissage biologiquement plausibles existantes dans les RNR obtiennent une performance de généralisation pire (Figure 5, gauche), ce qui est cohérent avec leur tendance à converger vers des régions à forte courbure dans l’environnement des pertes (Figure 5, milieu). À l’aide de la théorie des systèmes dynamiques, nous avons ensuite dérivé un théorème attribuant le comportement de convergence de la courbure à l’erreur d’approximation du gradient dans certaines conditions (voir l’article). Bien qu’il ait été démontré que le bruit provenant de la descente du gradient stochastique peut contribuer à échapper aux minima pointus [7,10], l’erreur d’approximation du gradient due à la troncature peut avoir des propriétés différentes (voir l’article). Notre prédiction théorique correspond aux résultats de notre simulation (Figure 5, à droite). Nous avons aussi suggéré des solutions potentielles qui pourraient être utilisées par le cerveau pour atténuer cet effet.
Prochaines étapes
Notre étude constitue une première étape vers la compréhension de la généralisation biologique à l’aide de méthodes d’apprentissage profond et soulève de nombreuses questions passionnantes pour les futures recherches mêlant l’apprentissage profond et la neuroscience informatique. Ces questions incluent les suivantes : (1) à mesure que la communauté de l’apprentissage profond améliore les outils théoriques pour étudier la généralisation, comment peuvent-ils être exploités pour étudier les systèmes d’apprentissage biologique? (2) Quel est l’effet sur la généralisation des différents types de bruit qui apparaissent dans les systèmes biologiques? (3) Comment pouvons-nous tirer davantage parti des outils d’apprentissage profond pour générer des prédictions vérifiables sur la façon dont différentes composantes biologiques peuvent interagir avec les règles d’apprentissage pour améliorer la généralisation?
Pour en savoir plus, veuillez consulter notre article arXiv paper [14].
Références
[1] Richards et al., Nat Neurosci, 2019. [2] Murray, eLife, 2019. [3] Bellec et al., Nat Commun, 2020. [4] Liu et al., PNAS, 2021. [5] Marschall et al., JMLR, 2020. [6] Hochreiter and Schmidhuber, Neural Comput, 1997. [7] Keskar et al., ICLR, 2017. [8] Jastrezebski et al., ICLR, 2018. [9] Yao et al., NeurIPS 2019. [10] Xie et al., ICLR 2021. [11] Tsuzuku et al., ICML, 2020. [12] Petzka et al., NeurIPS, 2021. [13] Jiang et al., ICLR 2020. [14] Liu et al., NeurIPS, 2022.