Note de la rédaction : Cet article a été initialement publié sur le site Web personnel de Yoshua Bengio.
J’ai rarement été aussi emballé par une nouvelle orientation de recherche. Nous les appelons réseaux de flot génératifs ou GFlowNets, pour Generative Flow Networks. Ils se situent quelque part au carrefour de l’apprentissage par renforcement, des modèles génératifs profonds et de la modélisation probabiliste basée sur les fonctions d’énergie. Ils sont également liés aux modèles variationnels et à l’inférence probabiliste, et j’estime qu’ils ouvrent de nouveaux horizons à la modélisation bayésienne non paramétrique, à l’apprentissage actif génératif et à l’apprentissage non supervisé ou autosupervisé (self-supervised) de représentations abstraites pour démêler les facteurs causaux explicatifs et les mécanismes qui les relient. Ce que je trouve passionnant, c’est qu’ils ouvrent de nombreuses portes, notamment pour mettre en œuvre les biais inductifs du système 2 dont j’ai parlé dans plusieurs de mes articles et conférences depuis 2017. Selon moi, ces biais inductifs sont importants pour intégrer la causalité et traiter la généralisation hors distribution de manière rationnelle. Ils permettent aux réseaux de neurones de modéliser des distributions sur des structures de données comme les graphes (par exemple, les molécules, comme dans l’article de NeurIPS, et les graphes explicatifs et causaux, dans les travaux en cours et à venir), de les échantillonner et d’estimer toutes sortes de quantités probabilistes (comme les énergies libres, les probabilités conditionnelles sur des sous-ensembles arbitraires de variables ou les fonctions de partition) qui semblent autrement insolubles (et approximées par chaînes de Markov Monte-Carlo).
En même temps, il s’agit d’une nouvelle bête qui, au départ, peut sembler étrange. Une bête que nous devons apprivoiser, pour laquelle les progrès des algorithmes d’optimisation appropriés sont encore rapides (voir cet article, par exemple) et dont les possibilités, mises en lumière par les recherches à venir, se feront probablement nombreuses. Plusieurs de mes étudiants ont mis du temps à digérer les nouveaux concepts, mais cela en vaut la peine. Une rafale de nouveaux articles sera publiée incessamment et d’autres sont en préparation, car les esprits créatifs sont en ébullition. Mon fils Emmanuel a dirigé le premier article sur les réseaux de flot génératifs et a écrit un article de blogue à ce sujet pour accompagner notre article de NeurIPS 2021, l’article original sur les GFlowNets. Plus récemment, j’ai écrit un tutoriel pour expliquer les idées de base, et vous y trouverez aussi tous les articles récents à ce propos. Vous pouvez aussi consulter cet exposé plutôt technique que j’ai récemment présenté à l’interne à Mila et cette discussion plus accessible et philosophique intitulée GFlowNets, Consciousness & Causality. Elle présente un aperçu de l’évolution potentielle des réseaux de flot génératifs qui visent à combler le fossé entre l’IA de pointe et l’intelligence humaine en introduisant les biais inductifs du système 2 dans les réseaux de neurones. Bonne découverte !
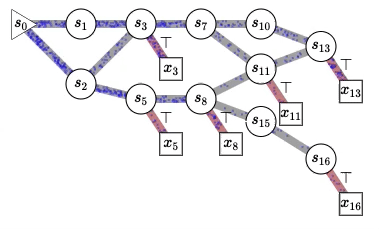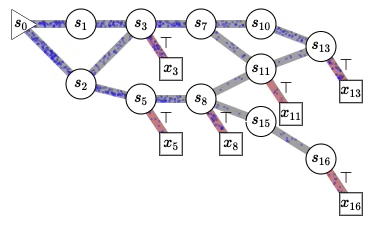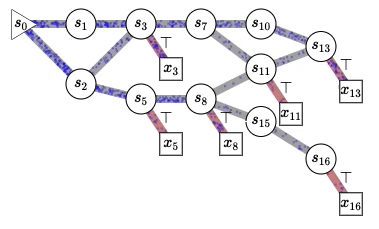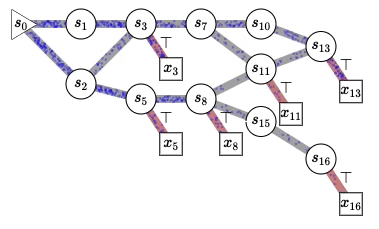
Cette figure illustre pourquoi nous utilisons le mot « flot » dans les réseaux de flot génératifs. Nous faisons référence au flot de probabilités non normalisées, semblable au flot de l’eau qui s’écoule d’un état initial (s0 à gauche) dans un graphe acyclique dirigé (comme il peut être exponentiellement grand, nous n’avons pas besoin de le représenter de manière explicite dans les ordinateurs) dont les trajectoires correspondent à toutes les séquences d’actions possibles (actions qui déterminent les transitions d’état) afin de construire séquentiellement des objets compliqués comme des graphes moléculaires, des graphes causaux, des explications pour une scène ou (et c’est là la véritable inspiration) les pensées de notre esprit. Les nœuds carrés avec des transitions rouges correspondent aux états terminaux, des objets finis échantillonnés selon une politique stochastique qui choisit les enfants de chaque état (les états accessibles en franchissant un segment en aval) avec une probabilité proportionnelle au flot dans l’arête sortante correspondante. Il est intéressant de noter que cela permet de générer un ensemble diversifié d’échantillons sans faire face à ce que je pensais être un défi insoluble : passer d’un mode à l’autre (mode mixing) avec les méthodes MCMC. Ce qui est remarquable avec ce cadre, c’est qu’il nous indique comment entraîner une politique qui échantillonne les objets construits avec la probabilité souhaitée (précisée par une fonction d’énergie, une fonction de probabilité non normalisée ou une fonction de récompense, que nous pouvons aussi apprendre) et comment estimer les constantes de normalisation et les probabilités conditionnelles correspondantes pour n’importe quel sous-ensemble de variables abstraites. Vous en apprendrez plus dans le tutoriel. 🙂