L’entraînement des réseaux neuronaux profonds passe habituellement par la minimisation du risque empirique, un procédé qui consiste à optimiser un modèle de manière à ce qu’il fonctionne efficacement par rapport aux points de données vus au cours de l’apprentissage. Le réseau obtient des résultats d’une grande justesse relativement à des points de données analogues à ceux qui ont été vus, mais souvent médiocres relativement aux points de données éloignés de la distribution des étiquettes d’apprentissage (car sa capacité de généralisation n’est que faiblement limitée par l’architecture).
Pour illustrer ce propos de manière plus concrète, prenons le cas simple d’un apprentissage portant sur des spirales 2D assorties d’un petit nombre d’échantillons étiquetés. L’une des couches cachées de l’architecture ne comporte que deux dimensions, de sorte que nous pouvons visualiser directement ce qui s’y passe.

Même si cet exemple ne comporte que deux dimensions, il illustre plusieurs problèmes fondamentaux qui se posent dans le cadre habituel de la minimisation du risque empirique.
- Le modèle possède un degré de certitude très élevé dans la quasi-totalité de l’espace, soit à la fois dans l’espace d’entrée et dans l’espace caché (les parties en rouge ou en bleu indiquent un degré de certitude élevé).
- La frontière de décision avoisine de très près les points de données réels.
- L’encodage des points d’apprentissage occupe une grande partie de l’espace caché.
Pour résoudre ces problèmes, nous comptons faire porter l’apprentissage sur des combinaisons d’attributs tirées de divers exemples. Bien qu’il s’agisse d’un axe de recherche en cours de développement, nous proposons d’employer un procédé simple appelé Manifold Mixup:
- Nous faisons appel à une simple interpolation linéaire pour combiner les états cachés inhérents à des paires d’exemples. Bien que cette méthode ne tienne pas compte de toutes les combinaisons d’informations possibles, les travaux de recherche portant sur les représentations vectorielles continues montrent que les combinaisons linéaires d’états cachés peuvent revêtir une signification sémantique.
- Pour étiqueter ces points associés, nous appliquons le même procédé de combinaison linéaire des cibles aux paires d’exemples retenues (dans le cas de la perte d’entropie croisée, cela équivaut à effectuer une moyenne pondérée des pertes).
- Les couches de niveau supérieur ont un caractère plus abstrait et pourraient donc être mieux représentées par de simples interpolations linéaires. Par contre, elles escamotent plus de détails des données initiales. Pour éviter cet inconvénient, nous procédons au mélange sur une couche aléatoire pour chaque exemple.
L’espace mémoire et le temps de calcul sont des contraintes importantes tant pour les chercheurs que pour les praticiens. Or, le procédé Manifold Mixup ne requiert pratiquement aucune autre étape de calcul ou d’espace mémoire supplémentaire, puisqu’il n’exige que la combinaison des états cachés et des étiquettes de classe comme étape de calcul supplémentaire.
Comment cela fonctionne-t-il?
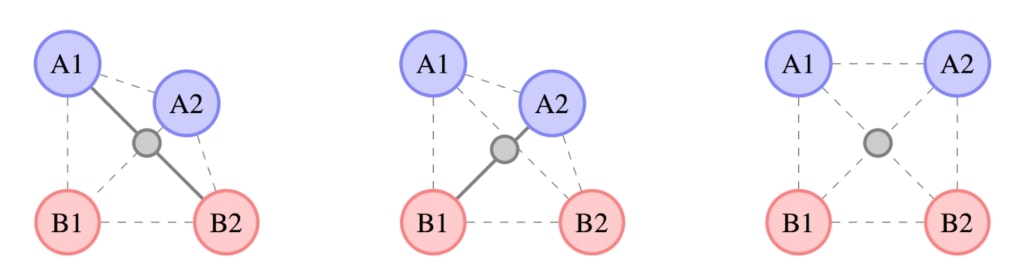
Le procédé Manifold Mixup peut être décrit en des termes très simples. Il ne fait appel qu’à deux hyperparamètres : alpha (le coefficient de mélange) et S (l’ensemble des couches qui composent le mélange).
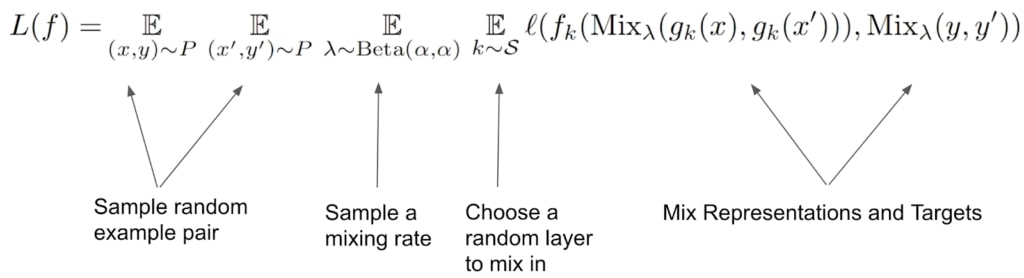
La figure suivante présente un diagramme illustrant le procédé Manifold Mixup.
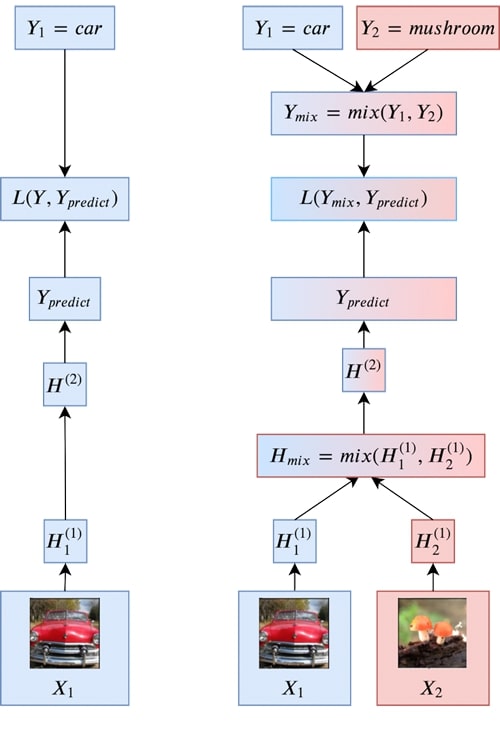
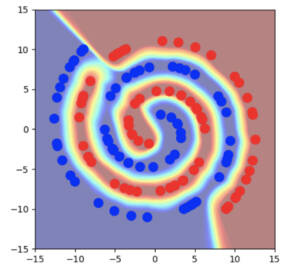
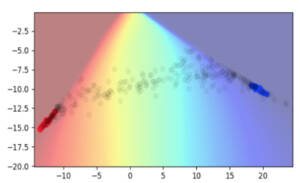
Pour revenir à l’exemple des spirales, on constate que la frontière de décision est beaucoup plus éloignée des points de données réels, tant dans l’espace d’entrée que dans l’espace caché. La zone d’incertitude, beaucoup plus grande, est également éloignée des points de données réels. Il est étonnant de constater que les états cachés sous-jacents aux points de données réels prennent un aspect très concentré. Dans cet exemple, ils tiennent pratiquement en un seul point!
Comment expliquer cette redistribution des états cachés lors de l’apprentissage selon le procédé Manifold Mixup? Si elle n’est pas évidente à première vue, cette particularité devient plus flagrante si l’on considère les types de données qui s’inscrivent le mieux dans un modèle linéaire. Aucune direction pointant entre différentes classes ne devrait présenter de variabilité intra-classe. Ainsi, la variabilité intra-classe et la variabilité inter-classe sont ramenées à des sous-espaces linéaires orthogonaux. Dans un problème de classification binaire comportant un espace caché 2D, cela fait en sorte que chaque classe est ramenée à un point unique.
Nous avons d’abord observé ce changement drastique en utilisant le procédé Manifold Mixup pour résoudre des problèmes jouets en 2D. Puis, nous nous sommes demandé si cet effet de concentration survenait également dans des espaces de plus grande dimension et, le cas échéant, quelle en était la signification.
Pour analyser le comportement des espaces de plus grande dimension de manière empirique, nous nous sommes tournés vers la décomposition en valeurs singulières. Ce procédé consiste à adapter des ellipses à un ensemble de points situés dans un espace (potentiellement de grande dimension), puis à étudier le nombre de dimensions de l’ellipse qui présentent une variabilité importante. On appelle la longueur des axes de l’ellipse « valeurs singulières ». Si toutes les valeurs singulières sont identiques, les points de données forment ce qui s’apparente à une sphère. Par contre, s’il y a une seule grande valeur singulière, alors les points de données tracent à peu près la forme d’un tube étroit en ellipse. Dans les faits, on constate que le procédé Manifold Mixup influe grandement sur cette approximation elliptique des états cachés. Plus précisément, le recours à ce procédé réduit considérablement le nombre de directions dans l’espace caché présentant une variabilité importante.
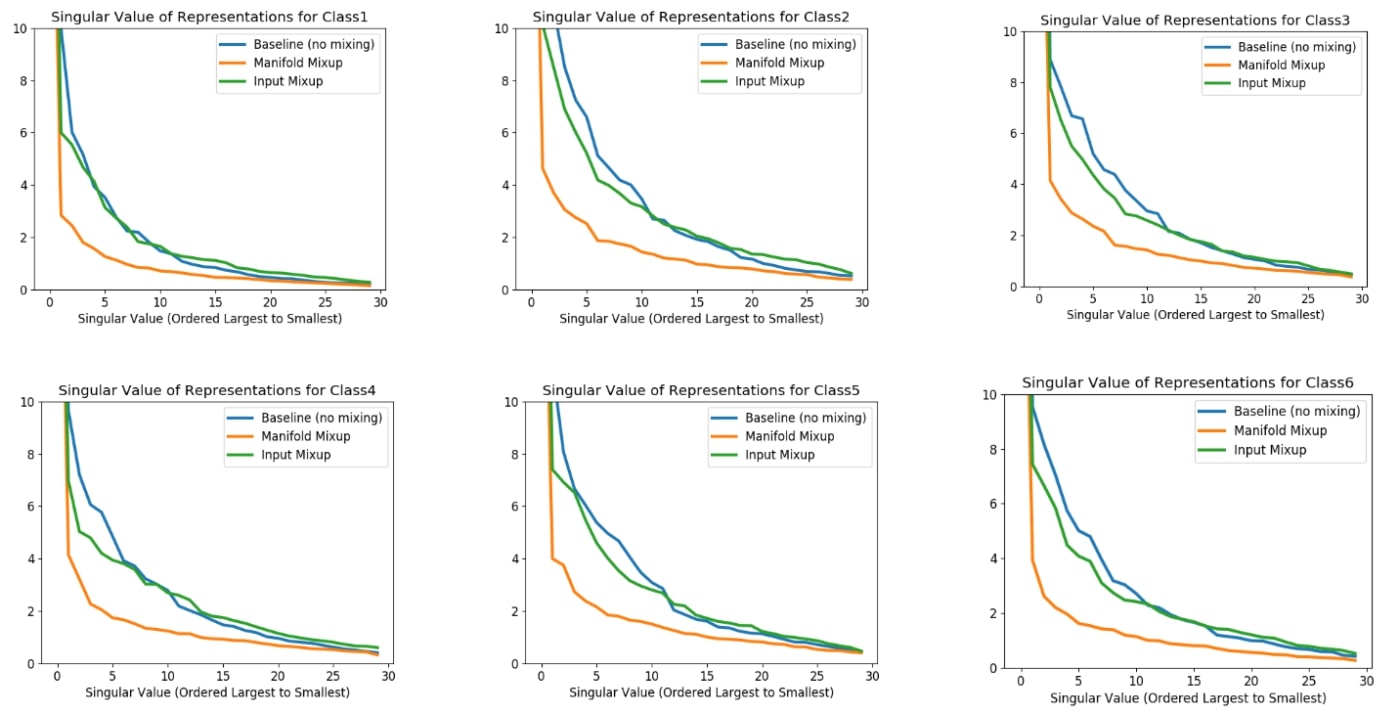
Résultats d'analyse
Non seulement le procédé Manifold Mixup possède des caractéristiques intéressantes, mais il s’avère un outil de régularisation efficace dans le cadre de tâches concrètes. Nous avons montré ici qu’il surpasse d’autres outils de régularisation concurrents tels que Dropout, CutOut et Mixup (voir l’étude complète pour plus de précisions).
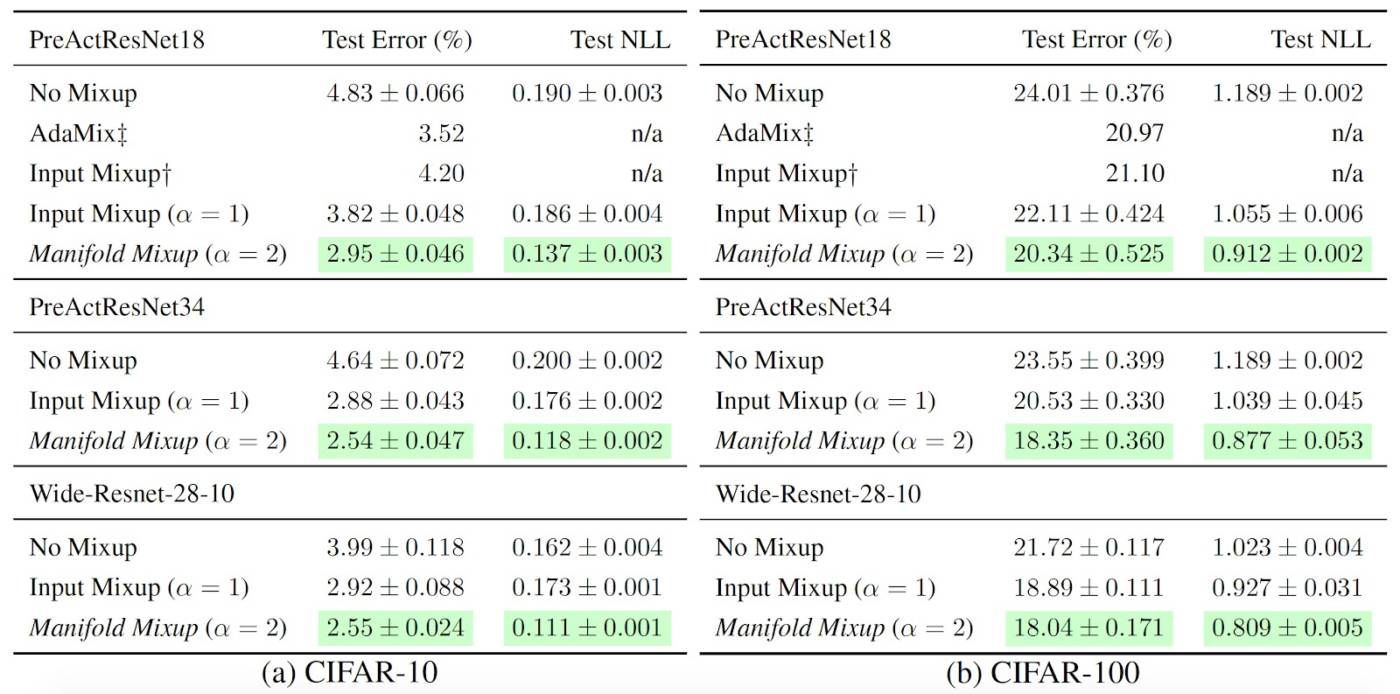
Il convient de noter que, bien souvent, le procédé Manifold Mixup améliore grandement la vraisemblance sur l’ensemble d’évaluation – ce qui, d’après nous, tient au fait que le modèle présente une certitude moindre, loin de la distribution des données d’apprentissage. Ce facteur est d’une importance cruciale quand vient le temps d’obtenir des résultats probants, car des points classés avec certitude, mais de façon erronée, peuvent sérieusement compromettre la vraisemblance sur l’ensemble d’évaluation (en fait, un seul point suffit à ramener la vraisemblance à zéro).
Par ailleurs, le procédé Manifold Mixup se révèle très efficace quant à ses deux hyperparamètres : le choix des couches à mélanger et le coefficient de mélange (alpha).
Développements récents
Malgré son apparition relativement récente (ICML, 2019), le procédé Manifold Mixup a connu plusieurs avancées enthousiasmantes. Plusieurs projets de recherche appliquée ont mis ce procédé à contribution avec succès.
Ainsi, Bastien et ses collaborateurs (2019) ont démontré que la reconnaissance des textes manuscrits gagnait en fidélité grâce au procédé Manifold Mixup. Fait notable, l’équipe a utilisé une fonction de perte structurée, répartie entre différents exemples, au lieu de mélanger directement les cibles comme nous l’avons fait dans notre étude. Mangla et ses collaborateurs (2019) ont conjugué pour leur part le procédé Manifold Mixup à des stratégies d’autocontrôle (telles que la prédiction de la rotation) pour obtenir des résultats avancés dans des tâches de classification d’images pour l’apprentissage few-shot. Verma et ses collaborateurs (2019), quant à eux, ont proposé de former un réseau entièrement connecté en utilisant le procédé Manifold Mixup conjointement à des réseaux neuronaux de graphes pour les tâches de classification des nœuds. Ils font état d’améliorations substantielles des résultats, dont des résultats exceptionnels relativement à plusieurs ensembles de données concurrents. Enfin, Roth et ses collaborateurs (2020) ont étudié l’aplanissement dans le contexte de l’apprentissage par transfert en se fondant sur la théorie Manifold Mixup.
This blog post is based on our paper:
Manifold Mixup: Better Representations by Interpolating Hidden States
Vikas Verma, Alex Lamb, Christopher Beckham, Amir Najafi, Ioannis Mitliagkas, Aaron Courville, David Lopez-Paz, Yoshua Bengio
ICML 2019 (https://arxiv.org/abs/1806.05236)
Références
[1] Moysset, Bastien, and Ronaldo Messina. "Manifold Mixup improves text recognition with CTC loss." 2019 International Conference on Document Analysis and Recognition (ICDAR). IEEE, 2019.
[2]Mangla, Puneet, et al. "Charting the right manifold: Manifold mixup for few-shot learning." The IEEE Winter Conference on Applications of Computer Vision. 2020.
[3] Verma, Vikas, et al. "Graphmix: Regularized training of graph neural networks for semi-supervised learning." arXiv preprint arXiv:1909.11715 (2019).
[4] Roth, Karsten, et al. "Revisiting training strategies and generalization performance in deep metric learning." arXiv preprint arXiv:2002.08473 (2020).