Le succès des algorithmes d’apprentissage auto-supervisé (AAS) a radicalement changé l’entraînement des réseaux de neurones profonds. Grâce à des architectures et des objectifs d’entraînement bien conçus, les modèles basés sur l’AAS apprennent des représentations « utiles » à partir de grands ensembles de données sans dépendance d’étiquette [Self-supervised learning: The dark matter of intelligence, Lecun et Misra, 2021] [Advancing Self-Supervised and Semi-Supervised Learning with SimCLR, Chen et Hinton, 2020].
Notamment, lorsque ces modèles sont réentraînés sur une tâche appropriée en aval, ils peuvent souvent atteindre des performances de pointe avec moins de données que les modèles supervisés. Toutefois, le succès des modèles basés sur l’AAS n’est pas garanti. En particulier, les algorithmes d’AAS nécessitent souvent une sélection minutieuse du modèle pour éviter l’effondrement des représentations [Understanding self-supervised Learning Dynamics without Contrastive Pairs, Tian, 2021]. De plus, il est difficile d’évaluer la qualité des représentations apprises, car il faut généralement du temps de calcul supplémentaire pour entraîner des couches linéaires à connecter ces représentations à de nouvelles données étiquetées.
Mesures de qualité des représentations agnostiques à la tâche
La thèse centrale de cette étude explore le point suivant :
Dans le domaine de la perception, comment déterminer efficacement la qualité des représentations apprises au moyen de l’AAS dans un large éventail de tâches potentielles en aval?
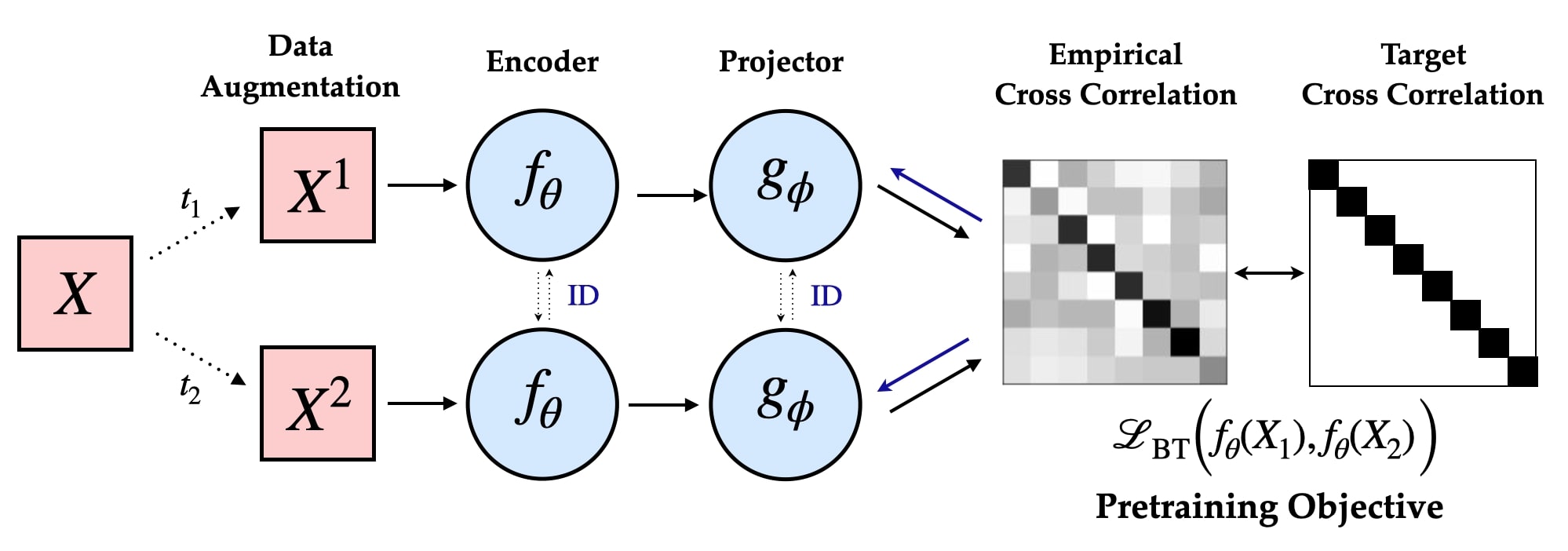
Les algorithmes d’AAS destinés à l’apprentissage des représentations entraînent généralement des encodeurs multivues qui intègrent un bias inductif dans l’espace latent par l’intermédiaire de l’objectif d’apprentissage (p. ex., algorithmes non contrastifs) [Barlow Twins: Self-Supervised Learning via Redundancy Reduction, Zbontar, 2021]
Pour répondre à cette question, il faut définir formellement la notion de qualité et examiner les estimateurs statistiques qui mesurent cette propriété sans nécessiter d’évaluation en aval. Au-delà de l’intérêt théorique, une telle métrique serait hautement souhaitable pour la sélection de modèle et la conception de nouveaux algorithmes d’AAS.
À la recherche d’une telle métrique, nous mettons l’accent sur l’une des machines d’apprentissage automatique les plus efficaces, à savoir le cerveau mammifère. L’organisation hiérarchique et distribuée des circuits de neurones, en particulier dans le cortex, fournit des représentations neuronales qui soutiennent de nombreux comportements dans plusieurs domaines. Elles soutiennent, par exemple, des comportements en aval, allant de la catégorisation des objets à la détection des mouvements et au contrôle moteur [Distributed hierarchical processing in the primate cerebral cortex, Felleman et Essen, 1991].
Les récentes avancées dans le domaine de la neuroscience des systèmes permettent d’enregistrer à grande échelle une telle activité neuronale. En enregistrant et en analysant la réponse aux stimuli visuels, les études High-dimensional geometry of population responses in the visual cortex [Stringer, 2018] et Increasing neural network robustness improves match to macaque V1 eigenspectrum, spatial frequency preference, and predictivity [Kong, 2022] constatent que les activations chez la souris et le singe macaque V1 présentent une structure géométrique caractéristique de l’information. En particulier, ces représentations sont hautement dimensionnelles, mais la quantité d’information codée dans les différentes directions principales varie considérablement. En particulier, cette variance (calculée en mesurant le spectre propre de la matrice de covariance empirique) est bien approximée par une distribution de la loi de puissance avec un coefficient de dégradation à peu près égal à 1, c.-à-d. que la valeur propre de la matrice de covariance est égale à 1/n.
Simultanément, les progrès de l’apprentissage automatique théorique permettent de mieux comprendre les limites de l’erreur de généralisation pour les modèles de régression linéaire dans les régimes surparamétrés. L’étude du surajustement bénin dans la régression linéaire [Benign Overfitting in Linear Regression, Bartlett, 2019] détermine que dans le régime infini-dimensionnel (d→∞) avec des attributs gaussiens, la norme minimale interpolant la règle de prédiction présente une bonne généralisation pour une gamme étroite de propriétés de la distribution des données. En particulier, le rang effectif de l’opérateur de covariance Cov(X) régit la généralisation en aval.
Mesure de la dégradation et de la généralisation du spectre propre
Inspirés par ces résultats, nous nous penchons plus profondément sur la structure des représentations apprises par des encodeurs bien entraînés. Un des aspects des encodeurs préentraînés est qu’ils apprennent une correspondance entre l’espace des caractéristiques fournies en entrée (de haute dimension) et un espace latent de dimension inférieure, par exemple fθ:Rd→Rk (généralement k<<d). Notre idée maîtresse repose sur l’étude des propriétés géométriques de l’espace latent des représentations en examinant la matrice (centrée) de covariance des attributs Cov(fθ)=Ex[fθ(x)fθ(x)⊤].
Les propriétés spectrales de Cov(fθ) sont cruciales, car elles nous renseignent sur l’ampleur de la variance dans différentes directions de l’espace latent. À titre d’exemple, considérons le cadre suivant : un grand ensemble de données non étiquetées (disons STL10) projeté dans un espace latent avec un encodeur déjà entraîné. Des directions précises dans l’espace latent codent une plus grande variabilité, souvent identifiées comme les composantes principales des représentations. Notre analyse porte sur les valeurs propres de la matrice de covariance de fθ(X).
En nous appuyant sur l’intuition issue de la régression linéaire, nous examinons de plus près Cov(fθ(X)) dans les architectures de réseaux de neurones canoniques. En particulier, nous sondons des modèles tels VGG [Very Deep Convolutional Networks for Large-Scale Image Recognition, Simonyan, 2014], ResNets [Deep Residual Learning for Image Recognition, He, 2016] et ViTs (Vision Transformers) [An Image is Worth 16×16 Words: Transformers for Image Recognition at Scale, Dosovitsky, 2020], qui sont préentraînés sur les ensembles de données CIFAR/ImageNet en fonction de différents objectifs d’apprentissage. En particulier, nous calculons le spectre propre, c.-à-d. la distribution des valeurs propres {λ1,λ2,…λn}, de la matrice de covariance des attributs empiriques.
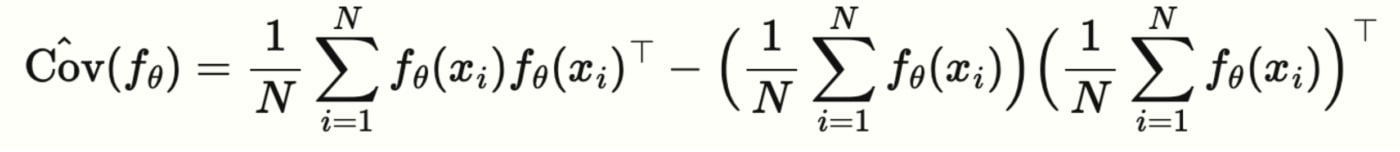
Par ailleurs, pour comprendre le rôle de l’objectif d’apprentissage, nous considérons des modèles de préentraînement avec entropie croisée standard (supervisés) : BYOL [Bootstrap your own latent: A new approach to self-supervised Learning, Grill, 2020], Barlow Twins [Barlow Twins: Self-Supervised Learning via Redundancy Reduction, Zbontar, 2021] (non contrastifs) et SimCLR [A Simple Framework for Contrastive Learning of Visual Representations, Chen, 2020] (contrastifs).
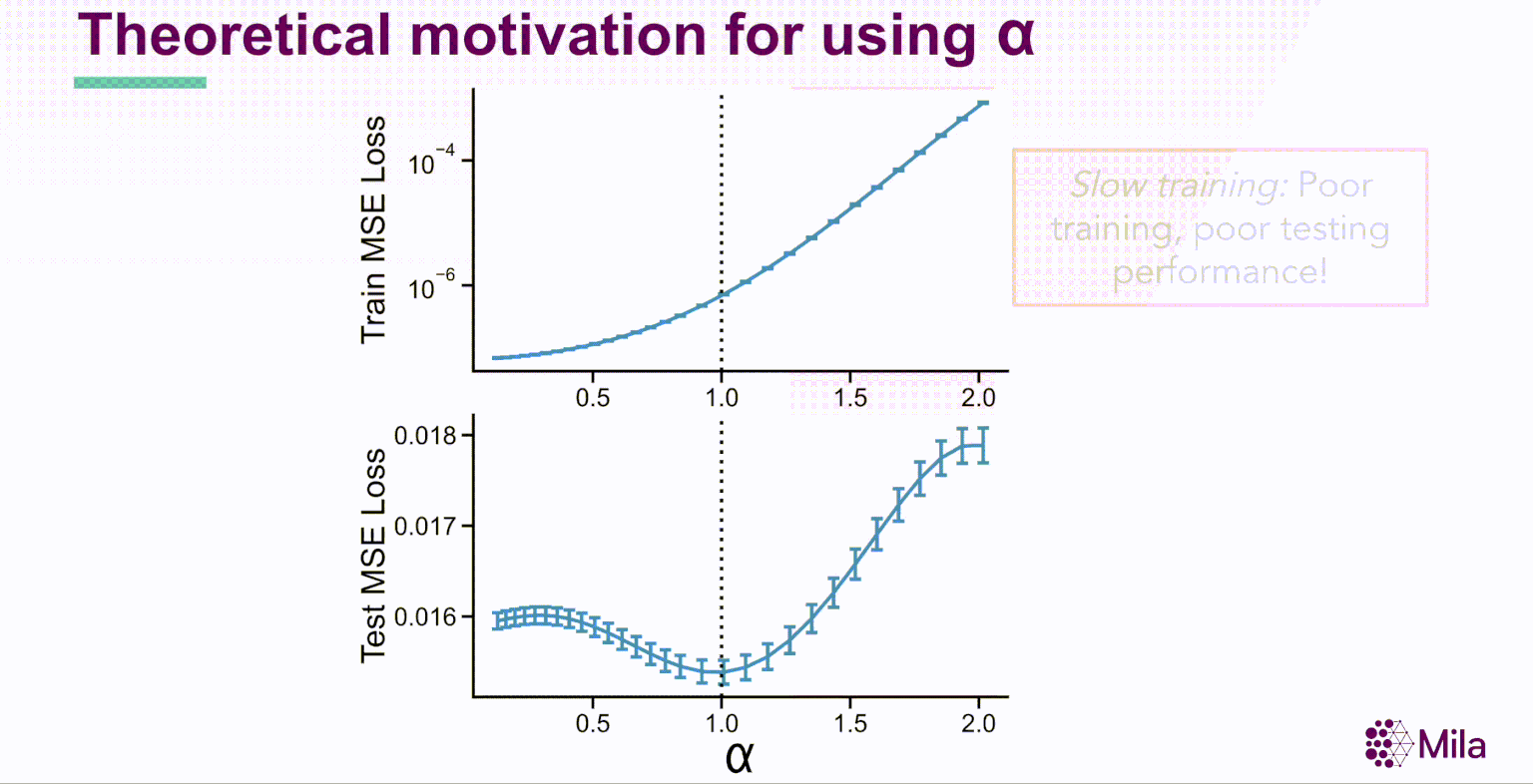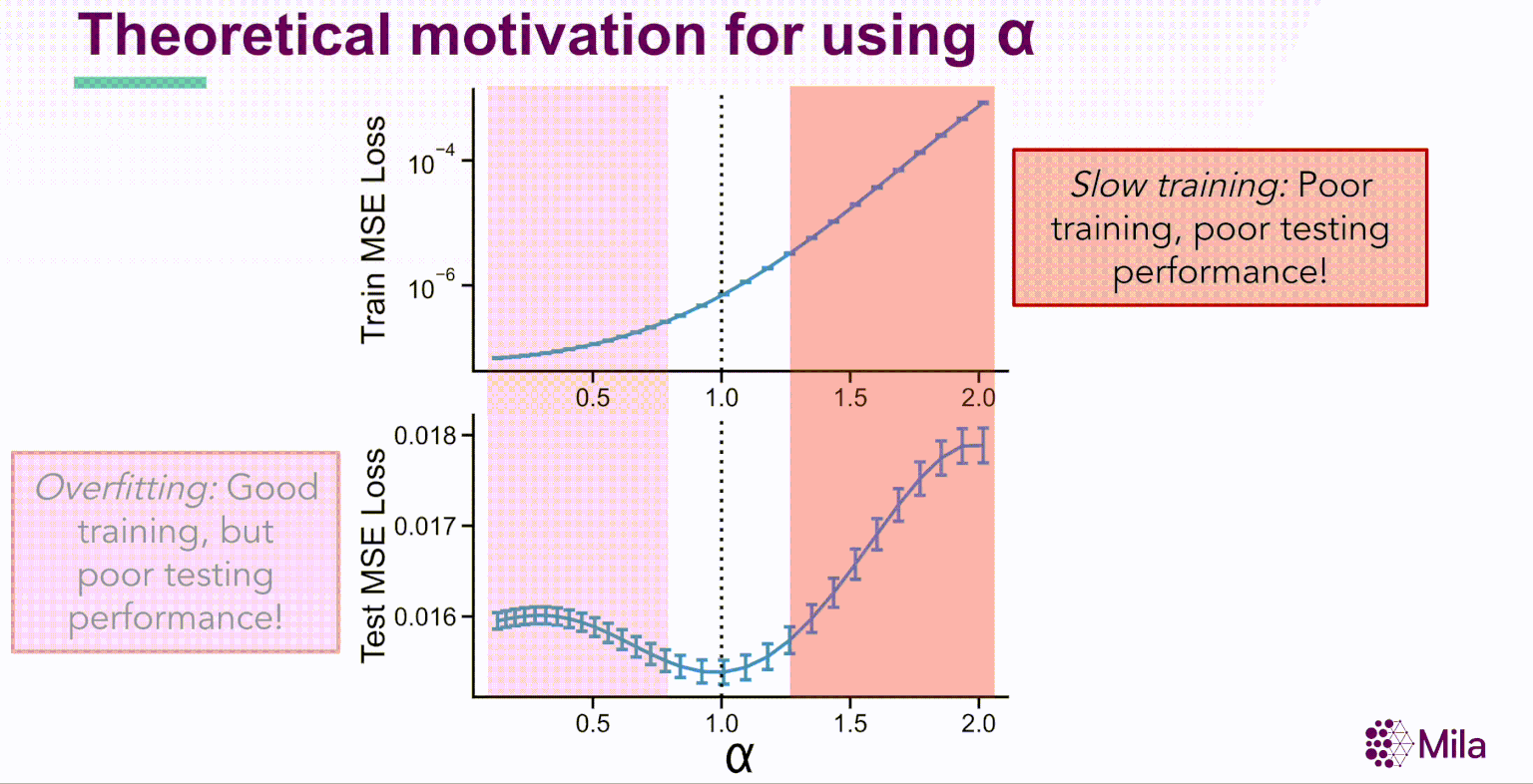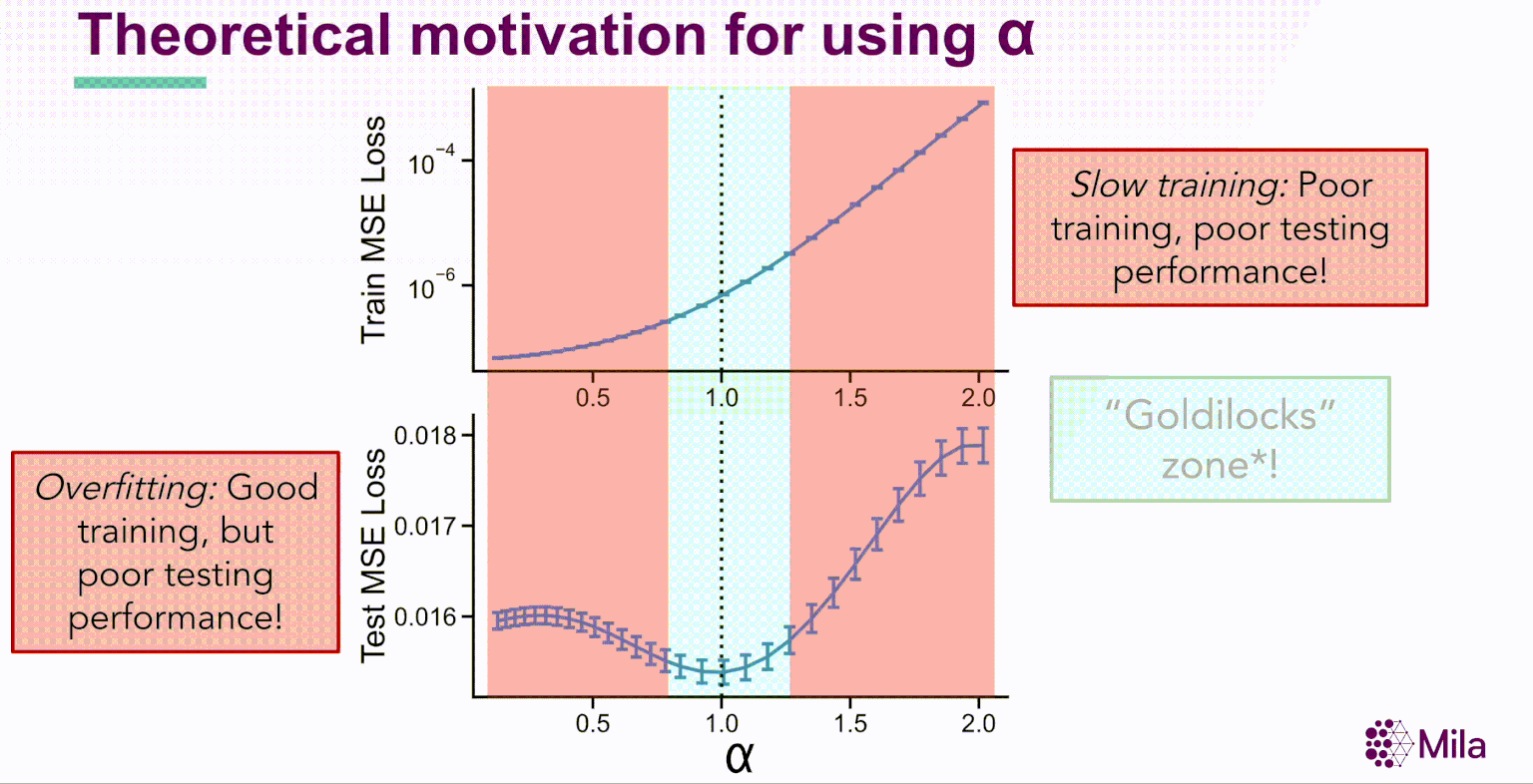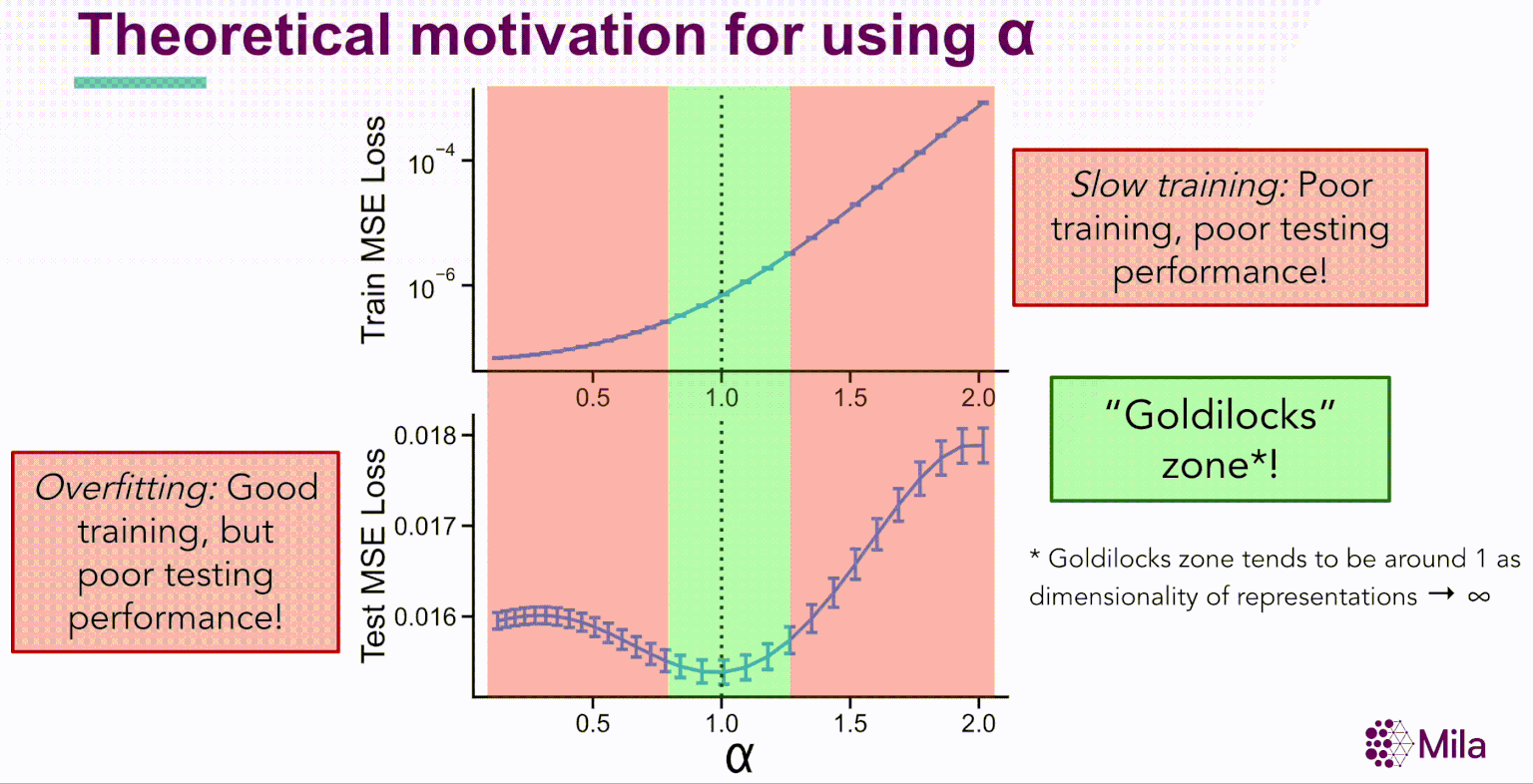
Une observation frappante immédiate de cette expérience donne à penser que les représentations intermédiaires dans les modèles profonds canoniques suivent une distribution de la loi de puissance,
λk∝k−α
où α est le coefficient de dégradation. En outre, pour les réseaux de neurones bien entraînés, α est grandement corrélé avec la généralisation dans la distribution des données d’entraînement et hors-distribution pour des ensembles de données de référence comme STL10, MIT67 et CIFAR10.
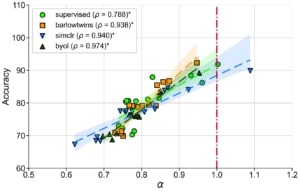
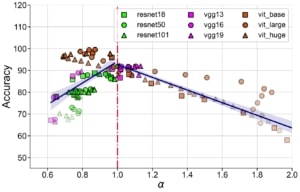
α est fortement corrélé avec la performance de reconnaissance d’objets dans STL10 pour différentes architectures et fonctions de perte de préentraînement.
Ces résultats suggèrent que le coefficient de dégradation spectrale α pourrait généralement prédire la généralisation dans les réseaux de neurones bien entraînés. Soulignons que α est une condition nécessaire (et non suffisante) dont l’évaluation est indépendante de la distribution des étiquettes et qui ne nécessite pas l’apprentissage de nouveaux modules pour évaluer la qualité de la représentation.
Cartographie du paysage de conception de la méthode Barlow Twins
Avec la preuve empirique que α constitue une bonne mesure de la généralisation, nous souhaitons maintenant étudier son adéquation en tant qu’indicateur permettant de déterminer les meilleurs modèles parmi ceux qui ont été entraînés à l’aide d’algorithmes d’AAS. Un indicateur sans étiquette comme α pourrait être utile lorsque nous n’avons pas accès aux annotations des tâches en aval et lorsque la perte associée à l’AAS est insuffisante pour distinguer les modèles présentant de bonnes capacités de généralisation (voir ci-dessous). Pour examiner cela, nous étudions la relation entre α et la performance du modèle dans une large gamme d’hyperparamètres pour un algorithme d’AAS non contrastif représentatif.
En particulier, l’objectif d’apprentissage de la méthode Barlow Twins propose d’imposer une contrainte de blanchiment doux:

dans lequel d (dimensionnalité de la tête du projecteur) et λ (coefficient de réduction de la redondance) sont des hyperparamètres clés. Par ailleurs, nos résultats suggèrent que, contrairement à la perte associée à l’AAS, le coefficient de dégradation (α) est fortement corrélé à la généralisation en aval dans une large gamme de (d,λ).
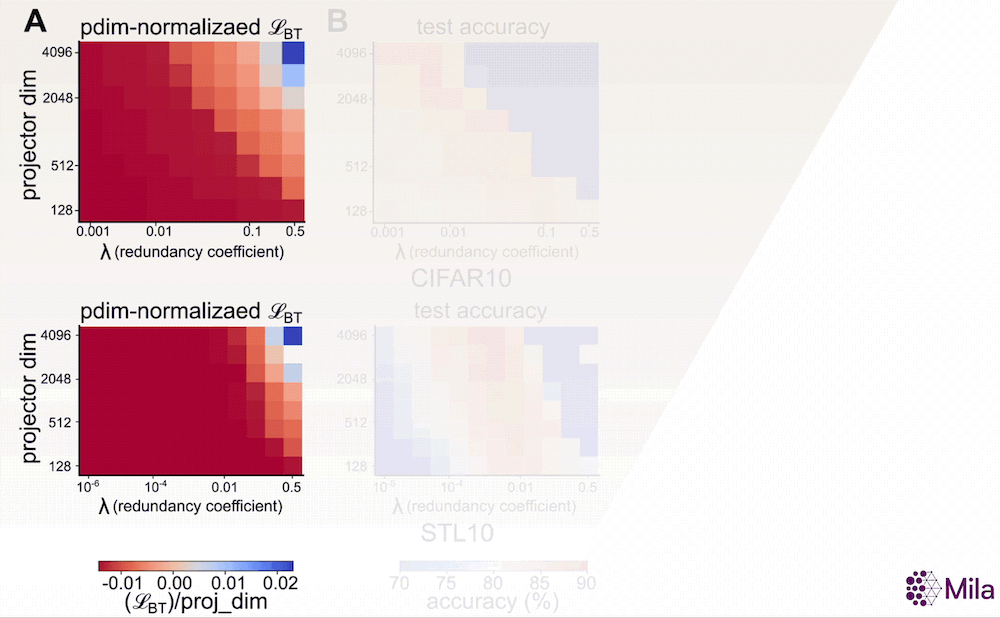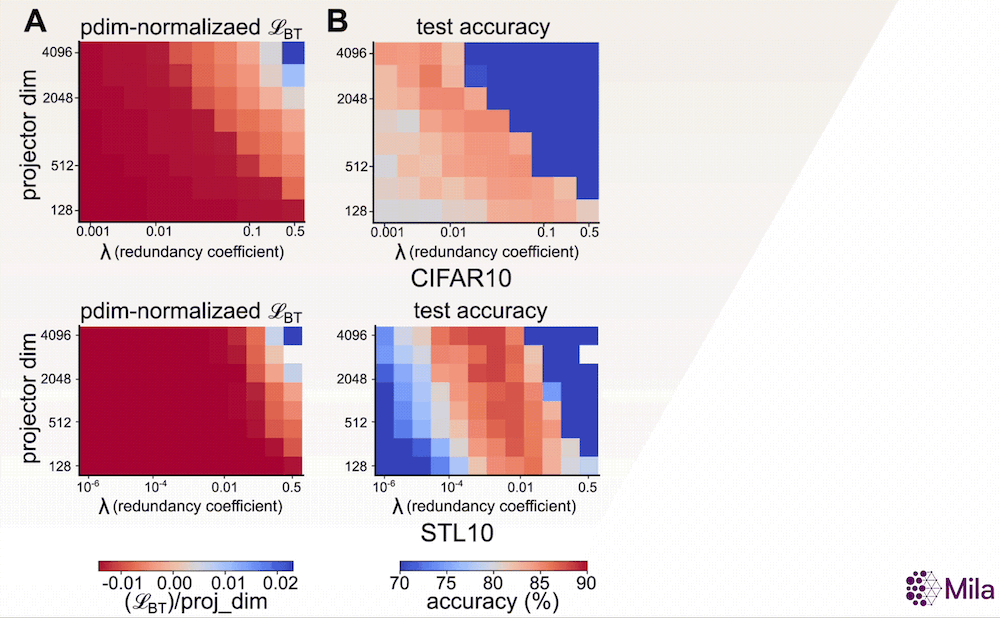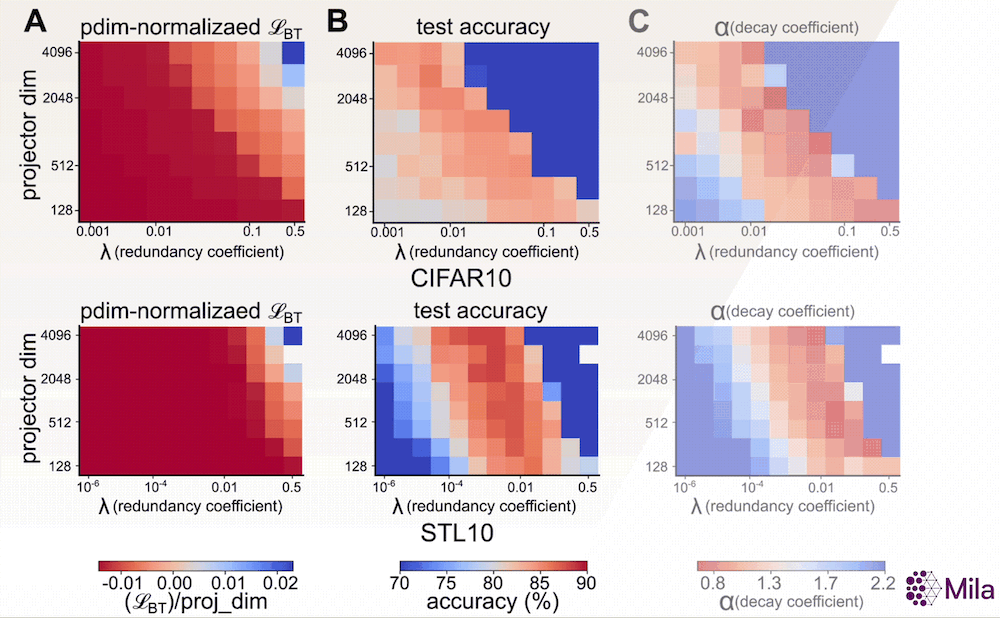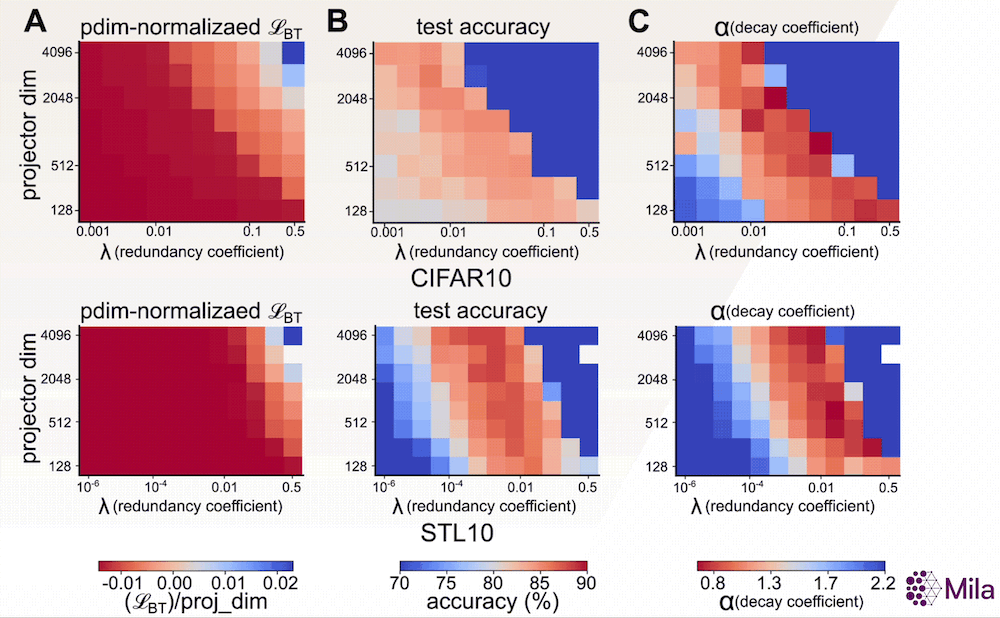
La perte associée à l’AAS (fixation du nombre de pas de gradient) n’est plus utile pour distinguer les modèles dont les performances en aval sont supérieures. Cependant, le coefficient de dégradation α est fortement corrélé à la précision du test en aval pour une large gamme d’hyperparamètres. Mesure de la généralisation dans la distribution pour la méthode Barlow Twins (A-C) entraînée et évaluée sur CIFAR10 et la méthode Barlow Twins (D-F) entraînée et évaluée sur STL10.
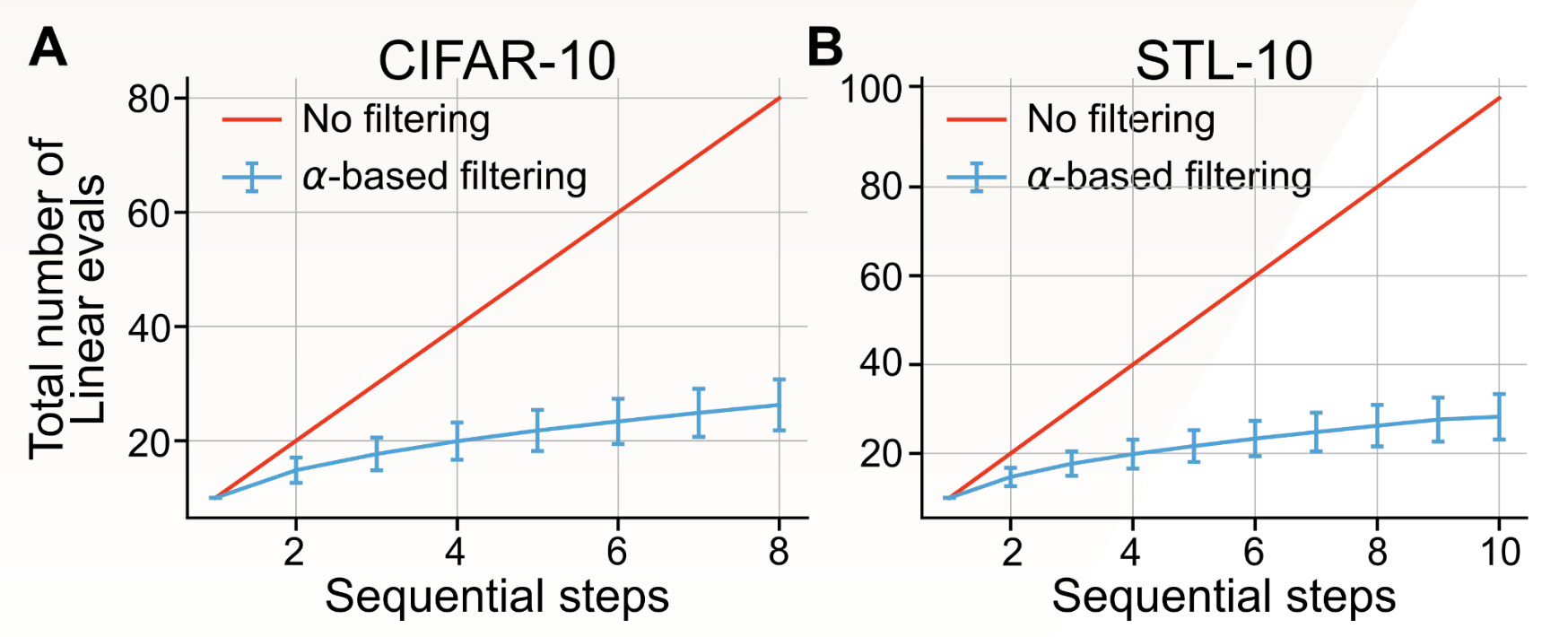
Sélection de modèle avec un budget de calcul
L’apprentissage de représentations fiables sous contrainte de ressources peut démocratiser et accélérer le développement de systèmes d’intelligence artificielle. Pour étudier cela, nous envisageons la tâche de sélection de modèle avec un budget de calcul fixe. Prenons un scénario dans lequel nous disposons d’un budget fixe pour sélectionner le modèle le plus facile à généraliser à partir d’un ensemble de modèles préentraînés comportant différents hyperparamètres. En particulier, nous considérons le cadre dans lequel nous pouvons entraîner des modèles M en parallèle et effectuer des étapes séquentielles H pour évaluer des modèles M×H.
Le protocole d’évaluation linéaire standard nous obligerait à entraîner les modèles M×H. Cependant, en se servant de α comme condition nécessaire, mais insuffisante, pour la généralisation, nous pouvons réduire le nombre de modèles à évaluer à M×log(H). L’idée critique consiste à utiliser α pour déterminer la zone idéale, où le modèle n’est ni redondant ni effondré, ainsi qu’à effectuer une évaluation linéaire uniquement pour ce sous-ensemble de modèles.
Problèmes ouverts
Des mesures efficaces de la qualité de la représentation apprises grâce à l’AAS et qui se généralisent bien à une série de tâches en aval en sont encore à leurs balbutiements. Dans cette étude, nous déterminons que le coefficient de dégradation du spectre propre α est une statistique simple permettant de classer approximativement les modèles en vue d’une bonne généralisation hors distribution.
De tels indicateurs pourraient également servir de substituts pour la recherche automatique d’architectures de neurones. Par exemple, l’estimation de α sur l’intégration des attributs pour les architectures de transformeurs révèle un rang effectif inférieur. Toutefois, une compréhension rigoureuse de cet écart caractéristique par rapport aux homologues convolutifs constitue un problème ouvert difficile à résoudre.
D’autres questions naturelles se posent, dont : Comment concevoir des objectifs d’apprentissage qui optimisent implicitement ou explicitement ces indicateurs pendant l’entraînement? Bien qu’il s’agisse de problèmes passionnants, nous espérons que notre enquête préliminaire suscitera l’intérêt de la communauté pour la poursuite d’une approche fondée sur des principes en matière de conception de modèles de réseaux de neurones.
Références
- Self-supervised learning: The dark matter of intelligence, Lecun & Misra 2021
- Advancing Self-Supervised and Semi-Supervised Learning with SimCLR, Chen & Hinton 2020
- Understanding self-supervised Learning Dynamics without Contrastive Pairs, Tian 2021
- Barlow Twins: Self-Supervised Learning via Redundancy Reduction, Zbontar 2021
- Distributed hierarchical processing in the primate cerebral cortex, Felleman & Essen 1991
- High-dimensional geometry of population responses in visual cortex, Stringer 2018
- Increasing neural network robustness improves match to macaque V1 eigenspectrum, spatial frequency preference and predictivity, Kong 2022
- Benign Overfitting in Linear Regression, Bartlett 2019
- Very Deep Convolutional Networks for Large-Scale Image Recognition, Simonyan 2014
- Deep Residual Learning for Image Recognition, He 2016
- An Image is Worth 16×16 Words: Transformers for Image Recognition at Scale, Dosovitsky 2020
- Bootstrap your own latent: A new approach to self-supervised Learning, Grill 2020
- Barlow Twins: Self-Supervised Learning via Redundancy Reduction, Zbontar 2021
- A Simple Framework for Contrastive Learning of Visual Representations, Chen 2020
- Evolving neural networks through augmenting topologies, Stanley 2002
- Neural Architecture Search with Reinforcement Learning, Zoph & Le 2016