Yoshua Bengio

Biography

*For media requests, please write to medias@mila.quebec.

For more information please contact Marie-Josée Beauchamp, Administrative Assistant at marie-josee.beauchamp@mila.quebec.

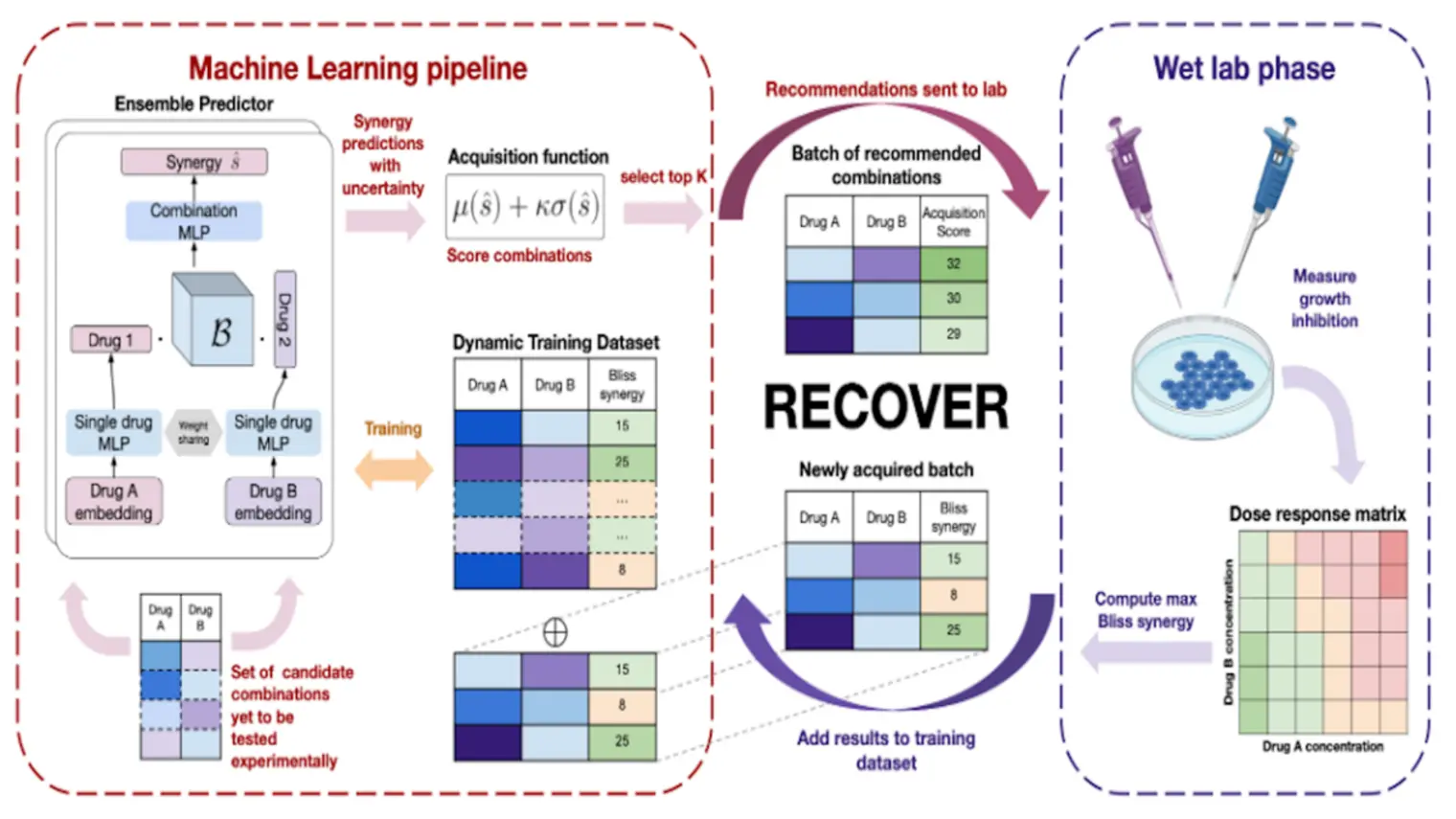
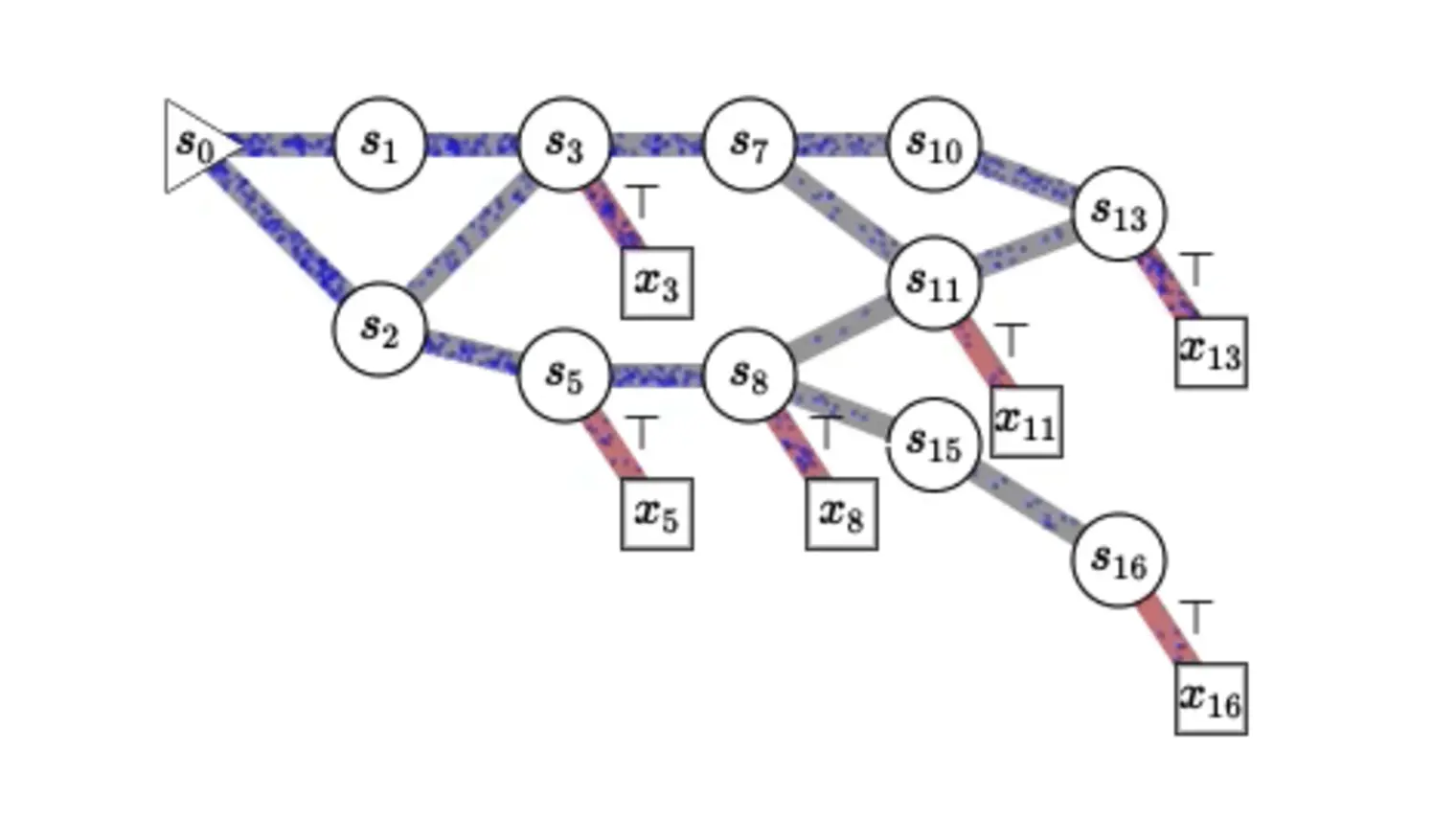
Yoshua Bengio is recognized worldwide as a leading expert in AI. He is most known for his pioneering work in deep learning, which earned him the 2018 A.M. Turing Award, “the Nobel Prize of computing,” with Geoffrey Hinton and Yann LeCun.

Bengio is a full professor at Université de Montréal, and the founder and scientific advisor of Mila – Quebec Artificial Intelligence Institute. He is also a senior fellow at CIFAR and co-directs its Learning in Machines & Brains program, serves as special advisor and founding scientific director of IVADO, and holds a Canada CIFAR AI Chair.

In 2019, Bengio was awarded the prestigious Killam Prize and in 2022, he was the most cited computer scientist in the world by h-index. He is a Fellow of the Royal Society of London, Fellow of the Royal Society of Canada, Knight of the Legion of Honor of France and Officer of the Order of Canada. In 2023, he was appointed to the UN’s Scientific Advisory Board for Independent Advice on Breakthroughs in Science and Technology.

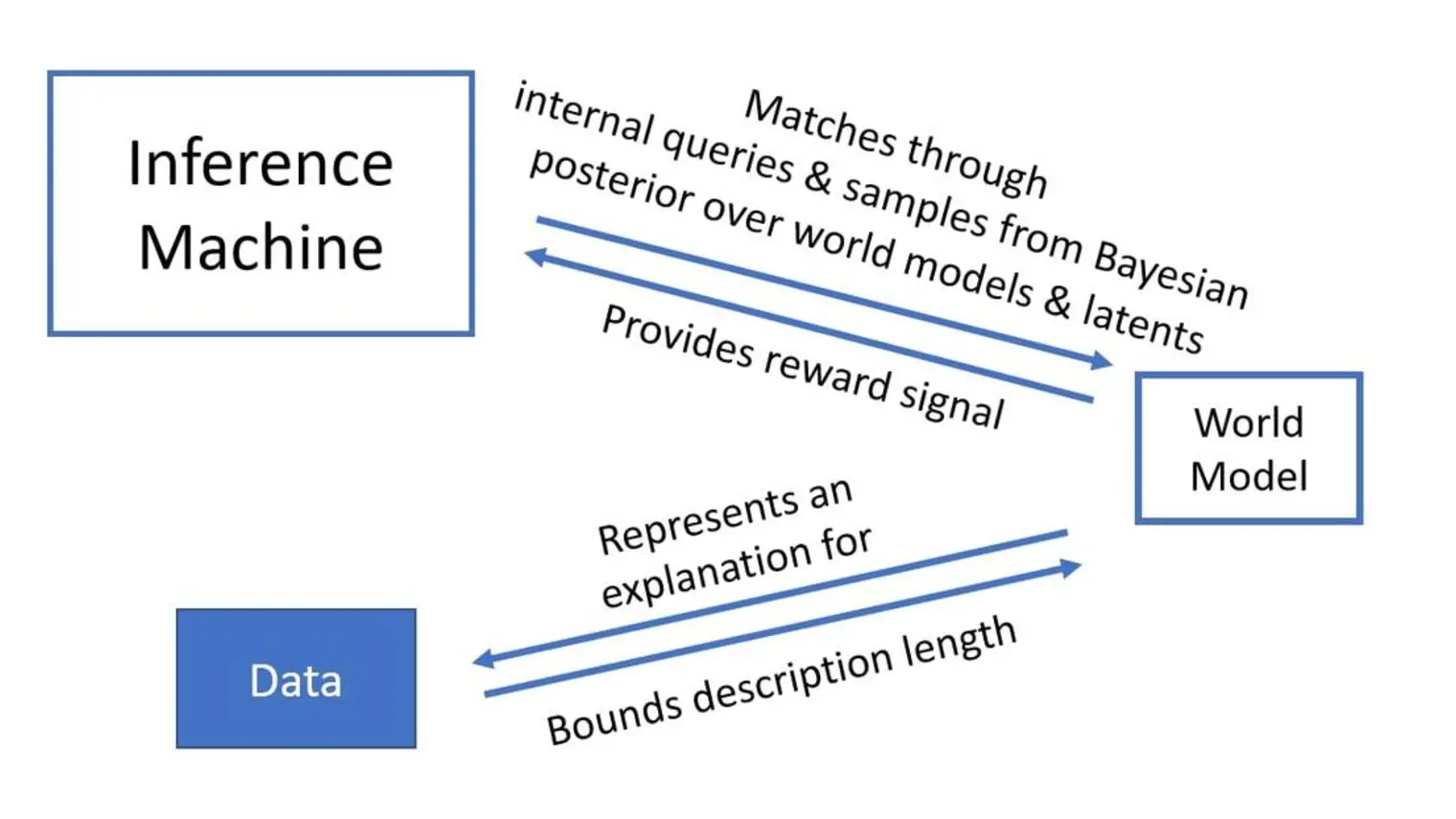
Concerned about the social impact of AI, Bengio helped draft the Montréal Declaration for the Responsible Development of Artificial Intelligence and continues to raise awareness about the importance of mitigating the potentially catastrophic risks associated with future AI systems.

Current Students

Jamal Abou Haibeh

Collaborating Alumni - McGill University

Mohammed Abukalam

Collaborating Alumni - Université de Montréal

Berkes Anaïs

Collaborating researcher - Cambridge University

Principal supervisor :

Rim Assouel

PhD - Université de Montréal

Stefan Bauer

Independent visiting researcher

Co-supervisor :

Guillaume Lajoie

Paul Bertin

PhD - Université de Montréal

Shahana Chatterjee

Collaborating researcher - N/A

Principal supervisor :

David Rolnick

Xiaoyin Chen

PhD - Université de Montréal

Sanghyeok Choi

Collaborating researcher - KAIST

Collaborating Alumni - Université de Montréal

PhD - Université de Montréal

Research Intern - Université de Montréal

Co-supervisor :

Loubna Benabbou

Eric Elmoznino

PhD - Université de Montréal

Co-supervisor :

PhD - Université de Montréal

Jean-Pierre Falet

PhD - Université de Montréal

Co-supervisor :

Leo Feng

PhD - Université de Montréal

leo.feng@mila.quebec

Ivan Grega

Research Intern - Université de Montréal

PhD

PhD - Université de Montréal

mohsin.hasan@mila.quebec

Edward Hu

PhD - Université de Montréal

Moksh Jain

PhD - Université de Montréal

moksh.jain@mila.quebec

PhD - Université de Montréal

Principal supervisor :

Collaborating Alumni - Université de Montréal

Hyeonah Kim

Postdoctorate - Université de Montréal

Principal supervisor :

Alex Hernandez

Yaroslav KIVVA

Collaborating researcher - Université de Montréal

Salem Lahlou

Collaborating Alumni - Université de Montréal

Tabitha Edith Lee

Postdoctorate - Université de Montréal

Principal supervisor :

Seanie Lee

Collaborating Alumni - Université de Montréal

Collaborating Alumni

Zhen Liu

Collaborating Alumni - Université de Montréal

Principal supervisor :

Liam Paull

Kanika Madan

PhD - Université de Montréal

Nikolay Malkin

Collaborating Alumni - Université de Montréal

Cristian Dragos Manta

PhD - Université de Montréal

Co-supervisor :

Dhanya Sridhar

Sören Mindermann

Collaborating researcher - Université de Montréal

Sarthak Mittal

PhD - Université de Montréal

Principal supervisor :

PhD - Université de Montréal

Principal supervisor :

Postdoctorate - Université de Montréal

Principal supervisor :

Independent visiting researcher - Université de Montréal

Padideh Nouri

PhD - Université de Montréal

Principal supervisor :

Ali Parviz

Collaborating researcher - Ying Wu Coll of Computing

Lena Podina

PhD - University of Waterloo

Principal supervisor :

Collaborating Alumni - Max-Planck-Institute for Intelligent Systems

Amine RAZIG

Research Intern - Université de Montréal

Co-supervisor :

Loubna Benabbou

Jarrid Rector-Brooks

PhD - Université de Montréal

Danyal REHMAN

Postdoctorate - Université de Montréal

James Requeima

Independent visiting researcher - Université de Montréal

Oli RICHARDSON

Postdoctorate - Université de Montréal

Camille Rochefort-Boulanger

PhD - Université de Montréal

Principal supervisor :

Julie Hussin

Luca Scimeca

Postdoctorate - Université de Montréal

Master's Research - Université de Montréal

Marcin Sendera

Collaborating Alumni - Université de Montréal

Postdoctorate

Marco Stock

Independent visiting researcher - Technical University of Munich

marco.stock@tum.de

Mélisande Astrid Crystal Teng

PhD - Université de Montréal

Co-supervisor :

Hugo Larochelle

alexander.tong@mila.quebec

Alex Tong

Postdoctorate - Université de Montréal

Postdoctorate - Université de Montréal

Co-supervisor :

PhD - Université de Montréal

Principal supervisor :

Collaborating researcher

Collaborating researcher - Université de Montréal

Tianyu Zhang

PhD - Université de Montréal

PhD - McGill University

Principal supervisor :

PhD - Université de Montréal

Principal supervisor :

Aaron Courville

Skipper: Combining Spatial and Temporal Abstraction for Better Generalization

Harry Zhao

Collaborating Alumni - McGill University

Principal supervisor :

Blog Posts

Generic thumbnail for Mila Blog articles.

February 22, 2024

Mingde Harry Zhao

Safa Alver

Harm van Seijen

Romain Laroche

Doina Precup

Yoshua Bengio

Scaling in the Service of Reasoning & Model-Based ML

April 4, 2023

Yoshua Bengio

Edward J. Hu

A collaboration between Mila and Relation Therapeutics to discover novel synergistic combinations of drugs in vitro

March 23, 2022

Paul Bertin

Jake P. Taylor-King

Yoshua Bengio

March 15, 2022

Generative Flow Networks

Yoshua Bengio

Publications

Sources of richness and ineffability for phenomenally conscious states

Xu Ji

Eric Elmoznino

George Deane

Axel Constant

Guillaume Dumas

Guillaume Lajoie

Jonathan Simon

Abstract Conscious states—state that there is something it is like to be in—seem both rich or full of detail and ineffable or hard to fu… (see more)lly describe or recall. The problem of ineffability, in particular, is a longstanding issue in philosophy that partly motivates the explanatory gap: the belief that consciousness cannot be reduced to underlying physical processes. Here, we provide an information theoretic dynamical systems perspective on the richness and ineffability of consciousness. In our framework, the richness of conscious experience corresponds to the amount of information in a conscious state and ineffability corresponds to the amount of information lost at different stages of processing. We describe how attractor dynamics in working memory would induce impoverished recollections of our original experiences, how the discrete symbolic nature of language is insufficient for describing the rich and high-dimensional structure of experiences, and how similarity in the cognitive function of two individuals relates to improved communicability of their experiences to each other. While our model may not settle all questions relating to the explanatory gap, it makes progress toward a fully physicalist explanation of the richness and ineffability of conscious experience—two important aspects that seem to be part of what makes qualitative character so puzzling.

2023-02-13

ArXiv (preprint)

Sources of richness and ineffability for phenomenally conscious states

Xu Ji

Eric Elmoznino

George Deane

Axel Constant

Guillaume Dumas

Guillaume Lajoie

Jonathan Simon

2023-02-13

ArXiv (preprint)

Distributional GFlowNets with Quantile Flows

Ling Pan

Ricky T. Q. Chen

Aaron Courville

Generative Flow Networks (GFlowNets) are a new family of probabilistic samplers where an agent learns a stochastic policy for generating com… (see more)plex combinatorial structure through a series of decision-making steps. Despite being inspired from reinforcement learning, the current GFlowNet framework is relatively limited in its applicability and cannot handle stochasticity in the reward function. In this work, we adopt a distributional paradigm for GFlowNets, turning each flow function into a distribution, thus providing more informative learning signals during training. By parameterizing each edge flow through their quantile functions, our proposed \textit{quantile matching} GFlowNet learning algorithm is able to learn a risk-sensitive policy, an essential component for handling scenarios with risk uncertainty. Moreover, we find that the distributional approach can achieve substantial improvement on existing benchmarks compared to prior methods due to our enhanced training algorithm, even in settings with deterministic rewards.

2023-02-11

ArXiv (preprint)

DynGFN: Towards Bayesian Inference of Gene Regulatory Networks with GFlowNets

Lazar Atanackovic

Alexander Tong

Jason Hartford

Leo J Lee

Bo Wang

One of the grand challenges of cell biology is inferring the gene regulatory network (GRN) which describes interactions between genes and th… (see more)eir products that control gene expression and cellular function. We can treat this as a causal discovery problem but with two non-standard challenges: (1) regulatory networks are inherently cyclic so we should not model a GRN as a directed acyclic graph (DAG), and (2) observations have significant measurement noise, so for typical sample sizes there will always be a large equivalence class of graphs that are likely given the data, and we want methods that capture this uncertainty. Existing methods either focus on challenge (1), identifying cyclic structure from dynamics, or on challenge (2) learning complex Bayesian posteriors over DAGs, but not both. In this paper we leverage the fact that it is possible to estimate the"velocity"of gene expression with RNA velocity techniques to develop an approach that addresses both challenges. Because we have access to velocity information, we can treat the Bayesian structure learning problem as a problem of sparse identification of a dynamical system, capturing cyclic feedback loops through time. Since our objective is to model uncertainty over discrete structures, we leverage Generative Flow Networks (GFlowNets) to estimate the posterior distribution over the combinatorial space of possible sparse dependencies. Our results indicate that our method learns posteriors that better encapsulate the distributions of cyclic structures compared to counterpart state-of-the-art Bayesian structure learning approaches.

2023-02-08

ArXiv (preprint)

Better Training of GFlowNets with Local Credit and Incomplete Trajectories

Ling Pan

Nikolay Malkin

Generative Flow Networks or GFlowNets are related to Monte-Carlo Markov chain methods (as they sample from a distribution specified by an en… (see more)ergy function), reinforcement learning (as they learn a policy to sample composed objects through a sequence of steps), generative models (as they learn to represent and sample from a distribution) and amortized variational methods (as they can be used to learn to approximate and sample from an otherwise intractable posterior, given a prior and a likelihood). They are trained to generate an object

2023-02-03

ArXiv (preprint)

E-Forcing: Improving Autoregressive Models by Treating it as an Energy-Based One

Yezhen Wang

Tong Che

Bo Li

Kaitao Song

Hengzhi Pei

Dongsheng Li

Autoregressive generative models are commonly used to solve tasks involving sequential data. They have, however, been plagued by a slew of i… (see more)nherent flaws due to the intrinsic characteristics of chain-style conditional modeling (e.g., exposure bias or lack of long-range coherence), severely limiting their ability to model distributions properly. In this paper, we propose a unique method termed E-Forcing for training autoregressive generative models that takes advantage of a well-designed energy-based learning objective. By leveraging the extra degree of freedom of the softmax operation, we are allowed to make the autoregressive model itself an energy-based model for measuring the likelihood of input without introducing any extra parameters. Furthermore, we show that with the help of E-Forcing, we can alleviate the above flaws for autoregressive models. Extensive empirical results, covering numerous benchmarks demonstrate the effectiveness of the proposed approach.

2023-02-01

ICLR.cc/2023/Conference (rejected)

openreview.net

Generative Augmented Flow Networks

Ling Pan

Aaron Courville

Longbo Huang

The Generative Flow Network is a probabilistic framework where an agent learns a stochastic policy for object generation, such that the prob… (see more)ability of generating an object is proportional to a given reward function. Its effectiveness has been shown in discovering high-quality and diverse solutions, compared to reward-maximizing reinforcement learning-based methods. Nonetheless, GFlowNets only learn from rewards of the terminal states, which can limit its applicability. Indeed, intermediate rewards play a critical role in learning, for example from intrinsic motivation to provide intermediate feedback even in particularly challenging sparse reward tasks. Inspired by this, we propose Generative Augmented Flow Networks (GAFlowNets), a novel learning framework to incorporate intermediate rewards into GFlowNets. We specify intermediate rewards by intrinsic motivation to tackle the exploration problem in sparse reward environments. GAFlowNets can leverage edge-based and state-based intrinsic rewards in a joint way to improve exploration. Based on extensive experiments on the GridWorld task, we demonstrate the effectiveness and efficiency of GAFlowNet in terms of convergence, performance, and diversity of solutions. We further show that GAFlowNet is scalable to a more complex and large-scale molecule generation domain, where it achieves consistent and significant performance improvement.

2023-02-01

ICLR.cc/2023/Conference (notable)

openreview.net

GFlowNets and variational inference

Nikolay Malkin

Salem Lahlou

Tristan Deleu

Xu Ji

Edward J Hu

Katie E Everett

This paper builds bridges between two families of probabilistic algorithms: (hierarchical) variational inference (VI), which is typically us… (see more)ed to model distributions over continuous spaces, and generative flow networks (GFlowNets), which have been used for distributions over discrete structures such as graphs. We demonstrate that, in certain cases, VI algorithms are equivalent to special cases of GFlowNets in the sense of equality of expected gradients of their learning objectives. We then point out the differences between the two families and show how these differences emerge experimentally. Notably, GFlowNets, which borrow ideas from reinforcement learning, are more amenable than VI to off-policy training without the cost of high gradient variance induced by importance sampling. We argue that this property of GFlowNets can provide advantages for capturing diversity in multimodal target distributions.

2023-02-01

ICLR.cc/2023/Conference (poster)

openreview.net

GFlowNets for AI-Driven Scientific Discovery

Moksh J. Jain

Tristan Deleu

Jason Hartford

Cheng-Hao Liu

Alex Hernandez-Garcia

Tackling the most pressing problems for humanity, such as the climate crisis and the threat of global pandemics, requires accelerating the p… (see more)ace of scientific discovery. While science has traditionally relied...

2023-02-01

ArXiv (preprint)

Improving and generalizing flow-based generative models with minibatch optimal transport

Alexander Tong

Yanlei Zhang

Kilian FATRAS

Continuous normalizing flows (CNFs) are an attractive generative modeling technique, but they have been held back by limitations in their si… (see more)mulation-based maximum likelihood training. We introduce the generalized conditional flow matching (CFM) technique, a family of simulation-free training objectives for CNFs. CFM features a stable regression objective like that used to train the stochastic flow in diffusion models but enjoys the efficient inference of deterministic flow models. In contrast to both diffusion models and prior CNF training algorithms, CFM does not require the source distribution to be Gaussian or require evaluation of its density. A variant of our objective is optimal transport CFM (OT-CFM), which creates simpler flows that are more stable to train and lead to faster inference, as evaluated in our experiments. Furthermore, we show that when the true OT plan is available, our OT-CFM method approximates dynamic OT. Training CNFs with CFM improves results on a variety of conditional and unconditional generation tasks, such as inferring single cell dynamics, unsupervised image translation, and Schr\"odinger bridge inference.

2023-02-01

ArXiv (preprint)