This blog post is co-written by my PhD student Edward J. Hu.
Scaling seems to work really well.
We must be cautious in pursuing research directions that build knowledge directly into AI systems at the expense of scalability. In fact, even nature builds intelligence on top of large-scale biological neural networks.
However, current large-scale systems still exhibit significant factual errors and unpredictable behavior when deployed. While these errors might improve with short-term solutions like more filters, better retrievers, and smarter prompts, these systems do not think like humans do, as indicated by cognitive neuroscience, in particular, the global workspace theory [Baar, 1988] and its descendants. It is hard to entrust such a system, of which we have little understanding, with important tasks.
In our opinion, further scaling is unlikely to resolve these reliability issues. The Inverse Scaling Prize shows that larger models actually do worse on many well-specified tasks. If we were to believe that larger models would be necessarily more reliable, any sign of “inverse” scaling should be alarming. Many of these tasks involve forms of reasoning, suggesting that, to achieve human-level robust reasoning, we need additional inductive biases.
This blog post describes long-term research directions that leverage both inductive biases and scaling. We will highlight what is, in our opinion, the source of the problem with the current state-of-the-art and delineate potential solutions. First, we need to discuss: what is reasoning?
Reasoning = Knowledge + Inference
Reasoning, or thinking, is the process of asking and answering questions using a source of knowledge.
Human reasoning involves generating a small number of intermediate steps, i.e., thoughts, each of which combines very few pieces of knowledge in a coherent way [Baar, 1988]. The broad technical term in probabilistic machine learning for “answering questions” is inference. Formally, we take inference to mean finding modes of the conditional distribution P(solution | query, knowledge). A “solution” or answer to the question here can take the form of an arbitrary compositional object. It can include both the explicit answer to the query and hypothesized explanations about the link between query and answer. Natural language sequences are usually a reflection of such compositional objects, like semantic parse trees, that are in our minds when an answer pops up, and are part of the explanation for the sentence, helping us to answer a question about it. As argued below, to reason well, we need to have 1) a good model of the world and 2) a powerful inference machine to generate solutions compatible with the world model.
This is where different end goals and computational vs statistical trade-offs appear.
On one hand, per Occam’s razor, our world model looks for minimally sufficient pieces of knowledge to explain the observed data. It should be compact in terms of how many bits it encodes and maximize the reusability of knowledge pieces so it can generalize well to unseen situations. For example, in the game of Go, the world model should capture the few rules of the game from gameplays, so it can explain previously unseen gameplays. This world model is not restricted to be in an explicit form, like a knowledge graph. It might take the form of an energy-based model E(query, solution) parametrized by a neural network that evaluates the compatibility between a query and a solution, and possibly more formal and verbalizable knowledge of the kind we use in science, math, databases, or wikipedia. Nonetheless, the effective capacity of this neural network is bottlenecked by the amount of data we have – a larger neural network can easily overfit if its parameters are fully exploited.
On the other hand, a trained inference machine can amortize search in a large solution space; it learns to quickly provide answers that are good and that an expensive run-time search method (like MCMC, classical AI, or optimization methods) may otherwise provide. It must be very powerful – exact inference, which exhausts all combinatorial configurations of knowledge pieces, generally becomes intractable even with a modest amount of knowledge. Consider how a few very simple rules, like in the game of Go, call for a very large neural network in order to perform good inference, i.e., play at the champion-level. In other words, approximate inference is where scaling shines: the larger the model, the better the approximation. However, a large neural net comes with a price in terms of the number of examples needed to feed the beast and ensure its accuracy.
When it comes to robust reasoning, an Achilles’ heel of current large language models is that the world model and the inference machine are one and the same. A monolithic neural network trained end-to-end on the given training data to perform the desired inference might have a hard time achieving both end goals at the same time. A powerful inference machine that directly encapsulates knowledge can easily result in an overcomplicated, albeit implicit, world model. Seen in this light, It’s less surprising that current large language models sometimes fail to generalize to new observations the same way humans do.
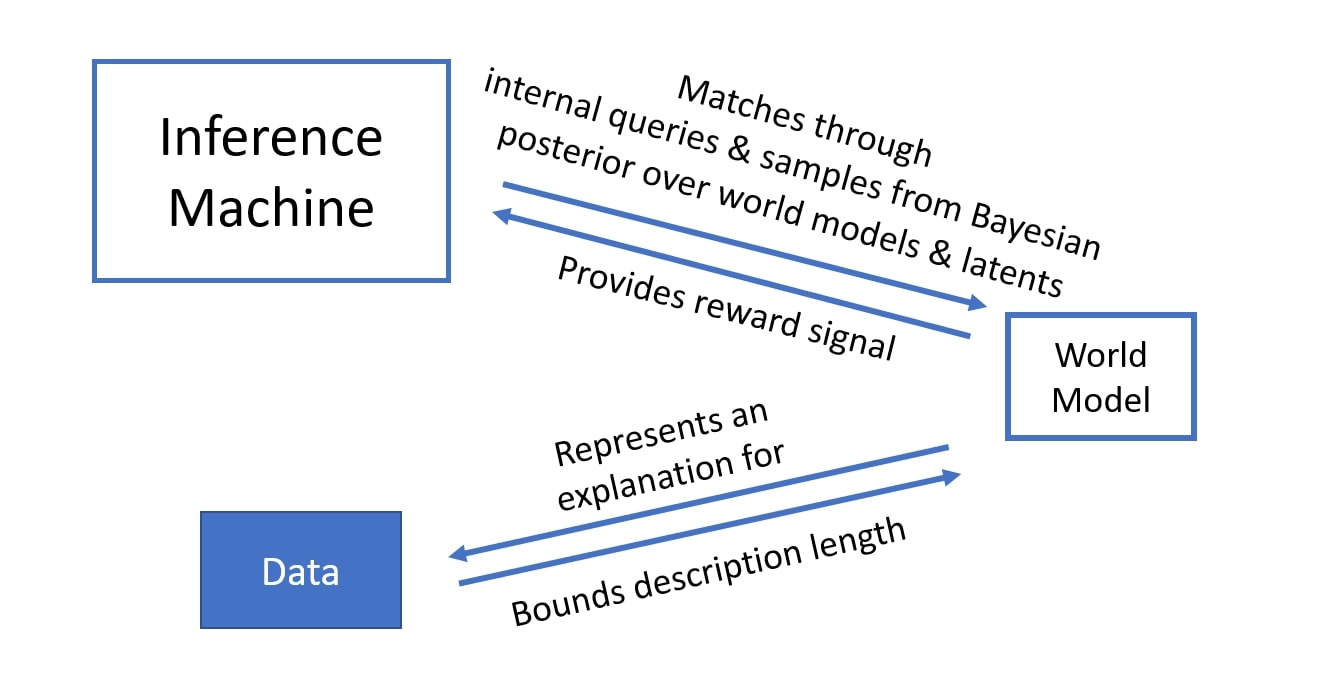
The rest of the blog post delineates what an ideal world model and an ideal inference machine may look like. We start with the properties of an ideal world model.
The ideal world model
Humans’ mental model of the world allows us to quickly generalize to new situations using very little new data, such as driving on the opposite side of the road due to a modified traffic law or solving novel coding puzzles.
We do so by reusing and adapting existing pieces of knowledge, analogous to the principles of modularity and reusability in programming. We also rely on natural languages and other abstract symbols to organize knowledge and thoughts and to communicate them in compact forms, e.g., with equations or dictionary definitions. In fact, our working memory is so limited in its capacity that it can only hold a small discrete set of concepts [Dehaene et al., 2022]. This biological bottleneck, at the heart of the Global Workspace Theory [Baar, 1988] from cognitive neuroscience, forces a compact and modular world model [Goyal & Bengio 2022]. There is in fact evidence from neuroscience that our working memory compresses the observed information by exploiting its abstract structure (such as repetitions), similarly to how defining a new concept allows to use it in a way that requires less bits in total if the concept is reused several times, and this capability may be connected to why we invent new abstractions in ways that differ from other animals [Dehaene et al., 2022]. With the help of natural languages, we keep inventing new abstractions and definitions to better compress and make sense of the world.
In addition to modularity, the notion of uncertainty is crucial. With finite data, there are generally many world models that can fit it. Relying on a single model may yield inference results that are confidently wrong, e.g., unsafe decisions. Instead, humans are able to assess their own level of uncrtainty about a statement, if only coarsely, and thus handle risks more appropriately. Knowing one’s own uncertainty about one’s knowledge is also crucial to efficient knowledge acquisition [Jain et al 2023]. For example, we can gather more training data for scenarios with high uncertainty or using good uncertainty estimates is even allowing us to start automating experimental design in scientific research.
Finally, the world model should take advantage of the out-of-distribution generalization power afforded by modeling causal relationships. Causality plays an important role in human reasoning. For example, we know that gravity causes things to fall and rain causes roads to be wet – but not the other way around, because making the ground wet does not make rain happen. A causal model can be understood as an exponentially large family of distributions indexed by a choice of intervention, where an intervention sets or changes some variables. In the case of human reasoning, it is often the action of an agent. Such causal knowledge helps us to generalize to an unseen distribution corresponding to an unseen intervention. It also helps us decide how to intervene in the world to achieve our desired goals as well as reason counterfactually by answering “what could have happened had I done it differently,” a likely tool for abstract credit assignments that can be effective for learning long-term causal dependencies [Kemp et al., 2015].
Model-Based Machine Learning with Large Deep Nets as Amortized Inference Machines
To think is to search for ideas or solutions.
Inference is about finding needles in a haystack. The distribution P(solution | query, knowledge) typically favors a tiny number of modes (regions of high probability in solution-space) out of an exponentially large space of possible solutions. Classical inference, including Markov Chain Monte Carlo (MCMC), is based on brute-force search: trying a large number of solutions, often by improving on previously found ones. This is very expensive at run-time and not practical from the point of view of an animal facing immediate danger. Instead, the computational cost of inference can be amortized, meaning it trades a computationally expensive training procedure for fast inference – the inference machine gets better the more it gets used and fine-tuned. For example, a scientist might practice problem-solving in school for two decades while gradually becoming much faster at answering hard questions in her area. An unamortized approach would mean no schooling but instead finding answers from scratch for every question; it won’t scale to hard problems. This rules out simulation-based inference such as MCMC as well as classical AI search methods like A*. Meanwhile, this AI education, obtained by amortized learning, should be amenable to efficient stochastic gradient-based optimization to take advantage of the advances in deep learning of the last two decades.
What we propose is to rekindle an old idea in science and ML: separate the world model and the inference machine, but exploit modern deep learning to train a very large amortized inference machine. How should it be trained? The amortized inference machine should be consistent with the world model. If one is asked “how can I make fluffy brioche?”, the answer should be based on the relevant pieces of knowledge about baking, combined in a coherent way. This consistency can be encouraged by a training procedure that queries the world model and quantifies how consistent the result of inference is with all the relevant pieces of knowledge. An added benefit is that if we can afford lots of computations used to train the inference machine with queries to the world model, we will not easily overfit even if the amortized inference machine is very large. There are combinatorially many questions that can be asked and used to train the amortized inference machine: the amount of “fake” examples used to train the inference machine is now unbounded because these “fake examples” are not limited by real data but instead arise as internal queries, the number of which is only limited by our computational capability. Consequently, we can fully leverage the power of large neural networks for the inference machine, without fear of them overfitting.
In addition, there is often more than one solution to a query. The inference machine should be able to model a multimodal distribution over answers, instead of a point estimate, that are compatible with the world model and the query. This goes hand-in-hand with the notion of uncertainty in the world model – we often have multiple hypotheses of how the world works. In fact, the same probabilistic inference machinery can, in a Bayesian way, predict what the world model should really be [Deleu et al., UAI’22]. Then, areas of high uncertainty can be made less uncertain through the acquisition of relevant data [Jain et al., 2023].
Finally, the inference machine must efficiently explore the large solution space. To represent the combinatorially many candidates in the solution space, the inference machine can generate a solution through a sequence of stochastic steps, each chosen from a much smaller action space. For example, we can build molecules by repeatedly picking a location and adding one atom at a time. Each action is taken from a limited set but their composition through several steps makes it possible to represent an arbitrarily rich distribution over molecules. When trained on diverse queries and solutions, the inference machine can “mix and match” steps it has seen and make educated guesses to reach previously unseen solutions, e.g., by recombining functional groups to form new organic molecules. This form of generalization by exploiting the underlying regularities in the solution space is at the heart of the success of modern deep learning.
Beyond Scaling
According to Daniel Kahneman, our brain consists of System 1, characterized by fast and associative thinking, and System 2, characterized by slow and deliberate thinking. Many liken deep-learning-based language models to System 1 and postulate that a future System 2 architecture will handle robust reasoning [Goyal & Bengio 2022]. However, a standalone System 2 neural network might not be practical, for the same reason that classical symbolic AI failed – it needs to also have a powerful inference machine, for both fast inference to answer a new question on-the-fly as well as to train the world model itself and infer explanations for observed data. Indeed, our brain is full of locally dense neural networks, à la System 1, and System 2 might simply organize the computation and training of the former to achieve consistency between a powerful, amortized inference machine and an implicitly represented but compact and modular world model.
What are some credible ways to go beyond scaling current large language models?
In the short term, we might somehow encourage the world model in language models to be modular and to model uncertainty and causality; this requires more research on understanding the working of language models and how their machinery could be put to use to generate not just external actions but also an inner voice that can be seen as a latent variable that partially explains previous or upcoming external sequences of words.
In the long term, we should separate the world model and the inference machine and learn them simultaneously. This has been the goal of our lab at Mila. We built a novel probabilistic framework, called generative flow networks (GFlowNets), for amortized inference of multimodal distributions over compositional objects. GFlowNets use ideas from both variational inference and reinforcement learning to model compositional objects incrementally and probabilistically [Malkin et al., 2023].
It has found applications in
- handling uncertainty and biases in the reward signal as well as combinatorially large search spaces, such as in drug discovery [Bengio et al., 2022; Jain et al., 2022] and in the scheduling of computation graphs [Zhang et al., 2023].
- modeling the Bayesian posterior distribution over causal graphs that explain both observational and interventional data [Deleu et al., UAI’22].
- extending machine learning algorithms by sampling approximately from intractable distributions over compositional objects. For example, learning expressive latent variable models, under which a world model is a special case, using a modified expectation-maximization algorithm [Hu et al., 2023].
If you are interested in learning more about GFlowNets and how they can expand the frontier of deep learning, you can check out this tutorial.
Acknowledgements
We thank Jacob Buckman, Chen Sun, Mo Tiwari, Donna Vakalis, and Greg Yang for helpful feedback.