Generalized Data Weighting via Class-level Gradient Manipulation

Editor’s Note: Based on work published at NeurIPS 2021.

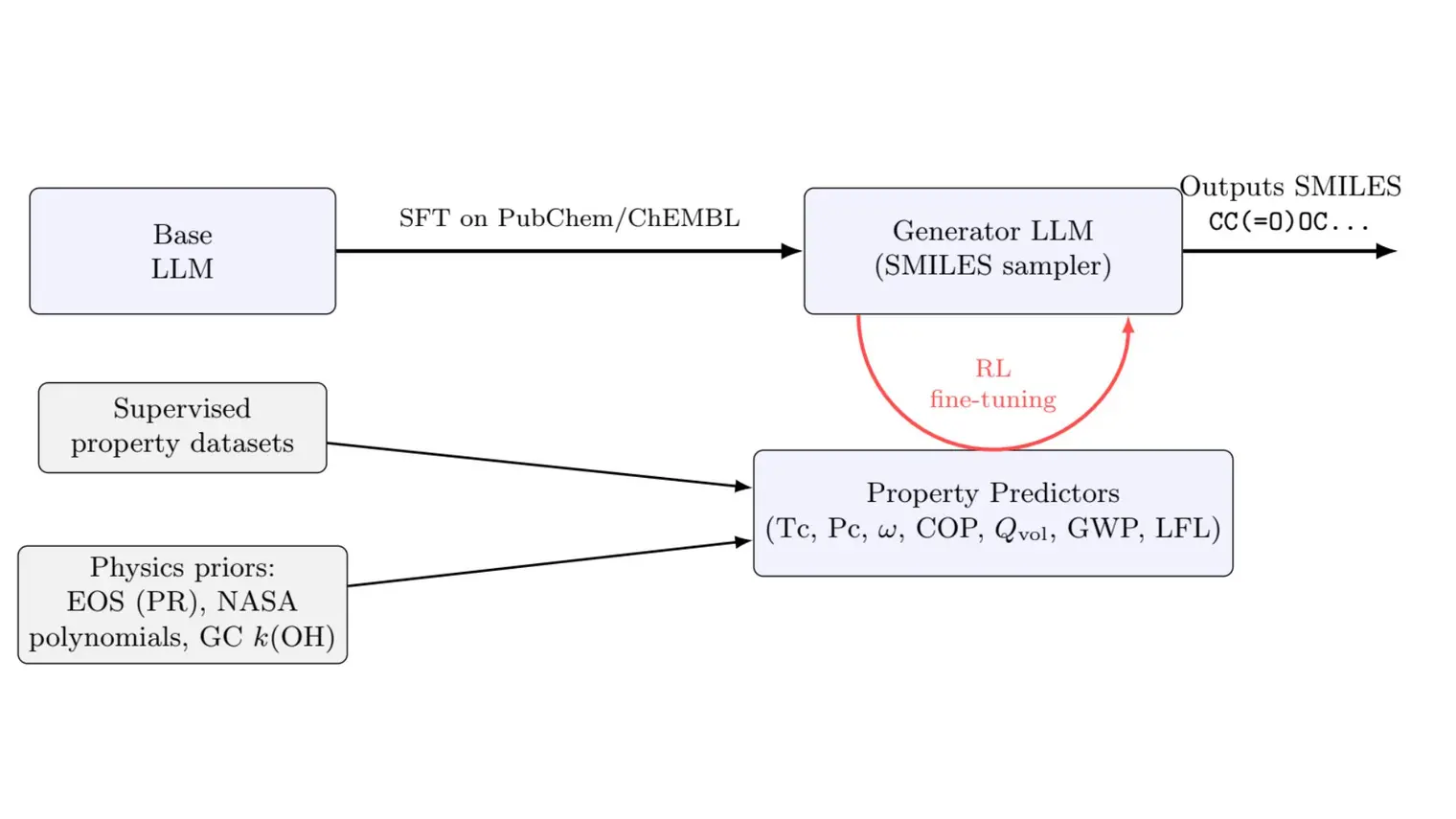
Background

Real-world classification tasks suffer from two common problems: label noise and class imbalance. For example, “cat” is mislabeled as “dog” (label noise) and the number of “cat” in the training set is much smaller than that of “dog” (class imbalance). The two problems will mislead the model training and make the model believe the ‘cat’ image is ‘dog’/there are much more ‘dog’ than ‘cat’ in the real world, which harms the model performance.

GDW: from Instance Weighting to Class-level Weighting

Previous state-of-the-art work adopted instance weighting (an instance means an image-label pair) to solve the two problems, and expected small weights for noisy instances /major classes to rebalance the data distribution. Yet, in instance weighting methods, class-level information within instances is overlooked as illustrated below.

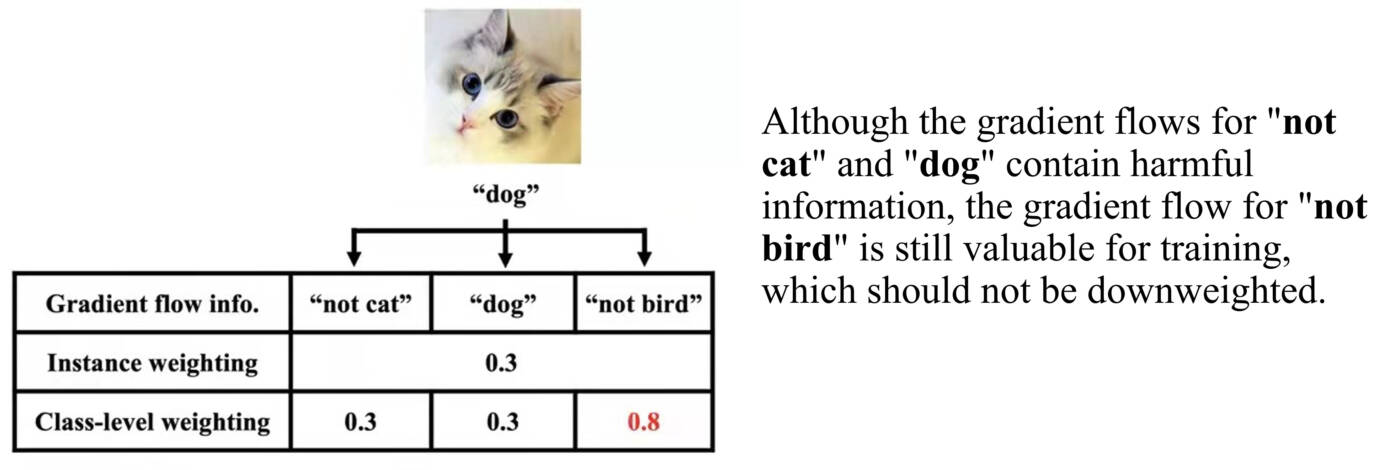
This is a three-class classification task and every instance has three logits. As shown in the above figure, there are three kinds of information: “not cat”, “dog”, and “not bird”.  Instance weighting methods alleviate label noise by discarding all three kinds of information simultaneously. Yet, discarding the “not bird” is a waste of useful information. Similarly, in class imbalance scenarios, utilizing different class-level information will improve model training. Therefore, it is necessary to reweight instances at the class level for better information usage. 

To this end, we propose Generalized Data Weighting GDW to tackle label noise and class imbalance by class-level information manipulation. We will use the above label noise case as an example. Our proposed GDW can reweight class-level information and thus makes better use of the information. GDW consists of the following steps: 

1. We introduce three class-level weights initiated as 0.5 to represent the importance of three kinds of information: “not cat”, “dog”, and “not bird”. This is achieved by unrolling the chain rule. 
2. Now the question is how to determine a good set of class-level weights. In machine learning, we generally maintain a validation set apart from the training set and we can choose some hyperparameters like learning rate based on the validation performance.
3. If we train the model with good class-level weights, we can expect the model to perform well on a validation set and yield good validation performance. We can treat these class-level weights as hyperparameters and tune them based on the validation performance. 
4. In the above process, assume the class-level weights the original class-level weights for “not cat”, “dog”, and “not bird” are 0.5, 0.5 and 0.5. The “not cat” and “dog” information are wrong and thus deserve small weights like 0.3 while the “not bird” information is correct and thus deserves a larger weight like 0.8. 
5. We will find if we train a model with the class-level weights 0.3, 0.3 and 0.8 for this image, we can obtain a better model, which performs better on the validation set. As a result, we will choose 0.3, 0.3 and 0.8 as the class-level weights.
6. The above process formulates as a bi-level optimization problem in the original paper and you can read it for further details. With the updated class-level weights, we can mitigate the label noise effect of the image to train a better model.

 In this way, GDW achieves impressive performance improvement in various settings since GDW can make use of the ‘not bird’ information, which was discarded in previous work.

Experimental Results

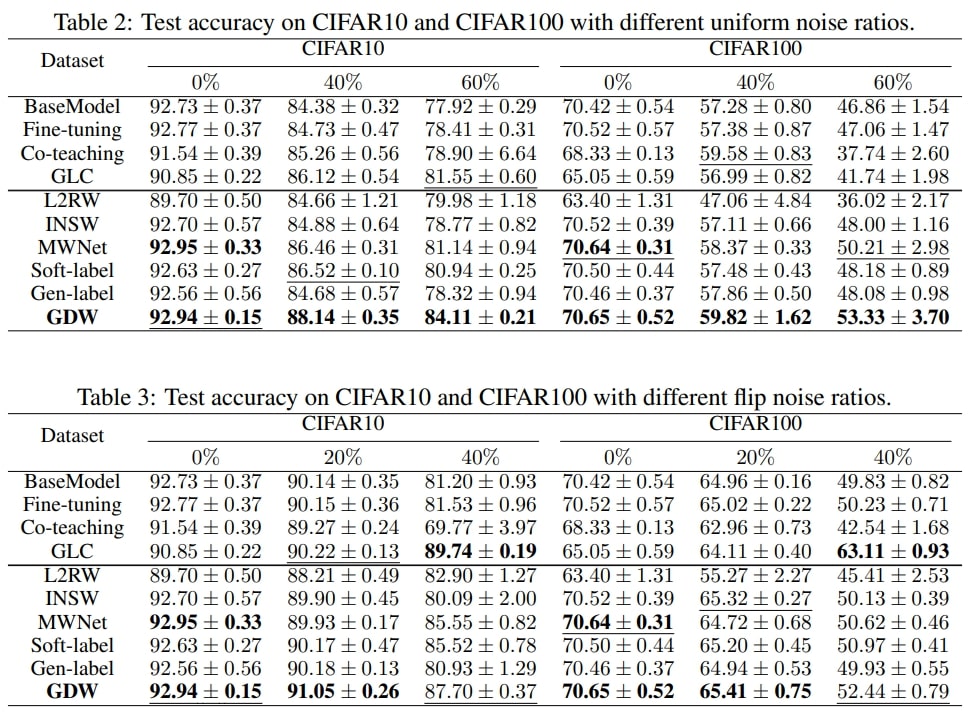
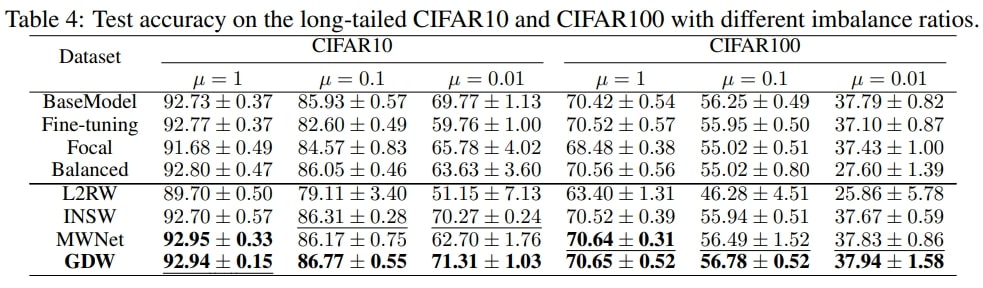
We conduct experiments on label noise settings as reported in Table 2 and Table 3, and class imbalance settings as reported in Table 4 to verify the effectiveness of our method. The evaluation metric/reported number in the three tables is the mean classification accuracy and we report the mean and standard deviation over 5 runs. The column in Table2/Table3 represents the noise ratio. For example, 20% indicates that 20% of images are noisy. The difference between the two tables is that: Table 2 randomly changes the image’s label (uniform noise) with a probability (e.g, 20%) while Table 3 flips the image’s label (e.g. cat) to another label (e.g. dog) with a certain probability (e.g, 20%). The column in Table 4 indicates the imbalance ratio. A ratio of 1 indicates that all classes in this dataset have the same number of images while a ratio of 0.01 indicates that the number of the major class is 1/0.01 = 100 times as that of the minor class.

We have the following main observations:

1. First, we can observe that GDW outperforms nearly all the competing methods in all noise settings. This verifies the effectiveness of GDW.
2. Besides, under all noise settings, GDW has a consistent performance gain compared with MWNet, which aligns with our motivation of class-level weighting over instance-level weighting.  Unlike instance-level weighting which discards all information, class-level weighting will upweight the “not bird” gradient flow, which improves the model training.
3. Furthermore, as the ratio increases in the uniform noise setting, the gap between GDW and MWNet increases also a lot in CIFAR10 and CIFAR100. Even under the extreme uniform noise, GDW still has low test errors in both datasets and obtain expressive performance gains compared with the second-best method. This proves the generalizability of GDW.
4. Last but not least, GDW performs best in nearly all imbalance settings. This proves GDW can handle class imbalance well.

Conclusion

Many instance weighting methods have recently been proposed to tackle label noise and class imbalance, but they cannot capture class-level information. These methods discard the useful class-level information: not bird in the above example. For better information use when handling the two issues, we propose GDW to generalize data weighting from instance level to class level. In this way, GDW achieves remarkable performance improvement in various settings.

Authors of the the original paper

Can Chen, Shuhao Zheng, Xi Chen, Erqun Dong, Xue (Steve) Liu, Hao Liu, Dejing Dou