Abstract
To understand this blog, we expect the reader to be familiar with recurrent neural networks and gradient descent learning via BPTT. Developing biologically-plausible learning rules is of interest for both answering neuroscience questions on how the brain learns and searching for more efficient training strategies for artificial neural networks. However, generalization properties of solutions found by these rules are severely underexamined. In this work, we brought a key theoretical ML optimization concept (loss landscape curvature) to study the generalization properties of biological learning systems. We first demonstrated empirically that existing biologically-plausible temporal credit assignment rules achieve worse generalization performance compared to their deep learning counterpart. We then derived a theorem, based on loss landscape curvature, to explain the underlying cause for this phenomenon. Finally, we suggested potential remedies that could be used by the brain to mitigate this effect. This work was presented at NeurIPS 2022.
Paper authors: Yuhan Helena Liu, Arna Ghosh, Blake Aaron Richards, Eric Shea-Brown, Guillaume Lajoie
Introduction
What is temporal credit assignment and how is it solved in artificial and biological recurrent neural networks?
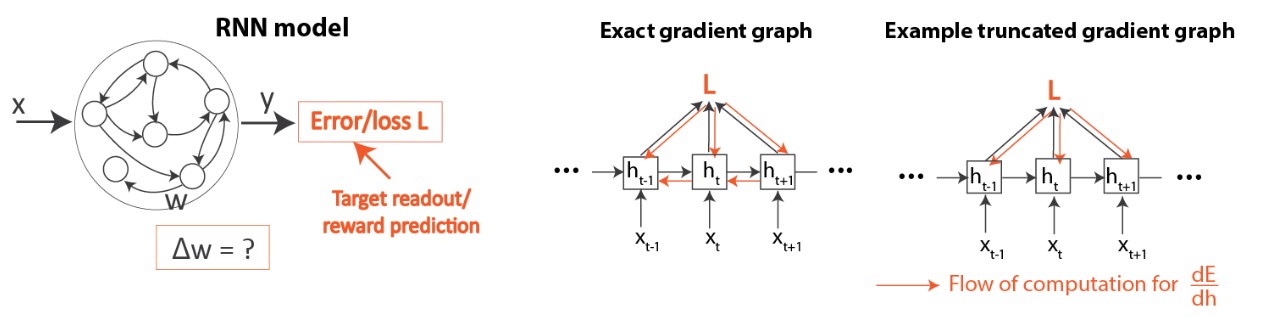
We focus on recurrent neural networks (RNNs) because it has been widely used for modeling the brain. RNNs can be trained by adjusting parameters (typically connection weights, W, between units) to learn the target input/output patterns for a computational task. How close the network is to the target can be quantified by a loss function L.
In RNNs, adjusting weights to reduce this loss function L involves solving the underlying temporal credit assignment problem: reliably assigning credit (or blame) to each weight by determining the contribution of all past neural states for error observed in the present time. For instance, suppose you are playing baseball and you saw you hit the ball incorrectly, which of your 100 trillion synapses are to blame?
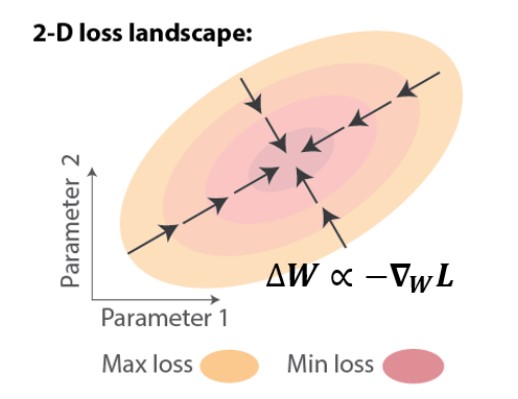
In artificial RNNs, the temporal credit assignment problem can be solved using backpropagation through time (BPTT), which applies chain rule to compute the exact gradient of the loss with respect to the weights, ∇WL. One can then perform gradient descent learning, leading to iterative improvements, i.e. loss reduction (Figure 1).
In biological networks, however, it is elusive how the temporal credit assignment problem can be solved. Due to the stunning success of training artificial neural networks, computational neuroscientists have pursued a normative approach and turned to BPTT for inspiration. The issue with that approach is that BPTT is not biologically-plausible, as explained below.
What is biological plausibility and why should we care?
Biologically-plausible means that no known biological constraints are violated. What is known is that the brain solves the temporal credit assignment using a local learning rule: every synapse adjusts its strength using only information that is physically available to it, including the activity of the two neurons connected by the synapses and any neuromodulatory signals reflecting rewards and errors. Thus, BPTT is not biologically-plausible because it demands expensive nonlocal information inaccessible to neural circuits [1]: in order to use the chain rule, it would require artificial neurons to constantly track the synaptic activity of all neurons in the network. Elucidating how local rules can lead to successful temporal credit assignment would not only advance our understanding of how the brain learns, but could also lead to more energy-efficient learning on neuromorphic chips that avoid communication overheads of BPTT.
What are existing biologically-plausible temporal credit assignment algorithms? How well do they perform?
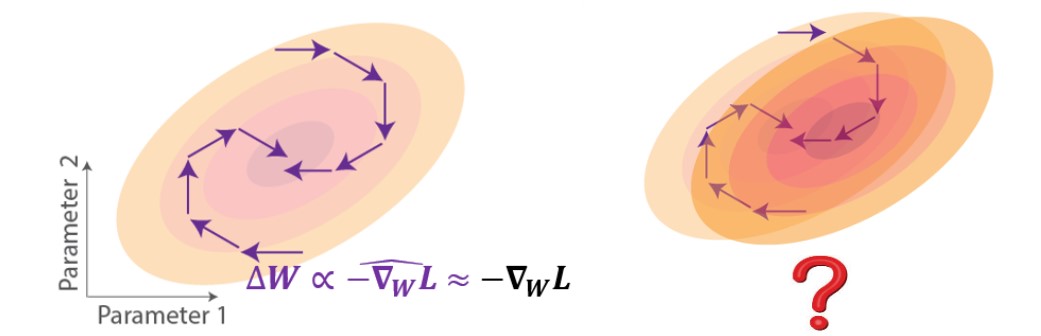
The most successful approaches to implementing biologically-plausible temporal credit assignment mechanisms have been based on approximating gradients [2-5]. These approaches focus on truncating the exact gradient to obey the locality constraint. Geometrically on the loss landscape, weight updates using approximate gradient descent learning would point in a direction that partially follows the gradient, which could still lead to loss reduction if they have a positive component in the gradient direction (Figure 2, left). Despite the ability of these approximate rules to approach the task objective, little is known about how they would impact generalization (Figure 2, right). For instance, if we test with perturbed data reflected as a shift in the loss landscape, how would the network trained under such rules perform?
Main question
This brings us to our main question: what are the generalization properties of biologically-plausible temporal credit assignment rules? Broadly speaking, generalization refers to a trained model’s ability to adapt to previously unseen data, which can come from held-out data or some distribution shift.
Approach
Approach using deep learning theory
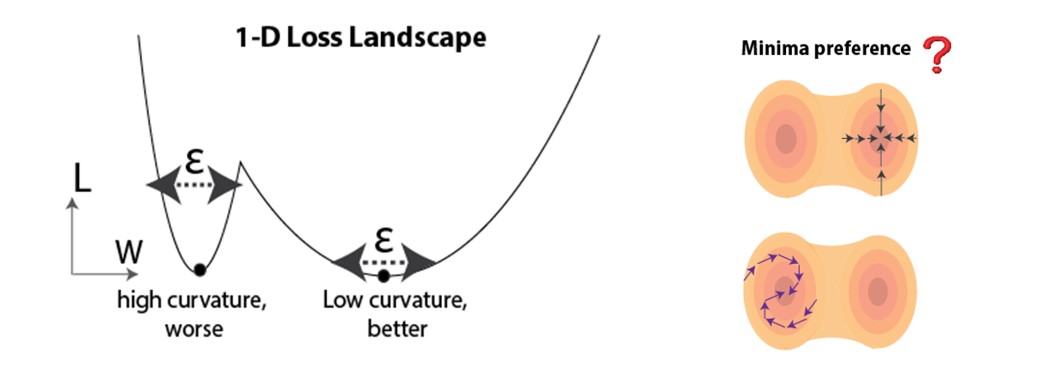
We leverage recent progress from the deep learning community: as the main theoretical tool for predicting generalization, we use loss landscape curvature at the solution point (minima in parameter space) attained from training. It has been demonstrated both empirically and theoretically that flatter minima can be more favorable for generalization [6-13]. An intuition is demonstrated in Figure 3 (left), where flatter minima are less sensitive to perturbations (e.g. noise during testing). Given that there typically exist many minima in overparameterized networks, we wonder if biologically-plausible temporal credit assignment rules systematically bias the training to converge to flatter or sharper minima (Figure 3, right).
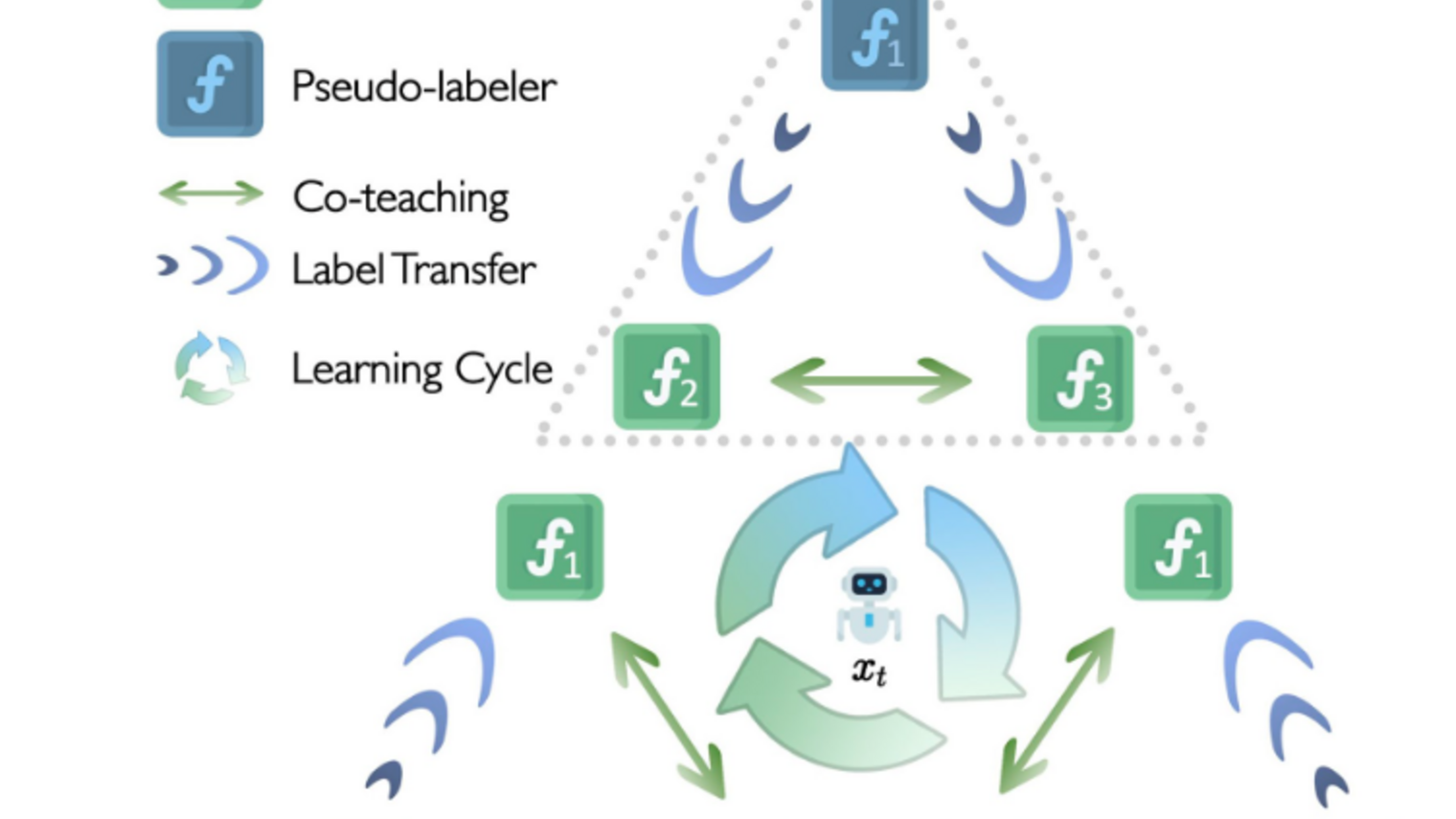
Overview of the setup
Figure 4 gives an overview of our network and learning setup. As mentioned in Introduction, we examine learning in RNNs (Figure 4, left). We compare between the standard deep learning algorithm (BPTT) as well as existing biologically-plausible temporal credit assignment rules [2-5], which have all been based on gradient truncations, as mentioned above (Figure 4, right). Please refer to the paper for details on how these algorithms work.
Findings
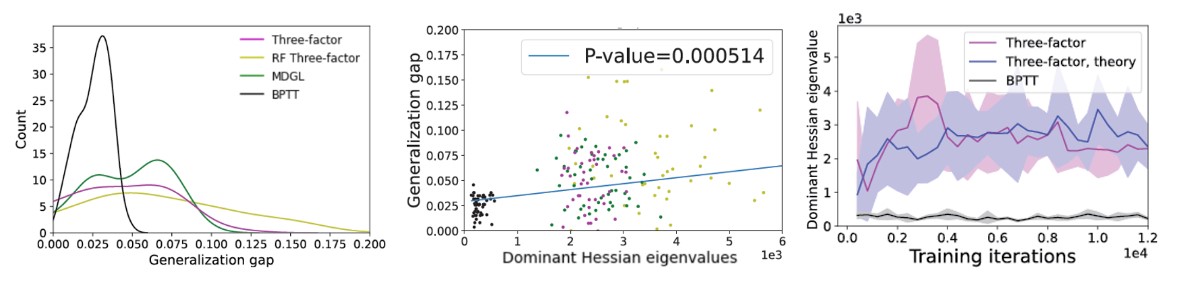
We combine theoretical analysis as well as empirical simulations across several well-known ML and neuroscience benchmarks. The main conclusion of our study is that existing biologically-plausible learning rules in RNNs attain worse generalization performance (Figure 5, left), which is consistent with their tendency to converge to high curvature regions in loss landscape (Figure 5, middle). Using dynamical systems theory, we then derived a theorem attributing the curvature convergence behavior to gradient approximation error under certain conditions (see paper). Although it has been demonstrated that noise from stochastic gradient descent can help with escaping narrow minima [7,10], the gradient approximation error due to truncation can have different properties (see paper). Our theoretical prediction matches our simulation results (Figure 5, right). We also suggested potential remedies that the brain could use to mitigate this effect.
Next steps
Our study— a stepping stone toward understanding biological generalization using deep learning methods — raises many exciting questions for future investigations at the intersection of deep learning and computational neuroscience. These questions include: (1) as the deep learning community develops better theoretical tools to study generalization, how can they be exploited to study biological learning systems? (2) How can different types of noise that appear in biological systems impact generalization? (3) How can we further leverage deep learning tools to generate testable predictions on how different biological ingredients may interact with learning rules to improve generalization?
For more information, please consult our arXiv paper [14].
References
[1] Richards et al., Nat Neurosci, 2019. [2] Murray, eLife, 2019. [3] Bellec et al., Nat Commun, 2020. [4] Liu et al., PNAS, 2021. [5] Marschall et al., JMLR, 2020. [6] Hochreiter and Schmidhuber, Neural Comput, 1997. [7] Keskar et al., ICLR, 2017. [8] Jastrezebski et al., ICLR, 2018. [9] Yao et al., NeurIPS 2019. [10] Xie et al., ICLR 2021. [11] Tsuzuku et al., ICML, 2020. [12] Petzka et al., NeurIPS, 2021. [13] Jiang et al., ICLR 2020. [14] Liu et al., NeurIPS, 2022.