Editor's Note: Published as a conference paper at ICLR 2022.
Introduction
Despite being widely used, face recognition models suffer from bias: the probability of a false positive (i.e., of an incorrect face match) strongly depends on sensitive attributes such as the ethnicity of the individual. As a result, these models can disproportionately and negatively impact minority groups, particularly when used by law enforcement.
The majority of bias reduction methods have several drawbacks: they use an end-to-end retraining approach, they may not be practical due to privacy issues, and they often reduce recognition accuracy. An alternative approach is post-processing methods that build fairer decision classifiers using the features of pre-trained models, thus avoiding the cost of retraining. However, this approach still has drawbacks: previous approaches, including AGENDA (Dhar et al, 2020), PASS (Dhar et al, 2021) and FTC (Terhörst et al, 2020), reduce accuracy, while FSN (Terhörst et al, 2021) requires tuning for different false positive rates.
In this work, we introduce the Fairness Calibration method, FairCal, which is a post-training bias reduction approach that can simultaneously:
- increase model accuracy (improving the state-of-the-art);
- produce fairly-calibrated probabilities;
- significantly reduce the gap in the false positive rates;
- avoid using knowledge of the sensitive attribute (group identity such as race, ethnicity, etc.); and
- avoid retraining, training an additional model, or further model tuning.
We apply it to the task of Face Verification, and obtain state-of-the-art results with all the above advantages. We do so by applying a post-hoc calibration method to pseudo-groups formed by unsupervised clustering.
Fairness and Bias in Face Verification
The face verification problem consists in determining whether two given images correspond to a genuine or imposter pair. An example of each case is given below:




Chouldechova (2017) showed that a maximum of two of the following three conditions can be satisfied when developing face verification solutions:
- Fairness Calibration, i.e. the solution is calibrated for each subgroup, meaning that the probability of true match is equal to the model’s confidence output.
- Predictive Equality, i.e., the solution provides equal False Positive Rates (FPRs) across different subgroups.
- Equal Opportunity, i.e., the solution provides equal False Negative Rates across different subgroups.
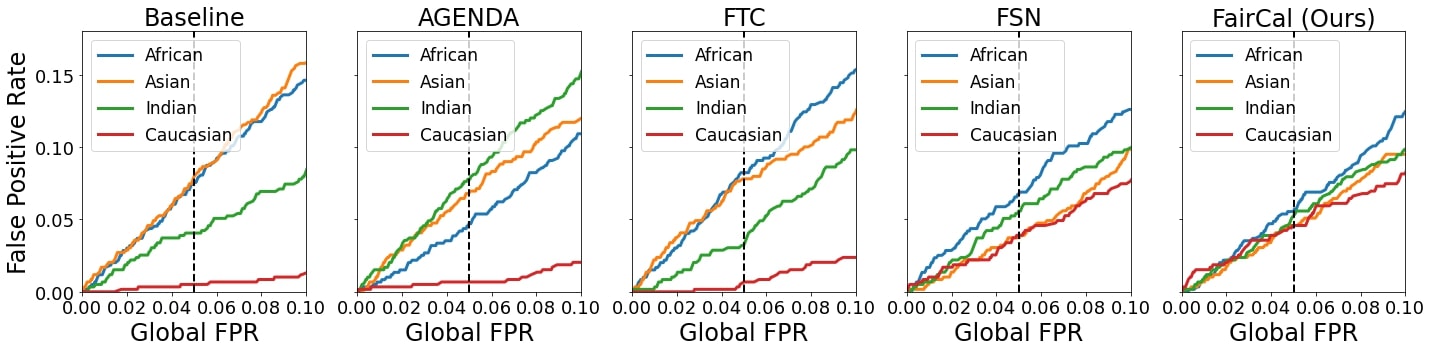
In the particular context of policing, predictive equality is considered more important than equal opportunity, as false positive errors (i.e., false arrests) risk causing significant harm, especially to members of subgroups already at disproportionate risk for police scrutiny or violence. Hence, we choose to omit equal opportunity as our goal and note that no prior method has targeted Fairness Calibration. Predictive equality is measured by comparing the FPR on each subgroup at one global FPR.
Baseline Approach
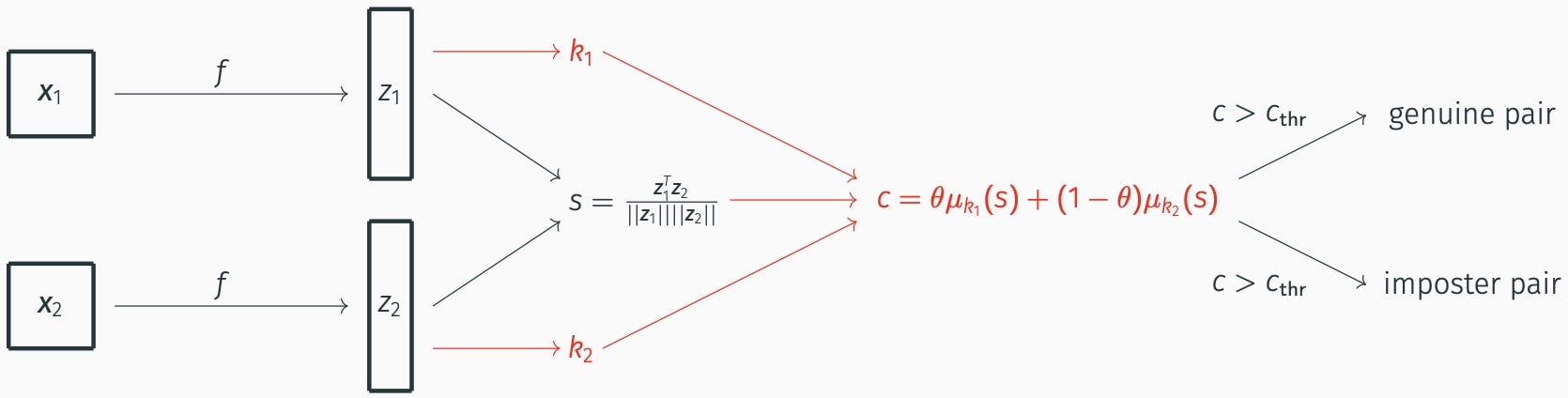
Given a trained neural network \(f\) that encodes an image \(x\) into an embedding \(z=f(x)\), the baseline classifier for the face verification problem is defined using the following steps.
- Given an image pair \((x_1, x_2)\): compute the feature embedding pair \((z_1, z_2)\).
- Compute the cosine similarity score for \((x_1, x_2)\), \(s(x_1, x_2) = \frac{z_1^T z_2}{\left\Vert z_1 \right\Vert \left\Vert z_2 \right\Vert}\).
- Given a predefined threshold \(s_{thr}\), if \(s(x_1,x_2) > s_{thr}\), then \((x_1, x_2)\) is labeled as a genuine pair.
Our approach, FairCal
We build our proposed method, FairCal, based on two main ideas:
- Use the feature vector to define population subgroups;
- Use post-hoc calibration methods that convert cosine similarity scores into probabilities of genuine (or imposter) pairs.
Calibration stage
Given a calibration set of image pairs,
- Apply the K-means algorithm to the feature embedding \(z\) of each image in the calibration set.
- Define for each cluster k an auxiliary calibration set of all image pairs where at least one belongs to cluster \(k\).
- For \(k=1,\ldots, K\) apply a post-hoc calibration to estimate the calibration map \(\mu_k\) that converts the cosine similarity scores of the pairs of images into probabilities.
For FairCal, we chose Beta Calibration (Kull et al, 2017) as the post-hoc calibration method but experiments show similar performance with other calibration methods.
Test stage
Once calibration is completed, the image pairs are tested as follows.
- Given an image pair \((x_1,x_2)\): we compute \((z_1, z_2)\) and the cluster of each image feature: \(k_1\) and \(k_2\).
- The model’s confidence \(x\) in it being a genuine pair is defined as:
\(c(x_1,x_2) = \theta \mu_{k_1} \left(s(x_1,x_2)\right) + (1-\theta) \mu_{k_2} \left(s(x_1,x_2)\right).\)
where \(\theta\) is the relative population fraction of the two clusters.
- Given a predefined threshold\(c_{thr}\), if \(c(x_1,x_2) > c_{thr}\), then \((x_1,x_2)\) is labeled as a genuine pair.
Results
Our results show that among post hoc calibration methods,
- FairCal has the best Fairness Calibration;
- FairCal has the best Predictive Equality i.e., equal FPRs;
- FairCal has the best global accuracy;
- FairCal does not require the sensitive attribute and outperforms methods that use this knowledge; and
- FairCal does not require retraining of the classifier, or any additional training.
References
Chouldechova, Alexandra. “Fair prediction with disparate impact: A study of bias in recidivism prediction instruments.” Big data 5.2 (2017): 153-163.
Dhar, Prithviraj, et al. “An adversarial learning algorithm for mitigating gender bias in face recognition.” arXiv preprint arXiv:2006.07845 2 (2020).
Dhar, Prithviraj, et al. “PASS: protected attribute suppression system for mitigating bias in face recognition.” Proceedings of the IEEE/CVF International Conference on Computer Vision. 2021.
Tim Esler. “Face Recognition Using Pytorch”. GitHub repository, accessed in July 2023, https://github.com/timesler/facenet-pytorch
Kull, Meelis, Telmo Silva Filho, and Peter Flach. “Beta calibration: A well-founded and easily implemented improvement on logistic calibration for binary classifiers.” Artificial Intelligence and Statistics. PMLR, 2017.
Terhörst, Philipp, et al. “Comparison-level mitigation of ethnic bias in face recognition.” 2020 8th international workshop on biometrics and forensics (iwbf). IEEE, 2020.
Terhörst, Philipp, et al. “Post-comparison mitigation of demographic bias in face recognition using fair score normalization.” Pattern Recognition Letters 140 (2020): 332-338.
Wang, Pingyu, et al. “Deep class-skewed learning for face recognition.” Neurocomputing 363 (2019): 35-45.
Citation
You can see the full paper here. For citations, please use the following bibtex entry:
@inproceedings{salvador2022faircal,
title={FairCal: Fairness Calibration for Face Verification},
author={Tiago Salvador and Stephanie Cairns and Vikram Voleti and Noah Marshall and Adam M Oberman},
booktitle={International Conference on Learning Representations},
year={2022},
url={https://openreview.net/forum?id=nRj0NcmSuxb}
}