Editor’s Note: Based on work published at NeurIPS 2022 and ICML 2023.
The Problem
Creating a new entity with specific characteristics is a significant part of scientific research. For instance, imagine you’re designing a robot with the goal of making it run faster.

Evaluating the performance of each design iteration, however, can be time-consuming and costly. This is why we often rely on existing datasets of various designs and their corresponding performance metrics – in this case, robot sizes and their speeds. Leveraging this static dataset to find an optimal design, a process known as offline model-based optimization, is the focus of our discussion.
Related Work and Motivation
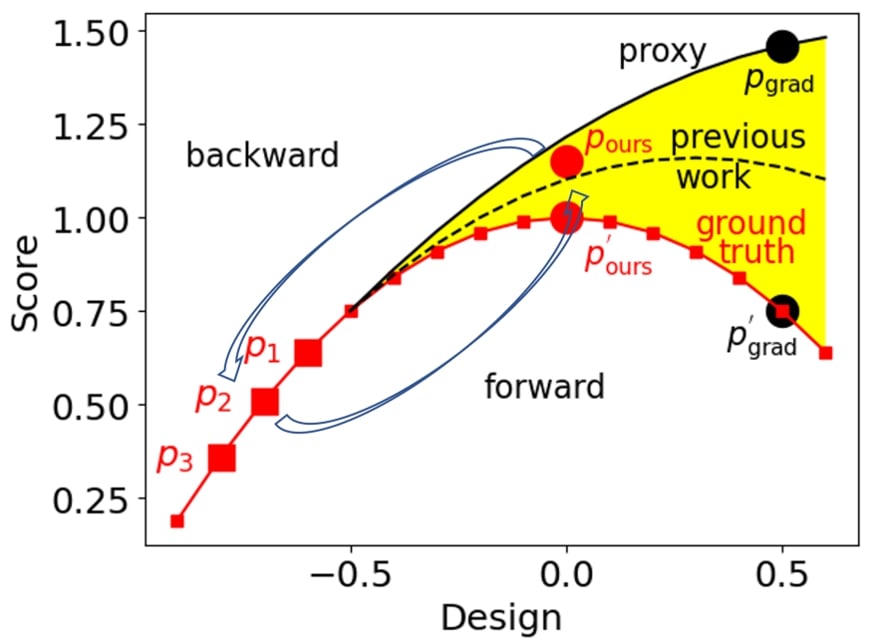
As shown above, given three robot size-speed pairs as the static dataset, a common approach is training a proxy with parameters to fit the static dataset (robot size-speed pairs). This trained proxy serves as an approximation to the ground-truth function, which predicts the robot speed based on the robot size.
After that, the optimal robot size can be obtained by optimizing the robot size to maximize the proxy function along the gradient direction . Yet, as shown above, the proxy trained on the three robot size-speed pairs overestimates the ground truth objective function, and the seemingly optimal robot size obtained by the optimization has a low robot speed .
Previous works try to better fit the proxy to the ground truth function from a model perspective and make the proxy closer to the ground-truth. Then the optimal robot size can be obtained by gradient ascent regarding the new proxy.
Bidirectional Learning
In this blog, we investigate a method that does not focus on training a better proxy closer to the ground-truth function, but instead ensures that the optimal robot size-speed pair can be used to predict the available robot size-speed pairs . As illustrated above, by ensuring the optimal robot size-speed pair can predict the available robot size-speed pairs (backward mapping) and vice versa (forward mapping), the optimal robot size-speed pair distills more information from , which makes more aligned with , leading to with a high robot speed. This approach aligns the optimal design more closely with the dataset, resulting in a more effective design.
The forward mapping and the backward mapping together align the optimal robot size-speed pair with the available robot size-speed pairs and the loss can be compactly written as:
where we aim to optimize the robot size . While this example is only for the robot design problem, also applicable to other domains.
Experimental Results
Our experimental objecives, put simply, are to create and improve various designs, with the end goal of maximizing their efficiency or performance. Here’s a breakdown of the specific goals for each experiment:
- For the Ant-like (Ant Morphology) and D’Kitty-like (D’Kitty Morphology) robots, we’re trying to find the best body shape or structure (we call it morphology) that will enable these robots to move as quickly as possible.
- In the Superconductor experiment, we’re designing materials with the goal of achieving the highest possible critical temperature, which is the temperature below which the material becomes superconducting.
- In the Hopper Controller experiment, we’re adjusting the “brain” (or neural network policy) of a hopper-style robot, which dictates its actions, with the aim of improving its overall performance.
- For the GFP experiment, we’re exploring different protein sequences to find one that produces the highest amount of fluorescence, which is a measure of how well the protein is working.
- In the TF Bind8 experiment, our aim is to find the DNA sequences that have the highest binding activity scores, meaning they’re the best at attaching to specific targets.
- Lastly, in the UTR experiment, we’re trying to identify DNA sequences that produce the highest levels of expression, which tells us how active a particular gene is.
In essence, we are trying to find the most effective designs or sequences in each of these tasks to reach the maximum potential of the subject at hand, whether it be a robot, a protein, a DNA sequence, or a superconductor. In order to evaluate the success of our experiments, we will report the ground-truth normalized score of the most promising design for each task. This score will give us a standardized measure of how well each design performs relative to the others, providing a clear metric for comparison.
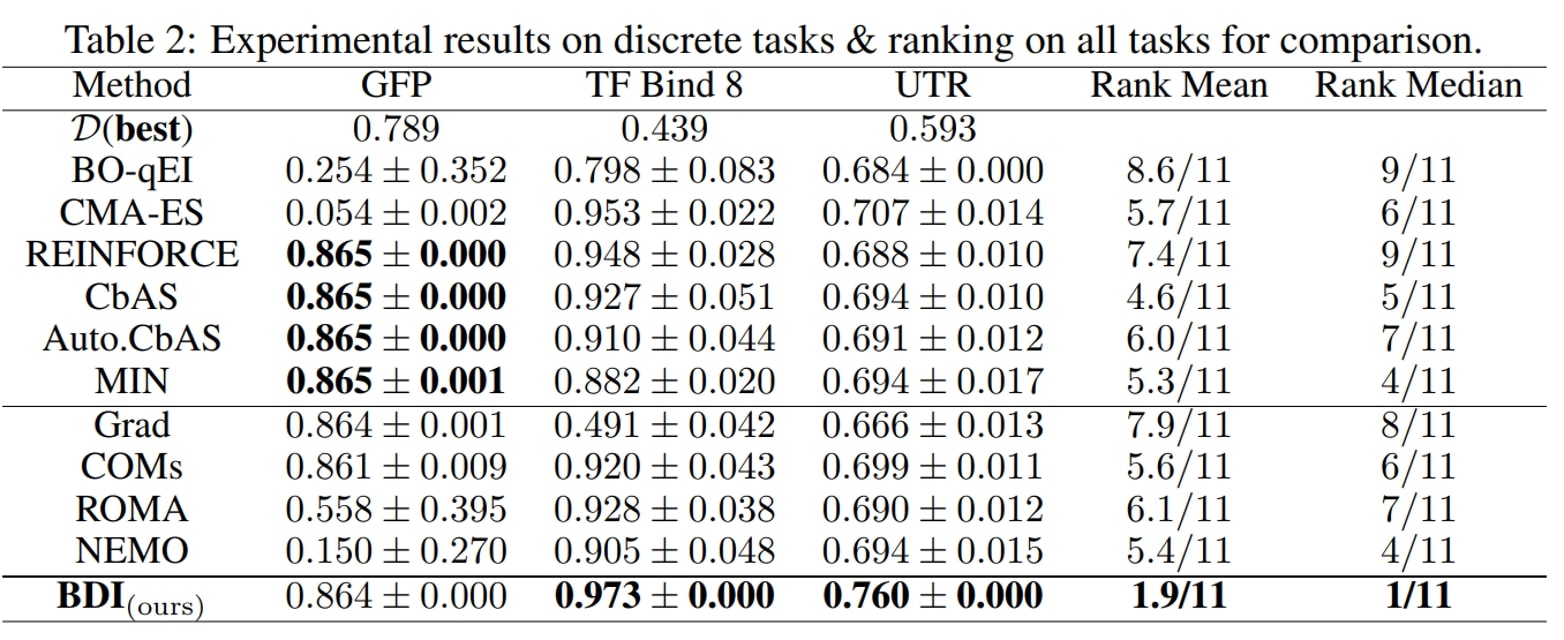
We have the following main observations:
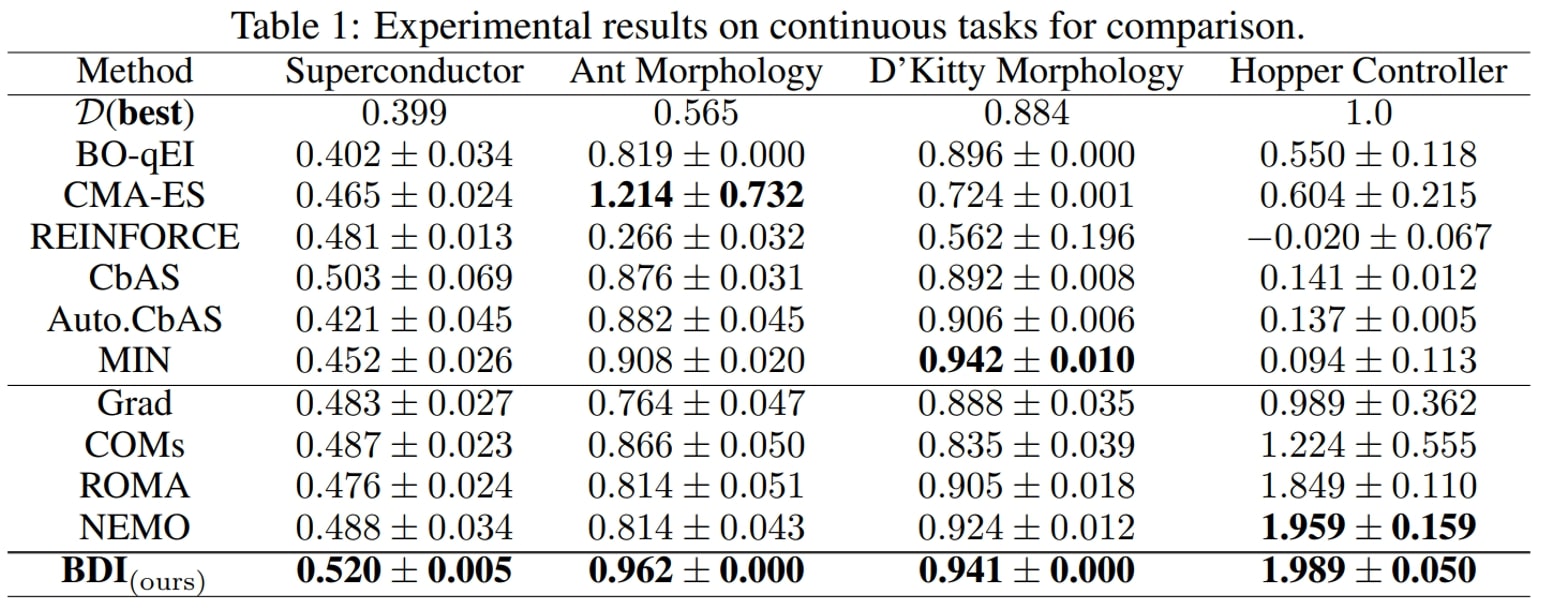
- First, BDI achieves the best result in terms of the ranking, rank mean 1.9 and rank median 1 among 11 methods, and attains the best performance on 6/7 tasks.
- Besides, compared with the naive Grad method, BDI achieves consistent gain over all four tasks. Especially in the TF Bind 8 task, BDI is much better than Grad and exceeds the Grad by 94.3% in its performance. This suggests that BDI can align the high-scoring design with the static dataset and thus mitigate the out-of-distribution problem.
- Furthermore, as for COMs, ROMA and NEMO, which all impose a prior on the DNN model, they generally perform better than Grad but worse than BDI.
- Last but not least, the generative model-based methods CbAS (0.141), Auto.CbAS (0.137) and MIN (0.094) fails on high-dimensional tasks like Hopper (D=5126) since the high-dimensional data distributions are harder to model. Compared with generative model based methods, BDI not only achieves better results but is also much simpler.
From General Design to Biological Sequence
We also integrated pre-trained Language Models (LMs) with BDI to enhance performance in tasks involving biological sequences. The new method, known as BIB, was tested on various DNA/protein sequence design tasks.
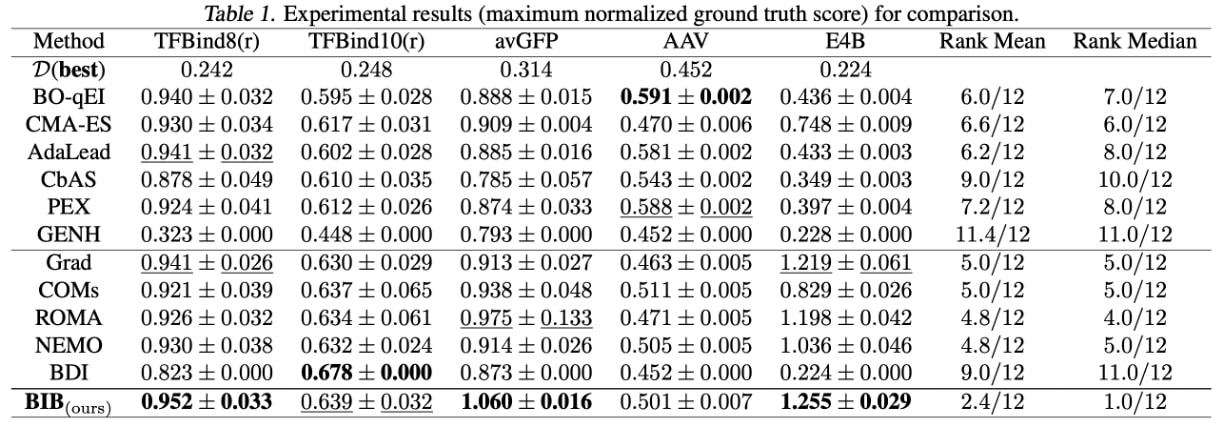
We make the following observations:
- First, BIB attains the best performance in 3 out of 5 tasks and achieves the best ranking results (rank mean 2.4/12 and rank median 1.0/12).
- Besides, BIB consistently outperforms the Grad method on all tasks: 0.952 > 0.941 in TFBind8(r), 0.639 > 0.630 in TFBind10(r), 1.060 > 0.873 in avGFP, 0.501 > 0.452 in AAV and 1.255 > 0.224 in E4B. This demonstrates that our BIB can effectively mitigate the out-of-distribution issue.
- Furthermore, BIB outperforms BDI on 4 out of 5 tasks: 0.952 > 0.823 in TFBind8(r), 0.639 < 0.678 in TFBind10(r), 1.060 > 0.913 in avGFP, 0.501 > 0.463 in AAV and 1.255 > 1.219 in E4B. This demonstrates the effectiveness of the pre-trained biological LM.
- Last but not least, the gradient-based methods are inferior for the AAV task. One possible reason is that the design space of AAV () is much smaller than those of avGFP () and E4B (), which makes the generative modeling and evolutionary algorithms more suitable.
Conclusion
BDI presents a novel and effective solution to offline model-based optimization problems. The method demonstrates the power of bidirectional learning and effectively addresses some limitations of previous techniques. Further, the incorporation of pre-trained LMs into BDI enhances the optimization of biological sequences, showing the potential of these models.