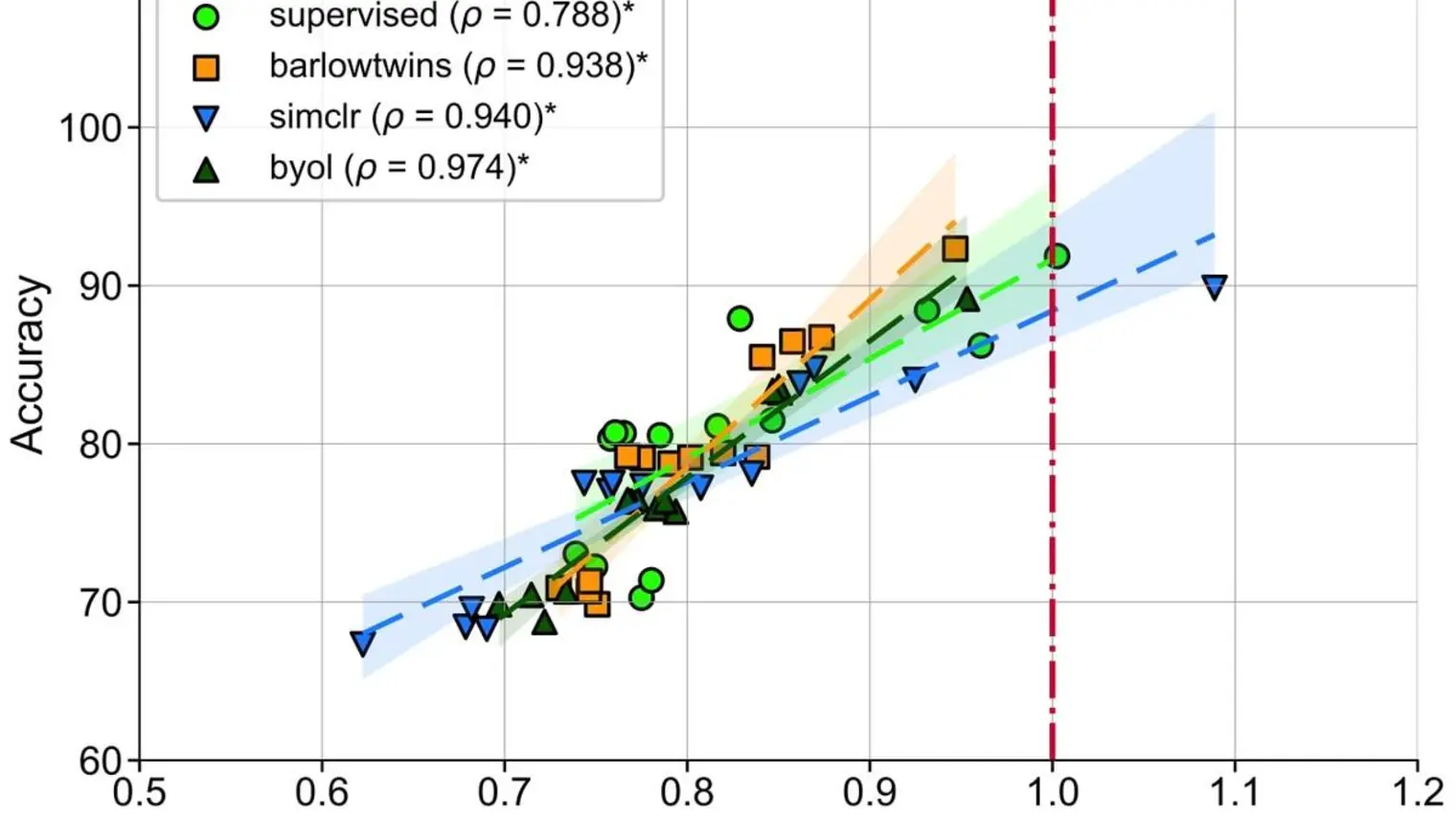
The quality of the representations learned by neural networks depends on several factors, including the loss function, learning algorithm, a
… (see more)nd model architecture. In this work, we use information geometric measures to assess the representation quality in a principled manner. We demonstrate that the sensitivity of learned representations to input perturbations, measured by the spectral norm of the feature Jacobian, provides valuable information about downstream generalization. On the other hand, measuring the coefficient of spectral decay observed in the eigen-spectrum of feature covariance provides insights into the global representation geometry. First, we empirically establish an equivalence between these notions of representation quality and show that they are inversely correlated. Second, our analysis reveals the varying roles that overparameterization plays in improving generalization. Unlike supervised learning, we observe that increasing model width leads to higher discriminability and less smoothness in the self-supervised regime. Furthermore, we report that there is no observable double descent phenomenon in SSL with non-contrastive objectives for commonly used parameterization regimes, which opens up new opportunities for tight asymptotic analysis. Taken together, our results provide a loss-aware characterization of the different role of overparam-eterization in supervised and self-supervised learning.