Editor's Note: This paper was featured as an oral presentation at NeurIPS 2023.
Mystery in Transformers and Reinforcement Learning


A reinforcement learning (RL) agent aims to maximize the sum of rewards by interacting with an environment. At each time step, the RL agent takes an action based on observed information and then receives a reward. One distinct feature of RL algorithms, in contrast to supervised learning, is their ability of (temporal) credit assignment – determining when actions that lead to a current reward occurred.
Typically, in modeling scenarios using Markov decision processes (MDPs), the assumption that the future is independent of the past given the present allows for decision-making based on current observations (i.e., state). However, real-world situations often defy this Markovian assumption, introducing partial observability. In partial observable tasks (known as POMDPs), RL agents may rely on the entire history (all previous observations and actions) to take actions. The ability to recall relevant information from history is termed (working) memory.
Therefore, solving a POMDP task necessitates two crucial forms of temporal reasoning: memory and credit assignment. These two concepts belong to the core capabilities of RL agents, despite lack of clear math definitions (which this work will cover). In the realm of deep RL, these capabilities can be simultaneously acquired by RL algorithms employing sequence models.
In recent years, Transformers, a powerful class of sequence models, have been making waves in various domains of RL, including model-free RL, model-based RL, offline RL. However, the big question remains: why are Transformers so effective in RL, especially when it comes to handling POMDPs? We’re delving into this enigma, exploring two potential game-changers: is it because Transformers learn better history representations (memory), much like their success in supervised learning? Alternatively, is it because Transformers learn a better credit assignment algorithm that outshines the known RL algorithms?
Contributions of This Work
To unravel the mysteries of Transformers in RL, our work takes a proactive approach. Firstly, we provide math definitions on memory and credit assignment. Subsequently, we apply these definitions to dissect existing tasks, many of which entangle memory and credit assignment. Finally, we evaluate Transformer-based RL in tasks that demand long-term memory and credit assignment.
Our paper’s answer to the burning question is this: Transformers excel in tasks that require long-term memory in RL, but grapple when it comes to performing long-term credit assignment.
Measuring Temporal Dependencies in RL
Formally, in POMDPs, at each time step \(t\), an agent receives the current observation \(ot\) and takes an action \(at\) based on the history \(ht=(o1:t,a1:t−1)\), based on its policy \(π(at∣ht)\). The environment, in turn, provides a reward signal \(rt\) and next observation \(ot+1\) to the agent, following the transition \(P(rt,ot+1∣ht,at)\). In addition, Q-value \(Qπ(ht,at)\) is widely used in RL to help learn the policy \(π\), defined as the expected sum of future rewards following the policy and transition.
We kick things off by introducing memory lengths in POMDPs. Each component (reward, observation, action, value) may depend on the entire history. We define memory lengths based on our intuition: How long is the minimal history required to predict / generate current reward, observation, action, or value? We’ve named these minimal history lengths as reward, transition, policy, and value memory lengths, respectively.
Next we introduce credit assignment length. Here, we ask: How long does it take for an optimal action to reap its benefits regarding its sum of n-step rewards? By definition, an optimal action is best regarding the sum of infinite-step rewards (i.e., Q-value), but we’re curious about the minimal future steps.
For formal definitions, please refer to our paper. Below we provide 2 sets of examples to better illustrate our concepts.
Example (dense vs sparse rewards). Consider two MDPs differing only in their reward function. The first MDP has a dense reward, represented by an \(ℓ_2\) distance between the current observation and the goal. Conversely, the second MDP has a sparse reward, represented by an indicator function of the goal. Given that they are MDPs, using current observation can predict every component, resulting in memory lengths of 1.
The dense-reward MDP has a short credit assignment length (around 1) because every optimal action \(a_t\) stands out in terms of immediate reward \(r_t\). The sparse-reward MDP has a long credit assignment length (around the total steps to reach the goal), because the optimal action at the first step does not stand out until the final step.
Example (opening the safe).


Scenario 1: Alice remembers her passcode set a month earlier, and opens a safe full of money. This has a policy memory length of 1 month (opening the safe by recalling the passcode seen 1 month earlier), while has a short credit assignment length.
Scenario 2: Bob picks up a key (then he can always see the key), and a month later, he opens a safe full of money. This has a short policy memory length (as he can always see the key), while has a long credit assignment length (picking up the key is only rewarded when opening the safe 1 month later).
The two scenarios provide a typical example of decoupling memory from credit assignment. Similarly, using our concepts, we can analyze prior memory and credit assignment benchmarks in RL. Please see our paper for details.
T-Mazes. To disentangle memory from credit assignment, we present two customizable toy RL tasks to be evaluated in our experiments. Both tasks are inspired by T-Maze, a classic memory task used in neuroscience. The key characteristics are:
The objective is to reach the goal G from the start S.
The goal is randomized within G1 and G2 in each episode, accessible only at oracle O.
The optimal agent first moves to O to get the goal information, and then moves right to Junction J, and finally chooses the goal.
There is a dense penalty to encourage the agent to move to J, a bonus for reaching the goal, but no reward for reaching O.
The task horizon matches the corridor length to ensure the agent can only choose the goal once.
We define Passive and Active T-Maze as follows:
Passive T-Maze: the oracle O coincides with the start S. Thus, the memory length is the full horizon (by recalling the goal information known at the beginning when choosing the goal at J), while the credit assignment is short (due to dense penalty).
Active T-Maze: the oracle O is one-step left of the start S. The memory length remains full horizon, while the credit assignment length becomes full horizon (the action of going to O is not rewarded until reaching the goal).


Evaluating Transformer-based RL on Its Memory and Credit Assignment
Let’s now delve into the assessment of memory-based RL agents leveraging Transformers. Our primary goal is to address the pivotal question at the heart of this paper: to what extent do Transformers enhance the temporal reasoning capabilities in RL?
We embrace the model-free RL architectures depicted below, employing the Transformer (GPT-2) as the sequence model, with LSTM serving as a basis for comparison. We use the full episode length as the sequence length to train the RL agents from scratch.
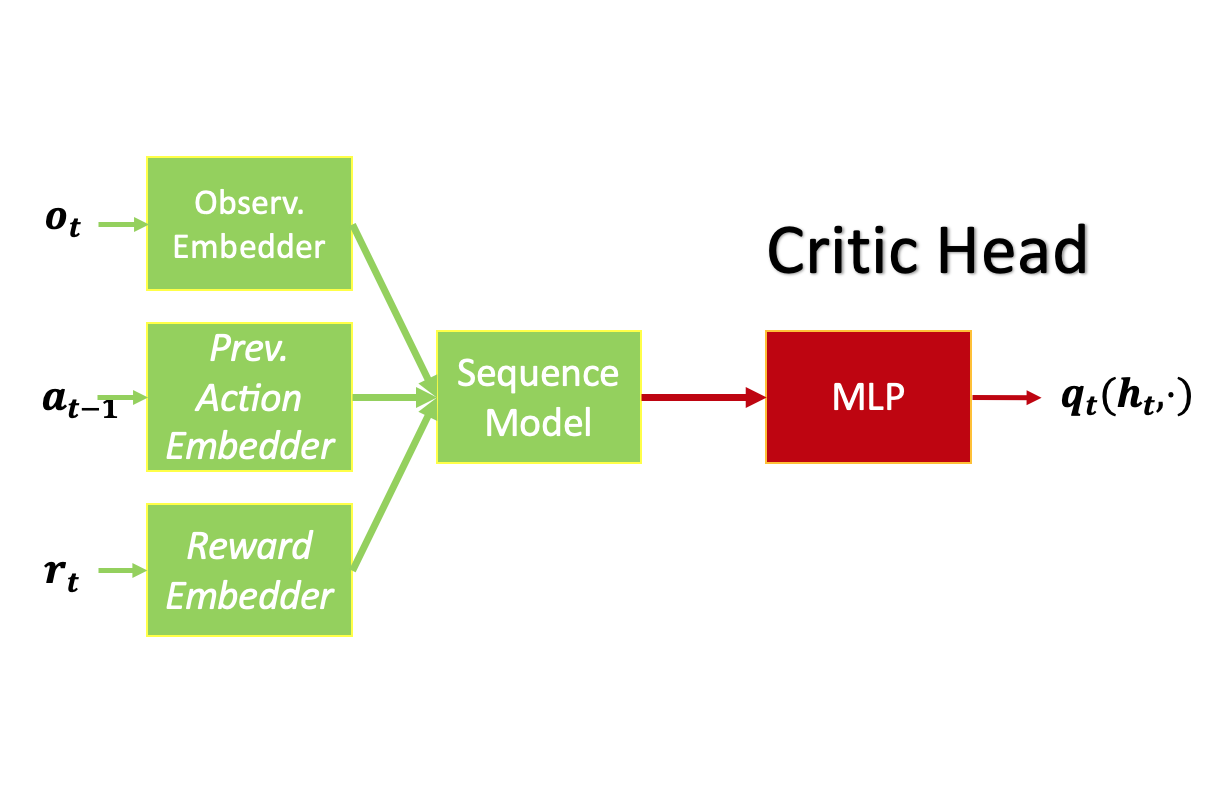
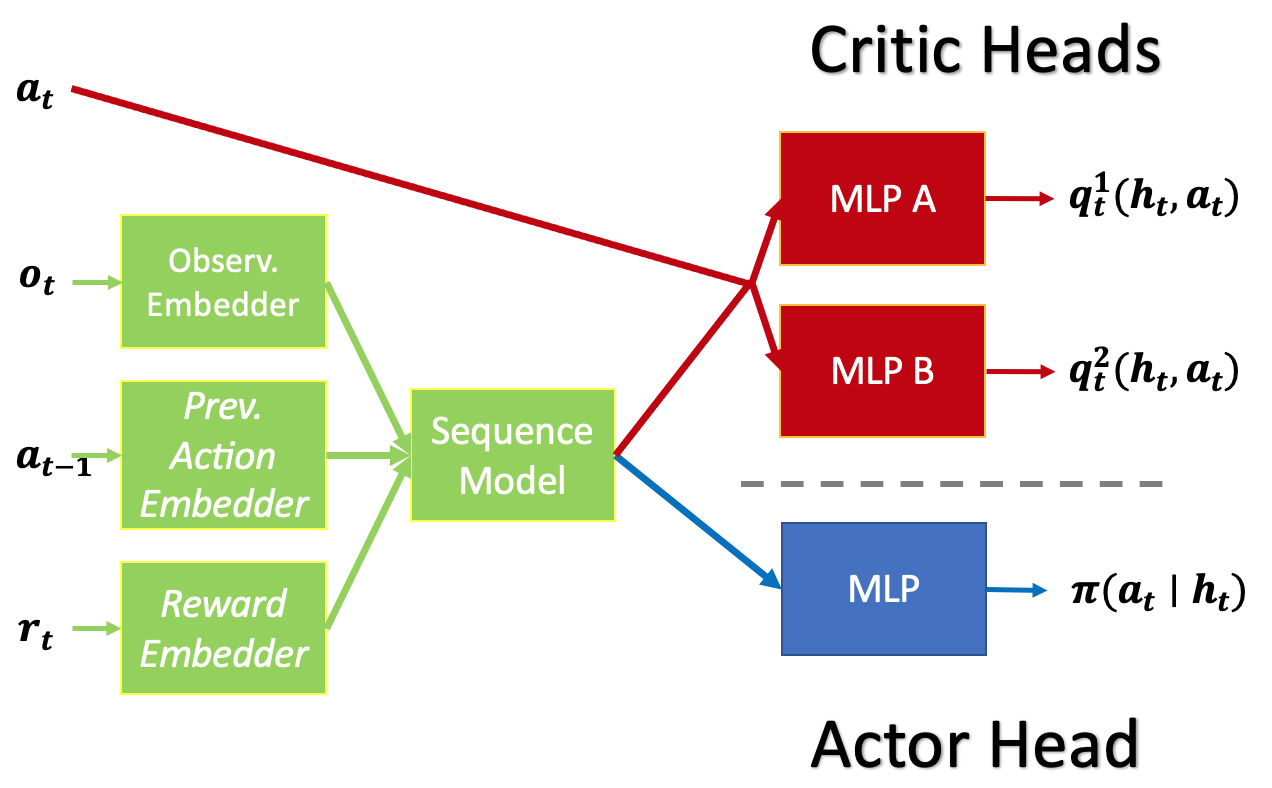
RL agent for discrete-action problems (T-Mazes) in our experiments. RL agent for continuous-action problems (PyBullet) in our experiments.
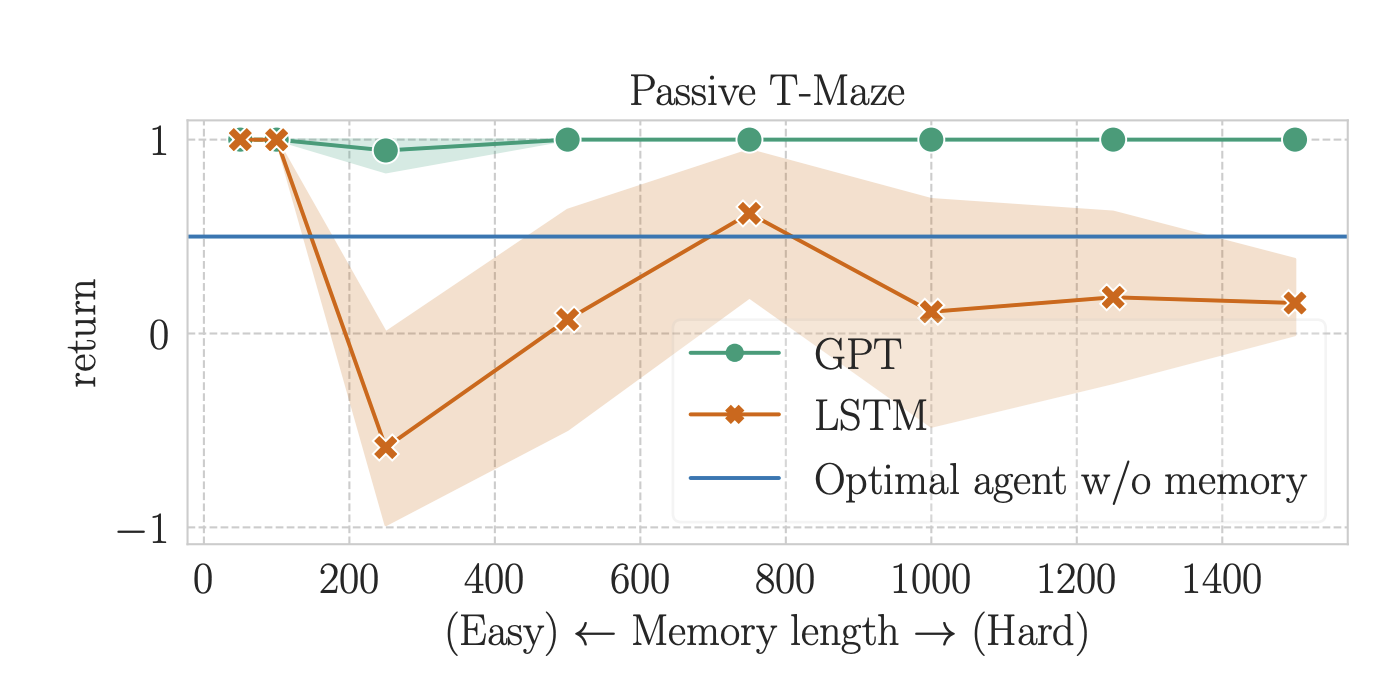
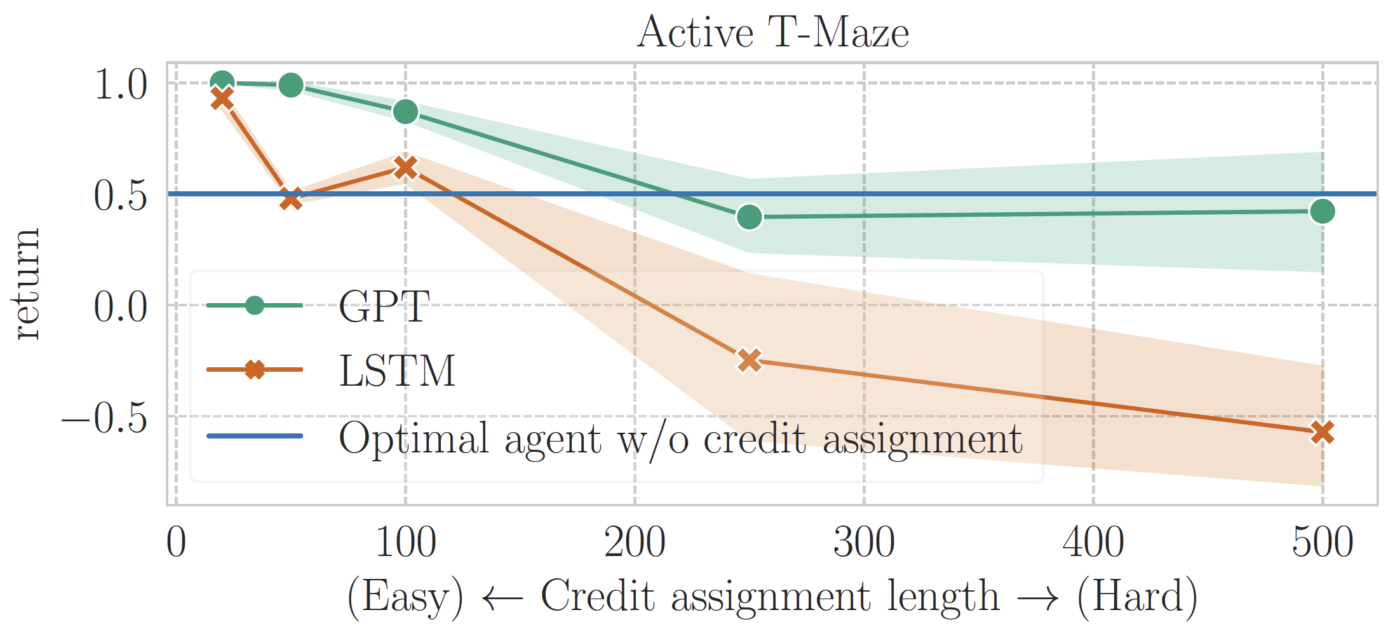
First, we evaluate memory-based RL agents on Passive and Active T-Mazes. For each task, we train each algorithm until convergence at varying lengths, ranging from 50 to 1500 in Passive T-Maze (50 to 500 in Active T-Maze).
The results, depicted in the figures below, reveal that Transformer-based RL excels in solving Passive T-Maze up to a memory length of 1500. In contrast, LSTM-based RL struggles to surpass the memoryless baseline, even with a memory length of 250—marking the longest memory length RL could solve in July 2023. Subsequent research has since extended these limits.
However, a noteworthy limitation emerges for Transformers: they prove ineffective in addressing long-term credit assignment from a length of 250 onward. This performance flaw is shared with LSTM-based RL, indicating a shared challenge in both architectures.
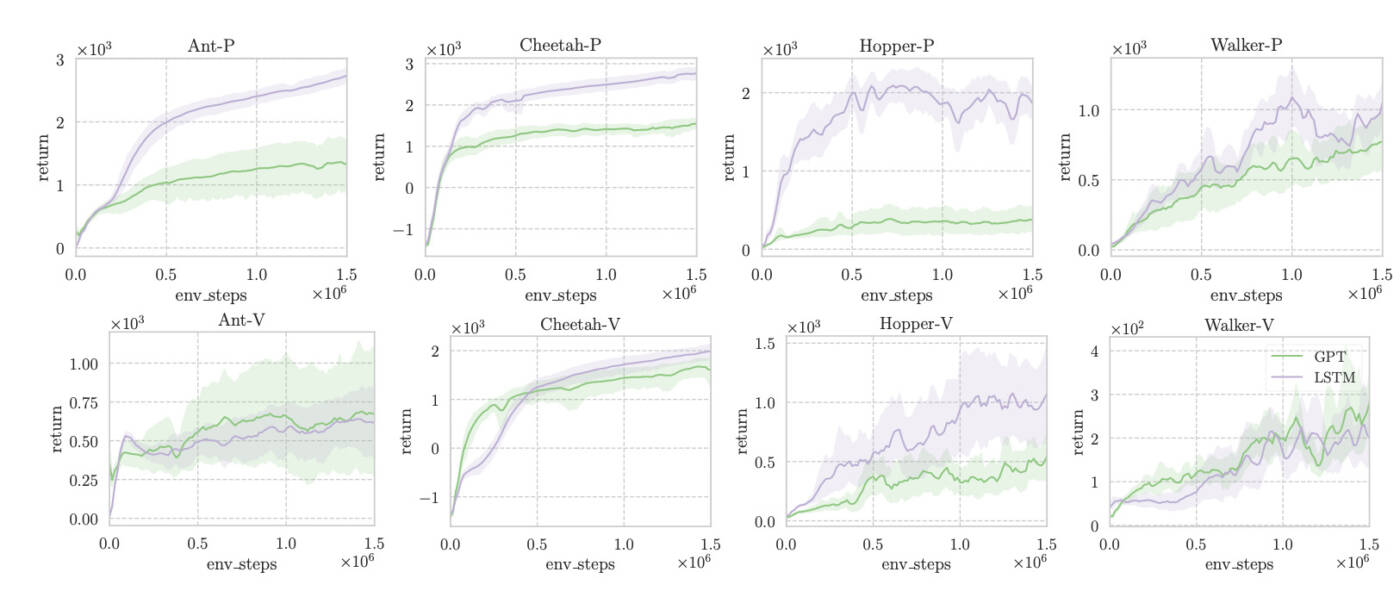
Concluding our evaluation, we assess memory-based RL on the widely used “standard POMDP” PyBullet benchmark. This benchmark features continuous control with short-term dependencies, revealing positions (-P) or velocities (-V) only to the agent. Following the prior work, we train TD3 with a context length of 64, equipped with LSTMs or GPT-2. The results show that Transformers exhibit worse sample efficiency than LSTMs across most tasks.
Links
If you’re eager to delve into the specifics of our research, please check out the arxiv version and github code
Acknowledgements
This blog is based on the collaborative work with Michel Ma, Ben Eysenbach, and Pierre-Luc Bacon. Special thanks go to Jerry Huang and Glen Berseth for their valuable assistance in editing this post.