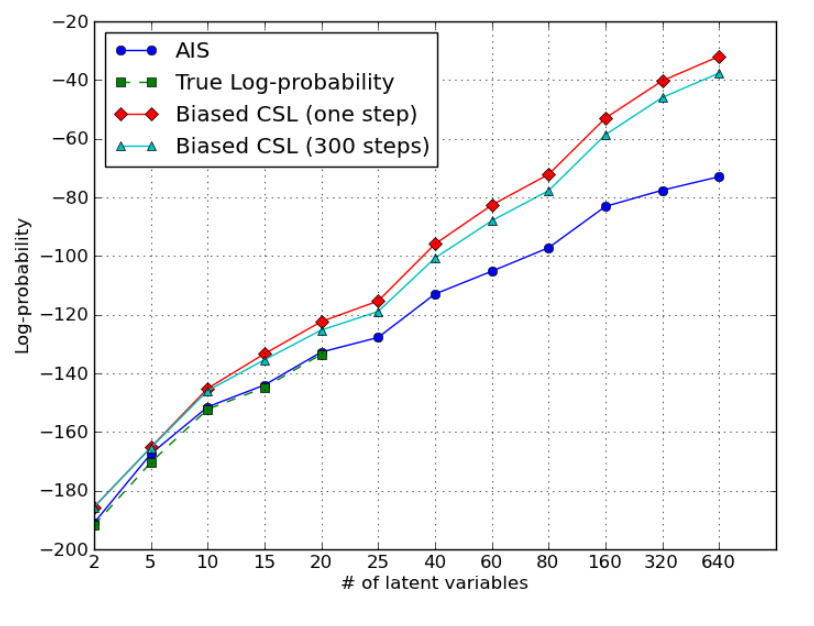
Bounding the Test Log-Likelihood of Generative Model
Plusieurs algorithmes d’apprentissage génératifs intéressants impliquent une distribution de probabilité complexe sur de nombreuses variables aléatoires, impliquant des constantes de normalisation intraitables ou une normalisation de variables latentes. Certains d’entre eux peuvent même ne pas avoir une expression analytique pour la fonction de probabilité non normalisée et aucune approximation traitable. Cela rend difficile l’estimation de la qualité de ces modèles, une fois qu’ils ont été formés, ou le suivi de leur qualité (par exemple, pour un arrêt précoce) pendant la formation. Une méthode précédemment proposée est basée sur la construction d’un estimateur de densité non paramétrique de la fonction de probabilité du modèle à partir d’échantillons générés par le modèle. Nous avons revu cette idée, proposons un estimateur plus efficace et prouvons qu’il fournit une borne inférieure à la vraie vraisemblance logarithmique du test, et un estimateur non biaisé, au fur et à mesure que le nombre d’échantillons générés va à l’infini, Malgré celui qui intègre l’effet d’un mauvais mélange (aggravation de la probabilité estimée, c’est-à-dire plus conservatrice).
Reference
Yoshua Bengio, Li Yao, Kyunghyun Cho, Bounding the Test Log-Likelihood of Generative Models, in: International Conference on Learning Representations (ICLR), 2014