On Relativistic f-Divergences
This paper provides a more rigorous look at Relativistic Generative Adversarial Networks (RGANs). We prove that the objective function of the discriminator is a statistical divergence for any concave function f with minimal properties. We also devise a few variants of relativistic f-divergences. Wasserstein GAN was originally justified by the idea that the Wasserstein distance (WD) is most sensible because it is weak (i.e., it induces a weak topology). We show that the WD is weaker than f-divergences which are weaker than relativistic f-divergences. Given the good performance of RGANs, this suggests that WGAN does not performs well primarily because of the weak metric, but rather because of regularization and the use of a relativistic discriminator.
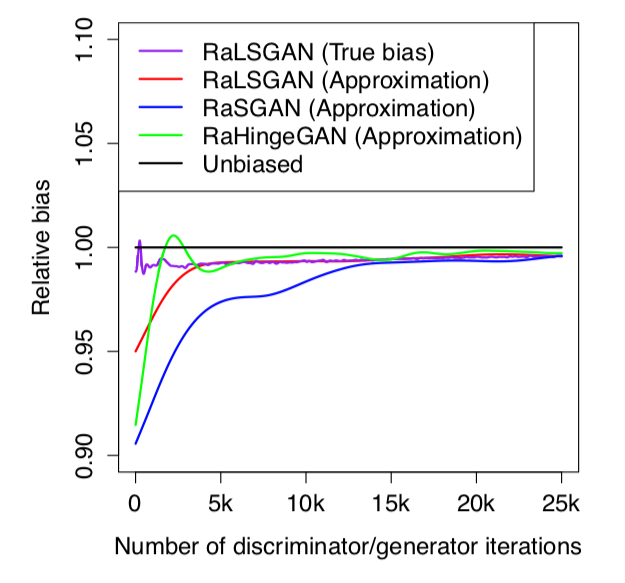
We also take a closer look at estimators of relativistic f-divergences. We introduce the minimum-variance unbiased estimator (MVUE) for Relativistic paired GANs (RpGANs; originally called RGANs which could bring confusion) and show that it does not perform better. Furthermore, we show that the estimator of Relativistic average GANs (RaGANs) is only asymptotically unbiased, but that the finitesample bias is small. Removing this bias does not improve performance.